Revizia anterioară Revizia următoare
Solutii Autumn WarmUp 2020
- Lista de probleme
- Nave Interdimensionale
- Defrisare
- Cuantictiori
Solutia problemei Nave Interdimensionale
Pentru primele 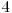 subtaskuri vezi soluţia problemei naveplanare
subtaskuri vezi soluţia problemei naveplanare
Pentru 100 de puncte vom folosi un greedy în care mutăm navele pe rând pentru a obţine o linie/coloană (liniile şi coloanele sunt de fapt independente) nouă pe care se află cel puţin o navă.
Fie![cnt[k] cnt[k]](http://www.infoarena.ro/static/images/latex/f84840677fc10b5be96e420f16d773aa_3.5pt.gif) pentru
pentru 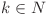 numărul de nave care trec dinspre poziţia
numărul de nave care trec dinspre poziţia  spre poziţia
spre poziţia 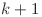 . Dacă
. Dacă ![cnt[k] cnt[k]](http://www.infoarena.ro/static/images/latex/8a5561b8a8205190bf6eb64d9b235871_3.5pt.gif) este negativ, el va reprezenta numărul de nave care trec dinspre poziţia
este negativ, el va reprezenta numărul de nave care trec dinspre poziţia 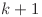 spre poziţia
spre poziţia 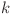 înmulţit cu
înmulţit cu 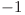 .
.
Observăm acum că costul aferent mişcării unei nave din 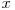 în
în  cu
cu 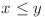 va fi numărul de valori
va fi numărul de valori 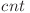 mai mari sau egale cu
mai mari sau egale cu 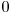 minus numărul de valori
minus numărul de valori 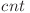 strict mai mici decât
strict mai mici decât 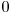 în intervalul
în intervalul ![[x,y-1] [x,y-1]](http://www.infoarena.ro/static/images/latex/7b736b7d3134b0a95e036be557879282_3.5pt.gif) .
.
De ce? Pentru că dacă ![cnt[k] cnt[k]](http://www.infoarena.ro/static/images/latex/8a5561b8a8205190bf6eb64d9b235871_3.5pt.gif) este mai mare sau egal decât
este mai mare sau egal decât 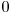 , înseamnă că trebuie să consumăm o secundă pentru a mişca nava între
, înseamnă că trebuie să consumăm o secundă pentru a mişca nava între 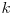 şi
şi 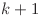 . Dacă
. Dacă ![cnt[k] cnt[k]](http://www.infoarena.ro/static/images/latex/8a5561b8a8205190bf6eb64d9b235871_3.5pt.gif) este mai mic decât
este mai mic decât 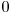 , am putea economisi o secundă: în loc să mişcăm nava asta spre dreapta, vom opri una dintre navele care se mişcă dinspre
, am putea economisi o secundă: în loc să mişcăm nava asta spre dreapta, vom opri una dintre navele care se mişcă dinspre 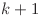 spre
spre 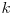 şi vom obţine acelaşi rezultat.
şi vom obţine acelaşi rezultat.
Există mai multe metode în 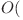 Valoarea Maximă pe care o poate lua o coordonată
Valoarea Maximă pe care o poate lua o coordonată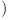 de a găsi mişcarea cea mai ieftină. Trebuie apoi să updatăm valorile din
de a găsi mişcarea cea mai ieftină. Trebuie apoi să updatăm valorile din 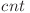 şi să reluăm algoritmul până când numărul de linii care conţin cel puţin o navă este cel dorit.
şi să reluăm algoritmul până când numărul de linii care conţin cel puţin o navă este cel dorit.
Complexitatea finală este 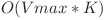
Solutia problemei Defrisare
Subtaskul 1
Cum 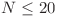 putem să folosim metoda
putem să folosim metoda 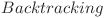 pentru a fixa direcţia în care va cădea fiecare copac.
pentru a fixa direcţia în care va cădea fiecare copac.
Subtaskul 2
Arborele are forma unui vector.
Putem să ne folosim de programarea dinamică pentru a calcula numarul optim de operaţii necesare pentru fiecare nod 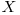 dacă acesta este orientat spre stânga sau spre dreapta.
dacă acesta este orientat spre stânga sau spre dreapta.
![DP[Nod][0] = DP[Nod][0] =](http://www.infoarena.ro/static/images/latex/f0717134a813ccc88253caf07c7fc11d_3.5pt.gif) numarul minim de operatii necesare pentru ca toti copacii aflati in stanga nodului
numarul minim de operatii necesare pentru ca toti copacii aflati in stanga nodului 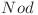 sa pice dacă acesta cade spre stânga.
sa pice dacă acesta cade spre stânga.
![DP[Nod][1] = DP[Nod][1] =](http://www.infoarena.ro/static/images/latex/5096dd1b6655bed4efc4a0c40816e0b9_3.5pt.gif) numarul minim de operatii necesare pentru ca toti copacii aflati in stanga nodului
numarul minim de operatii necesare pentru ca toti copacii aflati in stanga nodului 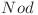 sa pice dacă acesta cade spre dreapta.
sa pice dacă acesta cade spre dreapta.
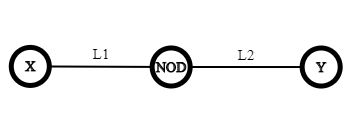
Iniţial ![DP[Nod][0] = DP[Nod][1] = min(DP[X][0], \hspace{0.1cm} DP[X][1]) + 1 DP[Nod][0] = DP[Nod][1] = min(DP[X][0], \hspace{0.1cm} DP[X][1]) + 1](http://www.infoarena.ro/static/images/latex/3623606b15a07753cc7e056a4858528c_3.5pt.gif) presupunând ca niciun copac nu are înălţimea mai mare ca
presupunând ca niciun copac nu are înălţimea mai mare ca 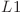 .
.
Dacă ![H[X] > L1 H[X] > L1](http://www.infoarena.ro/static/images/latex/ebe92e82f275d2c10c7a88d5f2e69d44_3.5pt.gif) înseamnă că pot să tai copacul
înseamnă că pot să tai copacul 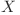 astfel încât să pice pe copacul curent, caz în care updatez
astfel încât să pice pe copacul curent, caz în care updatez ![DP[Nod][1]: DP[Nod][1]:](http://www.infoarena.ro/static/images/latex/d6c207a64d84632e1d78623d2fdc74c0_3.5pt.gif)
![DP[Nod][1] = min(DP[Nod][1], \hspace{0.1cm} DP[X][1]) DP[Nod][1] = min(DP[Nod][1], \hspace{0.1cm} DP[X][1])](http://www.infoarena.ro/static/images/latex/30fd9022c0481ebd7d1ae05fa7717ecc_3.5pt.gif)
Dacă ![H[Nod] > L1 H[Nod] > L1](http://www.infoarena.ro/static/images/latex/49399ad780a1b2c38166bcb6287d3244_3.5pt.gif) înseamnă că pot să tai copacul curent astfel încât să pice pe copacul
înseamnă că pot să tai copacul curent astfel încât să pice pe copacul 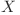 , caz în care updatez
, caz în care updatez ![DP[Nod][0]: DP[Nod][0]:](http://www.infoarena.ro/static/images/latex/8ab2c5bf62e557913092126bb37554f8_3.5pt.gif)
![DP[Nod][0] = min(DP[Nod][0], \hspace{0.1cm} DP[X][0]) DP[Nod][0] = min(DP[Nod][0], \hspace{0.1cm} DP[X][0])](http://www.infoarena.ro/static/images/latex/30f28e5bc9ce905d45862ece96748680_3.5pt.gif)
Subtaskul 3
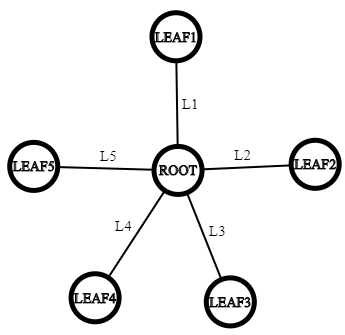
Pentru acest subtask există 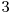 cazuri:
cazuri:
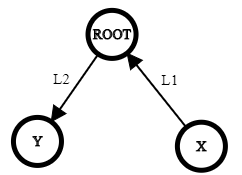
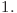 Există două noduri
Există două noduri 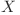 şi
şi 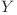 legate de radacină prin muchii de lungimi
legate de radacină prin muchii de lungimi 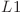 , respectiv
, respectiv 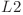 astfel încât
astfel încât ![H[x] > L1 H[x] > L1](http://www.infoarena.ro/static/images/latex/90c3f3285e07ddbc310d77e1bfe36046_3.5pt.gif) şi
şi ![H[radacina] > L2 H[radacina] > L2](http://www.infoarena.ro/static/images/latex/a07d574031ca19b24046f009fe71a482_3.5pt.gif) . Răspunsul este
. Răspunsul este 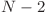 .
.
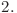 Există un nod
Există un nod 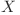 legat de radacină printr-o muchie de lungime
legat de radacină printr-o muchie de lungime 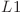 astfel încât
astfel încât ![H[radacina] > L1 H[radacina] > L1](http://www.infoarena.ro/static/images/latex/e114e999366e6c7a38dfa152f4a433b5_3.5pt.gif) sau
sau ![H[X] > L1 H[X] > L1](http://www.infoarena.ro/static/images/latex/bd6481c4ed9c15817ae3e0795a32c1c0_3.5pt.gif) . Răspunsul este
. Răspunsul este 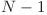 .
.
 Nu există nicio muchie a cărei lungimi este mai mică decât înălţimea unuia dintre copacii pe care îi leagă. Răspunsul este
Nu există nicio muchie a cărei lungimi este mai mică decât înălţimea unuia dintre copacii pe care îi leagă. Răspunsul este  .
.
Subtaskul 4
Pentru a rezolva acest subtask vom folosi o abordare similară cu cea de la subtaskul 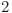 .
.
Definim:
![DP[Nod][0] = DP[Nod][0] =](http://www.infoarena.ro/static/images/latex/afda9d996fb9c94504cf809e0da3b07f_3.5pt.gif) numărul minim de operaţii necesare pentru a rezolva subarborele nodului
numărul minim de operaţii necesare pentru a rezolva subarborele nodului 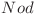 dacă acesta cade spre unul dintre fii şi nu este doborât de alt fiu.
dacă acesta cade spre unul dintre fii şi nu este doborât de alt fiu.
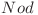 poate să nu atingă niciun alt copac.
poate să nu atingă niciun alt copac.
![DP[Nod][1] = DP[Nod][1] =](http://www.infoarena.ro/static/images/latex/c179d1d1b2ed9a5d1aa8424bd3b3b07b_3.5pt.gif) numărul minim de operaţii necesare pentru a rezolva subarborele nodului
numărul minim de operaţii necesare pentru a rezolva subarborele nodului 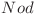 dacă acesta cade spre unul dintre fii şi este doborât de alt fiu
dacă acesta cade spre unul dintre fii şi este doborât de alt fiu
![DP[Nod][2] = DP[Nod][2] =](http://www.infoarena.ro/static/images/latex/029956abf468e2b354621b1ced42d6c4_3.5pt.gif) numărul minim de operaţii necesare pentru a rezolva subarborele nodului
numărul minim de operaţii necesare pentru a rezolva subarborele nodului 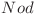 dacă acesta cade spre radacină.
dacă acesta cade spre radacină.
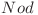 poate să nu fie atins de niciun alt copac.
poate să nu fie atins de niciun alt copac.
![BEST[Nod] = min(DP[Nod][0], \hspace{0.1cm} DP[Nod][1], \hspace{0.1cm} DP[Nod][2]) BEST[Nod] = min(DP[Nod][0], \hspace{0.1cm} DP[Nod][1], \hspace{0.1cm} DP[Nod][2])](http://www.infoarena.ro/static/images/latex/71929015a2e19ac9b5a6299febf4c9a6_3.5pt.gif)
Rădăcina poate să fie orice nod cu grad mai mic sau egal cu 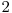 .
.
Să presupunem că ne aflăm în nodul 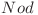 cu fii
cu fii 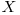 şi
şi 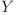 de care se leagă prin muchiile de lungime
de care se leagă prin muchiile de lungime 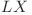 respectiv
respectiv 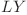 .
.
Iniţializăm ![DP[Nod][0], \hspace{0.1cm} DP[Nod][1], \hspace{0.1cm} DP[Nod][2] DP[Nod][0], \hspace{0.1cm} DP[Nod][1], \hspace{0.1cm} DP[Nod][2]](http://www.infoarena.ro/static/images/latex/1f40e6e578b789d0ca82608d02e35f11_3.5pt.gif) cu
cu ![1 + BEST[X] + BEST[Y] 1 + BEST[X] + BEST[Y]](http://www.infoarena.ro/static/images/latex/a7d4cd8c2bd7d047460c060a8f1b108c_3.5pt.gif) caz în care tai copacul curent fără să afecteze/ să fie afectat de subarborii lui
caz în care tai copacul curent fără să afecteze/ să fie afectat de subarborii lui 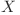 şi
şi 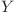 .
.
Dacă 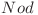 poate să doboare copacul
poate să doboare copacul 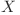 atunci updatez
atunci updatez ![DP[Nod][0] : DP[Nod][0] = min(DP[Nod][0], \hspace{0.1cm} DP[X][0] + BEST[Y]) DP[Nod][0] : DP[Nod][0] = min(DP[Nod][0], \hspace{0.1cm} DP[X][0] + BEST[Y])](http://www.infoarena.ro/static/images/latex/540286fe626173f1427db08cd58d29ba_3.5pt.gif) . Analog pentru
. Analog pentru 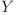 .
.
Dacă 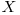 poate să doboare copacul curent atunci updatez
poate să doboare copacul curent atunci updatez ![DP[Nod][2] : DP[Nod][2] = min(DP[Nod][2], \hspace{0.1cm} DP[X][2] + BEST[Y]) DP[Nod][2] : DP[Nod][2] = min(DP[Nod][2], \hspace{0.1cm} DP[X][2] + BEST[Y])](http://www.infoarena.ro/static/images/latex/9599ca070baa3cc4c6259d71271c3f0e_3.5pt.gif) . Analog pentru
. Analog pentru 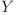 .
.
Dacă 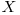 poate sa doboare copacul curent şi
poate sa doboare copacul curent şi 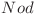 poate să doboare copacul
poate să doboare copacul 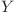 atunci updatez
atunci updatez ![DP[Nod][1] : DP[Nod][1] = min(DP[Nod][1], \hspace{0.1cm} DP[X][2] + DP[Y][0] - 1) DP[Nod][1] : DP[Nod][1] = min(DP[Nod][1], \hspace{0.1cm} DP[X][2] + DP[Y][0] - 1)](http://www.infoarena.ro/static/images/latex/14c5f06a8498877851ca27db8c067439_3.5pt.gif) . Deoarece unesc două lanţuri numarul de operaţii necesare se micşorează cu 1. Analog pentru cazul
. Deoarece unesc două lanţuri numarul de operaţii necesare se micşorează cu 1. Analog pentru cazul 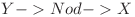 .
.
Subtaskul 5
Soluţia se bazeaza pe acelaşi 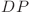 ca la subtaskul 4.
ca la subtaskul 4.
Pentru fiecare nod o să avem nevoie de o variabilă în care reţinem ![\sum_{fiu \in Nod} BEST[fiu] \sum_{fiu \in Nod} BEST[fiu]](http://www.infoarena.ro/static/images/latex/948753fbaa266004fa4bba50c84b2cce_5.36115pt.gif) .
.
![DP[Nod][0] DP[Nod][0]](http://www.infoarena.ro/static/images/latex/735d52f1412899b3f4b0152bd99fb378_3.5pt.gif) şi
şi ![DP[Nod][2] DP[Nod][2]](http://www.infoarena.ro/static/images/latex/ee408f2738250e477cd993f80338a231_3.5pt.gif) se calculează similar.
se calculează similar.
Pentru a calcula ![DP[Nod][1] DP[Nod][1]](http://www.infoarena.ro/static/images/latex/b8aabc3ddcaf8bf795655c9c5c500d79_3.5pt.gif) încercăm să cuplăm nodul curent cu fiecare fiu
încercăm să cuplăm nodul curent cu fiecare fiu 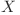 pe rând considerând că
pe rând considerând că 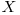 este doborât de copacul curent.
este doborât de copacul curent.
Avem însă nevoie să ştim ce fiu e optim să considerăm că doboară copacul 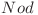 .
.
Să presupunem că exista doi fii 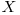 şi
şi 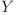 care pot să cadă spre nodul actual. Considerăm că
care pot să cadă spre nodul actual. Considerăm că 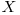 este mai bun ca
este mai bun ca 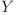 dacă
dacă ![DP[X][2] - BEST[X] < DP[Y][2] - BEST[Y]
DP[X][2] - BEST[X] < DP[Y][2] - BEST[Y]](http://www.infoarena.ro/static/images/latex/8905f184a3b156b991775497ef4c32c9_3.5pt.gif) . Astfel avem nevoie doar de primele două cele mai bune noduri care pot fi determinate printr-o singură parcurgere a fiilor nodului actual.
. Astfel avem nevoie doar de primele două cele mai bune noduri care pot fi determinate printr-o singură parcurgere a fiilor nodului actual.
Solutia problemei Cuantictiori
 Se asigură că se poate demonstra că numărul de progresii geometrice de lungime
Se asigură că se poate demonstra că numărul de progresii geometrice de lungime  care au prima valoare egală cu
care au prima valoare egală cu 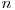 este egal cu cel mai mare număr natural
este egal cu cel mai mare număr natural 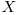 cu proprietatea că
cu proprietatea că 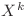 este divizor al lui
este divizor al lui  .
.
Pentru demonstraţie vedeţi soluţia problemei nambartiori.
Fie  cel mai mare divizor comun al exponenţilor din descompunerea în factori primi a lui
cel mai mare divizor comun al exponenţilor din descompunerea în factori primi a lui  .
.
Vom demonstra mai întai că dacă 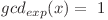 , atunci
, atunci 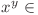 cu
cu 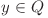 numai dacă
numai dacă 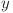 se află de asemenea şi în
se află de asemenea şi în 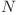 . (Lema 1)
. (Lema 1)
Fie 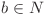 astfel încât
astfel încât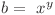 şi
şi 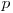 şi
şi 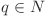 cu proprietatea că
cu proprietatea că 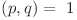 , astfel încât
, astfel încât 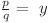 .
.
Atunci 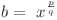 şi deci
şi deci 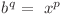 .
.
Dacă 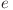 şi
şi 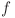 sunt exponenţii factorului prim
sunt exponenţii factorului prim 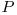 din descompunerea în factori primi a numerelor
din descompunerea în factori primi a numerelor 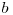 şi respectiv
şi respectiv  , reiese că:
, reiese că: 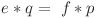 .
.
Ştim că 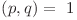 , deci
, deci 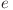 va trebui să fie divizibil cu
va trebui să fie divizibil cu 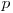 şi
şi 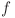 va trebui să fie divizibil cu
va trebui să fie divizibil cu 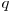 .
.
Ştiind că acest lucru se aplică pentru orice număr prim 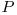 , putem deci spune că toţi exponenţii din descompunerea în factori primi a numărului
, putem deci spune că toţi exponenţii din descompunerea în factori primi a numărului  vor fi divizibili cu
vor fi divizibili cu 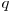 .
.
Deci cel mai mare divizor comun al exponenţilor din descompunerea în factori primi a numărului  va fi divizibil cu
va fi divizibil cu 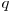 .
.
Din moment ce 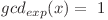 , va trebui ca şi
, va trebui ca şi 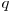 să fie egal cu
să fie egal cu  .
.
Atunci  , ceea ce trebuia demonstrat.
, ceea ce trebuia demonstrat.
Dacă 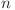 este primul termen,
este primul termen, 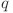 este raţia şi progresia cuantică are lungimea
este raţia şi progresia cuantică are lungimea 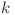 , condiţia de existenţă este următoarea:
, condiţia de existenţă este următoarea:
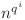 este natural pentru oricare
este natural pentru oricare 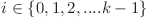 .
.
Fie 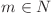 astfel încât
astfel încât 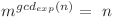 . Intuitiv,
. Intuitiv, 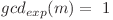 . Înlocuind mai sus, obţinem:
. Înlocuind mai sus, obţinem:
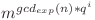 este natural pentru oricare
este natural pentru oricare 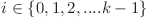 .
.
Folosing Lema 1, obţinem că:
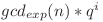 este natural pentru oricare
este natural pentru oricare 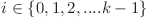 .
.
Observăm astfel că am ajuns la problema nambartiori, doar că aplicata valorii 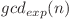 .
.
Subtaskul 2
Putem să trecem prin fiecare numar, să-i calculam  -ul si să-i aplicam functia din nambartiori ca apoi să-l adaugam la rezultat.
-ul si să-i aplicam functia din nambartiori ca apoi să-l adaugam la rezultat.
Subtaskul 3
Observăm că un numar 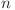 ne interesează doar dacă
ne interesează doar dacă 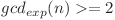 . Asta înseamnă că în loc să trecem prin toate numerele pana la
. Asta înseamnă că în loc să trecem prin toate numerele pana la 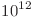 , putem pur şi simplu să mergem prin bazele acestor numere până în
, putem pur şi simplu să mergem prin bazele acestor numere până în 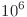 . Prin baze ne referim la numerele
. Prin baze ne referim la numerele 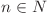 cu proprietatea că
cu proprietatea că 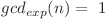 .
.
