Solutia problemei Defrisare
Subtaskul 1
Cum 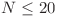 putem să folosim metoda
putem să folosim metoda 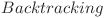 pentru a fixa direcţia în care va cădea fiecare copac.
pentru a fixa direcţia în care va cădea fiecare copac.
Subtaskul 2
Arborele are forma unui vector.
Putem să ne folosim de programarea dinamică pentru a calcula numarul optim de operaţii necesare pentru fiecare nod 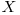 dacă acesta este orientat spre stânga sau spre dreapta.
dacă acesta este orientat spre stânga sau spre dreapta.
![DP[Nod][0] = DP[Nod][0] =](http://www.infoarena.ro/static/images/latex/f0717134a813ccc88253caf07c7fc11d_3.5pt.gif) numarul minim de operatii necesare pentru ca toti copacii aflati in stanga nodului
numarul minim de operatii necesare pentru ca toti copacii aflati in stanga nodului 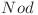 sa pice dacă acesta cade spre stânga.
sa pice dacă acesta cade spre stânga.
![DP[Nod][1] = DP[Nod][1] =](http://www.infoarena.ro/static/images/latex/5096dd1b6655bed4efc4a0c40816e0b9_3.5pt.gif) numarul minim de operatii necesare pentru ca toti copacii aflati in stanga nodului
numarul minim de operatii necesare pentru ca toti copacii aflati in stanga nodului 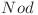 sa pice dacă acesta cade spre dreapta.
sa pice dacă acesta cade spre dreapta.
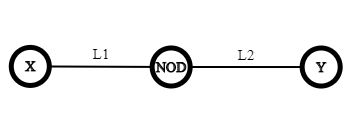
Iniţial ![DP[Nod][0] = DP[Nod][1] = min(DP[X][0], \hspace{0.1cm} DP[X][1]) + 1 DP[Nod][0] = DP[Nod][1] = min(DP[X][0], \hspace{0.1cm} DP[X][1]) + 1](http://www.infoarena.ro/static/images/latex/3623606b15a07753cc7e056a4858528c_3.5pt.gif) presupunând ca niciun copac nu are înălţimea mai mare ca
presupunând ca niciun copac nu are înălţimea mai mare ca 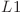 .
.
Dacă ![H[X] > L1 H[X] > L1](http://www.infoarena.ro/static/images/latex/ebe92e82f275d2c10c7a88d5f2e69d44_3.5pt.gif) înseamnă că pot să tai copacul
înseamnă că pot să tai copacul 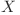 astfel încât să pice pe copacul curent, caz în care updatez
astfel încât să pice pe copacul curent, caz în care updatez ![DP[Nod][1]: DP[Nod][1]:](http://www.infoarena.ro/static/images/latex/d6c207a64d84632e1d78623d2fdc74c0_3.5pt.gif)
![DP[Nod][1] = min(DP[Nod][1], \hspace{0.1cm} DP[X][1]) DP[Nod][1] = min(DP[Nod][1], \hspace{0.1cm} DP[X][1])](http://www.infoarena.ro/static/images/latex/30fd9022c0481ebd7d1ae05fa7717ecc_3.5pt.gif)
Dacă ![H[Nod] > L1 H[Nod] > L1](http://www.infoarena.ro/static/images/latex/49399ad780a1b2c38166bcb6287d3244_3.5pt.gif) înseamnă că pot să tai copacul curent astfel încât să pice pe copacul
înseamnă că pot să tai copacul curent astfel încât să pice pe copacul 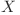 , caz în care updatez
, caz în care updatez ![DP[Nod][0]: DP[Nod][0]:](http://www.infoarena.ro/static/images/latex/8ab2c5bf62e557913092126bb37554f8_3.5pt.gif)
![DP[Nod][0] = min(DP[Nod][0], \hspace{0.1cm} DP[X][0]) DP[Nod][0] = min(DP[Nod][0], \hspace{0.1cm} DP[X][0])](http://www.infoarena.ro/static/images/latex/30f28e5bc9ce905d45862ece96748680_3.5pt.gif)
Subtaskul 3
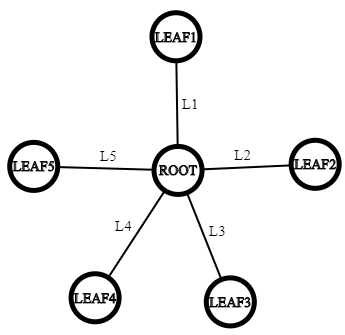
Pentru acest subtask există 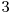 cazuri:
cazuri:
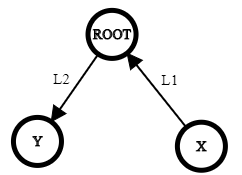
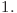 Există două noduri
Există două noduri 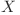 şi
şi 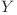 legate de radacină prin muchii de lungimi
legate de radacină prin muchii de lungimi 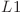 , respectiv
, respectiv 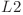 astfel încât
astfel încât ![H[x] > L1 H[x] > L1](http://www.infoarena.ro/static/images/latex/90c3f3285e07ddbc310d77e1bfe36046_3.5pt.gif) şi
şi ![H[radacina] > L2 H[radacina] > L2](http://www.infoarena.ro/static/images/latex/a07d574031ca19b24046f009fe71a482_3.5pt.gif) . Răspunsul este
. Răspunsul este 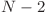 .
.
 Există un nod
Există un nod 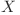 legat de radacină printr-o muchie de lungime
legat de radacină printr-o muchie de lungime 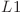 astfel încât
astfel încât ![H[radacina] > L1 H[radacina] > L1](http://www.infoarena.ro/static/images/latex/e114e999366e6c7a38dfa152f4a433b5_3.5pt.gif) sau
sau ![H[X] > L1 H[X] > L1](http://www.infoarena.ro/static/images/latex/bd6481c4ed9c15817ae3e0795a32c1c0_3.5pt.gif) . Răspunsul este
. Răspunsul este 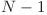 .
.
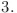 Nu există nicio muchie a cărei lungimi este mai mică decât înălţimea unuia dintre copacii pe care îi leagă. Răspunsul este
Nu există nicio muchie a cărei lungimi este mai mică decât înălţimea unuia dintre copacii pe care îi leagă. Răspunsul este  .
.
Subtaskul 4
Pentru a rezolva acest subtask vom folosi o abordare similară cu cea de la subtaskul 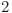 .
.
Definim:
![DP[Nod][0] = DP[Nod][0] =](http://www.infoarena.ro/static/images/latex/afda9d996fb9c94504cf809e0da3b07f_3.5pt.gif) numărul minim de operaţii necesare pentru a rezolva subarborele nodului
numărul minim de operaţii necesare pentru a rezolva subarborele nodului 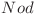 dacă acesta cade spre unul dintre fii şi nu este doborât de alt fiu.
dacă acesta cade spre unul dintre fii şi nu este doborât de alt fiu.
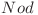 poate să nu atingă niciun alt copac.
poate să nu atingă niciun alt copac.
![DP[Nod][1] = DP[Nod][1] =](http://www.infoarena.ro/static/images/latex/c179d1d1b2ed9a5d1aa8424bd3b3b07b_3.5pt.gif) numărul minim de operaţii necesare pentru a rezolva subarborele nodului
numărul minim de operaţii necesare pentru a rezolva subarborele nodului 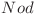 dacă acesta cade spre unul dintre fii şi este doborât de alt fiu
dacă acesta cade spre unul dintre fii şi este doborât de alt fiu
![DP[Nod][2] = DP[Nod][2] =](http://www.infoarena.ro/static/images/latex/029956abf468e2b354621b1ced42d6c4_3.5pt.gif) numărul minim de operaţii necesare pentru a rezolva subarborele nodului
numărul minim de operaţii necesare pentru a rezolva subarborele nodului 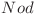 dacă acesta cade spre radacină.
dacă acesta cade spre radacină.
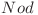 poate să nu fie atins de niciun alt copac.
poate să nu fie atins de niciun alt copac.
![BEST[Nod] = min(DP[Nod][0], \hspace{0.1cm} DP[Nod][1], \hspace{0.1cm} DP[Nod][2]) BEST[Nod] = min(DP[Nod][0], \hspace{0.1cm} DP[Nod][1], \hspace{0.1cm} DP[Nod][2])](http://www.infoarena.ro/static/images/latex/71929015a2e19ac9b5a6299febf4c9a6_3.5pt.gif)
Rădăcina poate să fie orice nod cu grad mai mic sau egal cu 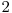 .
.
Să presupunem că ne aflăm în nodul 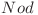 cu fii
cu fii 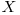 şi
şi 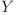 de care se leagă prin muchiile de lungime
de care se leagă prin muchiile de lungime 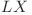 respectiv
respectiv 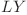 .
.
Iniţializăm ![DP[Nod][0], \hspace{0.1cm} DP[Nod][1], \hspace{0.1cm} DP[Nod][2] DP[Nod][0], \hspace{0.1cm} DP[Nod][1], \hspace{0.1cm} DP[Nod][2]](http://www.infoarena.ro/static/images/latex/1f40e6e578b789d0ca82608d02e35f11_3.5pt.gif) cu
cu ![1 + BEST[X] + BEST[Y] 1 + BEST[X] + BEST[Y]](http://www.infoarena.ro/static/images/latex/a7d4cd8c2bd7d047460c060a8f1b108c_3.5pt.gif) caz în care tai copacul curent fără să afecteze/ să fie afectat de subarborii lui
caz în care tai copacul curent fără să afecteze/ să fie afectat de subarborii lui 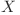 şi
şi 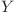 .
.
Dacă 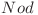 poate să doboare copacul
poate să doboare copacul 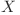 atunci updatez
atunci updatez ![DP[Nod][0] : DP[Nod][0] = min(DP[Nod][0], \hspace{0.1cm} DP[X][0] + BEST[Y]) DP[Nod][0] : DP[Nod][0] = min(DP[Nod][0], \hspace{0.1cm} DP[X][0] + BEST[Y])](http://www.infoarena.ro/static/images/latex/540286fe626173f1427db08cd58d29ba_3.5pt.gif) . Analog pentru
. Analog pentru 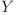 .
.
Dacă 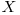 poate să doboare copacul curent atunci updatez
poate să doboare copacul curent atunci updatez ![DP[Nod][2] : DP[Nod][2] = min(DP[Nod][2], \hspace{0.1cm} DP[X][2] + BEST[Y]) DP[Nod][2] : DP[Nod][2] = min(DP[Nod][2], \hspace{0.1cm} DP[X][2] + BEST[Y])](http://www.infoarena.ro/static/images/latex/9599ca070baa3cc4c6259d71271c3f0e_3.5pt.gif) . Analog pentru
. Analog pentru 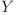 .
.
Dacă 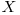 poate sa doboare copacul curent şi
poate sa doboare copacul curent şi 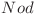 poate să doboare copacul
poate să doboare copacul 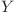 atunci updatez
atunci updatez ![DP[Nod][1] : DP[Nod][1] = min(DP[Nod][1], \hspace{0.1cm} DP[X][2] + DP[Y][0] - 1) DP[Nod][1] : DP[Nod][1] = min(DP[Nod][1], \hspace{0.1cm} DP[X][2] + DP[Y][0] - 1)](http://www.infoarena.ro/static/images/latex/14c5f06a8498877851ca27db8c067439_3.5pt.gif) . Deoarece unesc două lanţuri numarul de operaţii necesare se micşorează cu 1. Analog pentru cazul
. Deoarece unesc două lanţuri numarul de operaţii necesare se micşorează cu 1. Analog pentru cazul 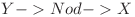 .
.
Subtaskul 5
Soluţia se bazeaza pe acelaşi 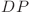 ca la subtaskul 4.
ca la subtaskul 4.
Pentru fiecare nod o să avem nevoie de o variabilă în care reţinem ![\sum_{fiu \in Nod} BEST[fiu] \sum_{fiu \in Nod} BEST[fiu]](http://www.infoarena.ro/static/images/latex/948753fbaa266004fa4bba50c84b2cce_5.36115pt.gif) .
.
![DP[Nod][0] DP[Nod][0]](http://www.infoarena.ro/static/images/latex/735d52f1412899b3f4b0152bd99fb378_3.5pt.gif) şi
şi ![DP[Nod][2] DP[Nod][2]](http://www.infoarena.ro/static/images/latex/ee408f2738250e477cd993f80338a231_3.5pt.gif) se calculează similar.
se calculează similar.
Pentru a calcula ![DP[Nod][1] DP[Nod][1]](http://www.infoarena.ro/static/images/latex/b8aabc3ddcaf8bf795655c9c5c500d79_3.5pt.gif) încercăm să cuplăm nodul curent cu fiecare fiu
încercăm să cuplăm nodul curent cu fiecare fiu 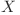 pe rând considerând că
pe rând considerând că 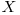 este doborât de copacul curent.
este doborât de copacul curent.
Avem însă nevoie să ştim ce fiu e optim să considerăm că doboară copacul 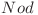 .
.
Să presupunem că exista doi fii 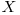 şi
şi 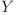 care pot să cadă spre nodul actual. Considerăm că
care pot să cadă spre nodul actual. Considerăm că 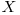 este mai bun ca
este mai bun ca 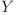 dacă
dacă ![DP[X][2] - BEST[X] < DP[Y][2] - BEST[Y]
DP[X][2] - BEST[X] < DP[Y][2] - BEST[Y]](http://www.infoarena.ro/static/images/latex/8905f184a3b156b991775497ef4c32c9_3.5pt.gif) . Astfel avem nevoie doar de primele două cele mai bune noduri care pot fi determinate printr-o singură parcurgere a fiilor nodului actual.
. Astfel avem nevoie doar de primele două cele mai bune noduri care pot fi determinate printr-o singură parcurgere a fiilor nodului actual.
