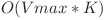Solutia problemei Nave Interdimensionale
Pentru primele 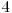 subtaskuri vezi soluţia problemei naveplanare
subtaskuri vezi soluţia problemei naveplanare
Pentru 100 de puncte vom folosi un greedy în care mutăm navele pe rând pentru a obţine o linie/coloană (liniile şi coloanele sunt de fapt independente) nouă pe care se află cel puţin o navă.
Fie![cnt[k] cnt[k]](http://www.infoarena.ro/static/images/latex/f84840677fc10b5be96e420f16d773aa_3.5pt.gif) pentru
pentru 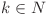 numărul de nave care trec dinspre poziţia
numărul de nave care trec dinspre poziţia  spre poziţia
spre poziţia 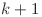 . Dacă
. Dacă ![cnt[k] cnt[k]](http://www.infoarena.ro/static/images/latex/8a5561b8a8205190bf6eb64d9b235871_3.5pt.gif) este negativ, el va reprezenta numărul de nave care trec dinspre poziţia
este negativ, el va reprezenta numărul de nave care trec dinspre poziţia 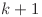 spre poziţia
spre poziţia 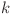 înmulţit cu
înmulţit cu 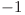 .
.
Observăm acum că costul aferent mişcării unei nave din 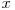 în
în  cu
cu 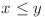 va fi numărul de valori
va fi numărul de valori 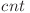 mai mari sau egale cu
mai mari sau egale cu 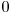 minus numărul de valori
minus numărul de valori 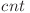 strict mai mici decât
strict mai mici decât 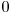 în intervalul
în intervalul ![[x,y-1] [x,y-1]](http://www.infoarena.ro/static/images/latex/7b736b7d3134b0a95e036be557879282_3.5pt.gif) .
.
De ce? Pentru că dacă ![cnt[k] cnt[k]](http://www.infoarena.ro/static/images/latex/8a5561b8a8205190bf6eb64d9b235871_3.5pt.gif) este mai mare sau egal decât
este mai mare sau egal decât 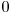 , înseamnă că trebuie să consumăm o secundă pentru a mişca nava între
, înseamnă că trebuie să consumăm o secundă pentru a mişca nava între 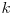 şi
şi 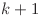 . Dacă
. Dacă ![cnt[k] cnt[k]](http://www.infoarena.ro/static/images/latex/8a5561b8a8205190bf6eb64d9b235871_3.5pt.gif) este mai mic decât
este mai mic decât 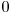 , am putea economisi o secundă: în loc să mişcăm nava asta spre dreapta, vom opri una dintre navele care se mişcă dinspre
, am putea economisi o secundă: în loc să mişcăm nava asta spre dreapta, vom opri una dintre navele care se mişcă dinspre 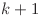 spre
spre 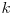 şi vom obţine acelaşi rezultat.
şi vom obţine acelaşi rezultat.
Există mai multe metode în 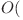 Valoarea Maximă pe care o poate lua o coordonată
Valoarea Maximă pe care o poate lua o coordonată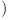 de a găsi mişcarea cea mai ieftină. Trebuie apoi să updatăm valorile din
de a găsi mişcarea cea mai ieftină. Trebuie apoi să updatăm valorile din 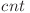 şi să reluăm algoritmul până când numărul de linii care conţin cel puţin o navă este cel dorit.
şi să reluăm algoritmul până când numărul de linii care conţin cel puţin o navă este cel dorit.
Complexitatea finală este