Soluţii Urmasii lui Moisil 2015
Bignumber
Autor: stud. Cosmin Tututnaru, Universitatea „Babeş-Bolyai”, Cluj-Napoca
Descrierea soluţiei (Cosmin Tutunaru)
Soluţie – 50 p
Încercăm să aducem pe prima poziţie cea mai mare cifră care nu se află la o distanţă mai mare decât X (număul de mutări permise). Evident că, dacă cifra apare pe mai multe poziţii, o vom alege pe cea mai din stânga. Aducem această cifră pas cu pas pe prima pozitie si actualizăm X-ul. Eliminăm prima poziţie din şir şi repetăm procesul.
Complexitate: O(X)
Soluţie – 100 pct
Fie getCost(pos) o funcţie care returnează costul minim de a duce cele mai mari pos cifre pe primele pos poziţii. Aceasta funcţie poate fi implementată în O(N) cu constanta 10, deoarece la primul pas aducem toate cifrele de 9 pe prima poziţie, la pas-ul următor toate cifrele de 8, … şi tot aşa, până când sunt aduse cele mai mari pos cifre.
Fie v şirul maxim care se poate obţine (şirul iniţial sortat descrescător).
Având funcţia de mai sus implementată, putem căuta binar primele elemente din v care se vor afla şi in rezultat (fără a fi necesare mai mult de X swap-uri). După ce se află numărul de elemente care coincid, numărul de mutari care ne mai pot rămâne este cel mult N şi putem aplica în continuare algoritmul de la soluţia de 50 de puncte pentru restul cifrelor rămase.
Complexitate: O(N*LogN)
Rox
Autor: stud. Liana Ştefania Ţucăr
Descrierea soluţiei (stud. Marta Diana Filimon)
Solutie – 100 p
Pentru a reţine tipul florilor care sunt plantate în celula de pe linia L şi coloana C vom utiliza un tip de date care este reprezentat pe 32 de biţi şi vom utiliza cei mai nesemnificativi (aceştia fiind ultimii) 26 de biţi, astfel: cel de al k-lea bit este 1 dacă floarea care are numele celei de a (k+1)-a literă a alfabetului englez apare pe linia L şi coloana C, unde 0 <= k <= 25.
Pentru o parcelă de coordonate L1, C1, L2, C2 pe care se plantează o floare de tipul T se procedează astfel: vom aplica operaţia xor cu valoarea 1 deplasată la stânga cu k biţi, unde k reprezintă numărul de ordine al literei în alfabet mărit cu 1, în celulele de coordonate (L1, C1), (L2, C2+1), (L2+1, C1), (L2+1, C2+1).
Vom face suma xor pentru elementele aflate în submatricea care are colţurile în celulele (1, 1) şi (L, C) oricare ar fi L şi C cu 1 <= L <= N; 1 <= C <= M. Apoi, pentru a răspunde unei întrebări din cele Q întrebări date, vom determina numărul de biţi de 1 al reprezentării binare a valorii de pe linia şi coloana specificată.
Observăm că nu poate fi reţinută matricea sumelor xor, însă acest lucru nu este necesar deoarece pentru a determina valoarea oricărei celule de pe linia i avem nevoie cel mult de linia i-1. Într-o astfel de abordare, soluţia problemei se modifică asftel:
- Se reţin de la început atât plantările cât şi întrebările.
- Pentru fiecare plantare vom reţine separat prima linie şi ultima linie pe care apare, deoarece în rest aceasta nu modifică suma xor a valorilor din celule; se observă că astfel se dublează numărul de plantări.
- Se sortează crescător dupa linie plantările, iar întrebările se sortează crescător după linie şi, în caz de egalitate, după coloană.
- Pe măsură ce determinăm răspunsurile întrebărilor, le reţinem; la final le sortăm după ordinea apariţiei în fişierul de intrare.
Observăm că pentru a calcula sumele xor de pe o linie nu este necesar să reţinem sumele xor de pe linia precedentă, noile plantări aplicându-se peste cele anterioare. Pentru a răspunde la întrebările de pe o linie i, facem suma xor a valorilor de pe linia respectivă doar în cazul în care avem o întrebare.
Inception
Autor: stud. Ştefan Negruş, Facultatea de Informatică Iaşi, Universitatea Al. I. Cuza
Descrierea soluţiei (stud. Ştefan Negruş)
Iniţial avem nevoie de câteva observaţii ce ne vor ajuta în descrierea soluţiilor următoare: din faptul că nu se folosesc poziţiile [i][j] în care sunt visate elementele iar un element nu poate fi visat de mai multe ori, putem deduce că nu avem nevoie să reţinem matricele sub forma de tablou bidimensional si nici să reţinem elementele care s-au modificat. Astfel, orice matrice este reprezentată doar prin id-ul şi coeficientul sau (informaţii suplimentare în soluţi).
Astfel, problema se reduce la forma următoare: fiecare matrice este echivalentul unui element într-o listă simplu înlănţuită. Unele liste se pot intersecta cu alte liste.
Exemplul din enunt:
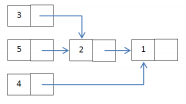
Totodată trebuie să ţinem cont de operaţiile de update. O operaţie de adăugare a unei valori la coeficienţii a nr matrici este echivalentă acum cu adăugarea unei valori la fiecare element dintr-o secvenţă, de lungime nr, de elemente inlănţuite.
Listele pot fi reţinute static: next[i] = indicele elementului ce urmează dupa elementul cu indice i
Sau pot fi reţinute dinamic: next[i] = pointer la primul element din secvenţa de elemente care începe la elementul cu indice i şi se termina la elementul cu indice 1.
Solutie – 20p – Complexitate(N)
Observăm că daca am avea o singură listă care nu este intersectată de o altă listă, elementele sunt numerotate crescător de la 1 şi putem face update-ul pe secvenţa în O(1): coeficient[id] += val, coeficient[id – nr] –= val. Iar la sfârşit calculăm valoarea finală pentru fiecare matrice.
Solutie – 40p – Complexitate (N2)
La o operaţie de adaugare de element se adaugă/creează elementul şi se face legatura necesară. Operaţia de tip update pe secventaţă este echivalentă cu parcurgerea secvenţei ce începe cu elementul id şi adaugarea valorii val la nr elemente. Coeficientul fiecărui element, obţinut dupa efectuarea tuturor operaţiilor, este final.
Solutie – 60p – Complexitate(N2)
Putem combina foarte usor soluiile precedente pentru a prinde mai multe cazuri. Trebuie să ştim dacă avem cel puţin o matrice în care există mai mult de 1 element visat. Iniţial folosim strategia de la soluţia de 20p descrisă mai sus şi memorăm într-un vector pentru fiecare element câte elemente sunt visate în matricea respectivă. Dacă în urma unui eveniment de tip 1 o matrice conţine cel puţin 2 elemente putem calcula valorile parţiale ale coeficienţilor pentru toate elementele până în acel moment şi în continuare aplicăm strategia descrisă la soluţia ce obţine 40p.
Solutie – 80p – Complexitate(N*sqrtN)
Atunci când avem mai multe liste trebuie să accesam eficient elementul la distanţa nr fata de id. Putem face asta dacă din fiecare element reţinem elementul la distanţa sqrt(N) faţă de elementul curent. Atunci când trebuie să găsim elementul la distanţa nr facem nr/sqrt(N) paşi “mari” de la un element la altul, înspre elementul 1, elemente care sunt la distanţa sqrt(N) între ele. La sfârşit mai facem maxim sqrt(N)–1 paşi “mici” de distanţa 1 până la elementul căutat. Numărul total de paşi va fi de ordinul O(sqrtN).
Solutie – 100p – Complexitate(N*logN)
Putem îmbunătăţi soluţia de mai sus memorând pentru fiecare element al 2^k (k din [1,20]) element înspre elementul cu indicele 1. Astfel numărul de paşi va fi de ordinul numărului de biţi cu valoarea 1 din reprezentarea binară a numărului nr care este de ordinul O(logN).
De menţionat că pentru ultimele 2 soluţii calcularea valorilor finale ale coeficienţilor se face la sfârşit. Trebuie să procesăm mereu elementele de la capetele listelor spre elementul 1. Echivalent cu a parcurge matricile începând cu cele care nu au alte matrice formate în interior. Putem face asta cu o coadă în care punem iniţial capetele listelor şi procesăm fiecare element pe rând astfel: adăugam valoarea din elementul curent la următorul element din lista şi dacă acel element a devenit capătul unei liste (nu se află în interiorul niciunei liste) îl adăugăm în coadă. Afişăm răspunsul pentru fiecare id cerut în O(1).
Puncte4
Autor: Vlad Stoian, software development engineer, Amazon România
Descrierea soluţiei (Vlad Stoian)
Soluţie – 100 p – Complexitate O(N2*K)
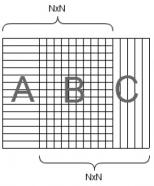
Elementele din imaginea alăturată reprezintă 2 pătrate NxN vecine. A este numărul de puncte de pe prima coloană, B numărul de puncte de pe următoarele N-1 coloane şi C de pe ultima coloana. Din enunţ ştim că A + B = P, respectiv B + C = P. De aici deducem că A = C. Asta înseamnă că dacă alegem ca pe prima coloană să punem un număr de puncte, la fel vom alege şi pentru toate coloanele pentru care i % n == 1. Generalizând, fiecare coloană va avea acelaşi număr de puncte ca i - n si i + n.
Fie nrci numărul de puncte de pe coloana i. Împărţim coloanele pe N clase de echivalenţă pe baza operaţiei i % n. Fie clsi numărul de coloane din clasa de echivalenţă i.
Observăm că, in funcţie de M, o coloană va putea fi găsită de M / N sau M / N + 1 ori aşadar clsi va putea lua doar două valori. Sunt Comb(n, k)clsi posibilităţi de a aranja P puncte in fiecare dintre cele clsi coloane, deci toate combinările la puterile M / N si M / N + 1 pot fi precalculate. Deoarece M / N poate fi un număr destul de mare, vom folosi un algoritm de ridicare rapidă la putere.
Pornind de la aceste descoperiri, ajungem la 2 idei de rezolvare.
1. Partiţionarea sumei P (backtracking)
Încercăm să partiţionăm P în p1, p2, .. pn unde Suma(pi) = P.
2. Programare dinamică
Fie dp[i][j] numărul de posibilităţi de a umple toate coloanele din clasele 1 până la i, astfel încât Suma(nrck) = j;
De aici rezultă că:
dp[i][j+k] = suma pentru K = 0 <- P-j din dp[i-1][k] * Comb(n, k)clsi
Se observa si ca, pentru x > i * i / 2, dp[i][x] == dp[i][i * i - x].
Implementarea recursivă primeşte 80 de puncte, iar cea iterativă 100 de puncte.
Naveplanare
Autor: stud. Cosmin Tututnaru, Universitatea „Babeş-Bolyai”, Cluj-Napoca
Descrierea soluţiei (Cosmin Tutunaru)
Soluţie – 100 pct
Putem descompune problema pe OX şi OY, având în vedere că mişcările sunt independente. În acest fel putem sorta separat toate valorile X şi toate valorile Y.
În continuare avem de rezolvat următoarea problema: având un vector V sortat, să se determine numărul minim de operaţii necesare astfel încât să avem minim K valori distincte în el. O operaţie înseamna creşterea/scăderea cu 1 a oricărui element din vector.
Vom folosi următoarea dinamică:
DP(i, j, k) = numărul minim de operaţii necesare pentru a avea exact j poziţii distincte formate din primele i numere, iar numarul de pe poziţia i are orice valoare din intervalul [-inf, k]
DP(i, j, k) = min(
● DP(i-1, j-1, k-1) + abs(V[i] - k), “Vom creste numarul de elemente distincte cu 1, deci va trebui sa ducem elementul v[i] la valoarea k”
● min(DP(i-1, j, k), DP(i, j, k-1))
);
Solutia va fi minimul dintre toate DP (N, K..N, 0..max(v) + size(v)))
Răspunsul la problema va fi suma acestor doua minime (pentru X şi pentru Y).
Complexitate: O(N*N*K)
O altă soluţie care obtine 100 de puncte se poate implementa cu flux.
Geometrie
Autor: drd. Paul Diac, Facultatea de Informatică Iaşi, Universitatea Alexandru Ioan Cuza
Soluţie – 100p – Complexitate O(MlogN)
Se construieşte pas cu pas infăşuratoarea convexă a punctelor din stânga oricarui punct din mulţimea A. La fiecare etapă, avem înfăşuratoarea convexă a punctelor din stânga unei anumite limite x şi se adauga următorul punct din mulimea A, care este cel mai din stânga punct de dupa aceasta limită (din dreapta limitei).
Se răspunde dupa acest pas la toate întrebarile care au coordonata x între cel mai din dreapta punct din mulţimea punctelor procesate din A şi mulţimea punctelor neprocesate înca.
Alte detalii: avem nevoie astfel de două tipuri de operaţii. Pe prima o vom numi ‘update’, reprezintă adăugarea la înfăşuratoare a unui punct din (strict) dreapta înfaşurătorii. Operaţia ‘query’ cere determinarea ariei înfăşurătorii convexe a unei înfăşurători reunite cu un ‘punct de query’, dar acest punct nu va rămâne pe înfăşuratoare decât pentru acest query. Similar cu update, acest punct este în (strict) dreapta infăşurătorii.
Atat pentru update cât şi pentru query trebuie determinate ‘tangentele’ unui punct la un poligon convex deja calculat. Dacă punctele de pe înfăşurătoarea convexă sunt reţinute în două stive (pentru partea superioară şi partea inferioară); in aceste stive se poate itera liniar pentru a găsi punctul tangent la poligon, unde sensul / aria triunghiului cu semn işi schimbă semnul (triunghiul format din ‘punctul de query’ şi două puncte consecutive de pe înfăşurătoare). Deoarece semnul se schimbă de la o poziţie şi se menţine mai departe, se poate căuta binar poziţia, pentru soluţia optimă. Observaţie: pentru query e necesar să căutam binar punctele ‘tangente’, însă pentru update se poate căuta liniar, deoarece punctele iterate vor fi scoase de pe înfăşurătoare o singura dată, deci, aceste operaţii se vor amortiza. Algoritmul pentru partea de update este un algoritm clasic numit Andrew’s algorithm. Punctele sunt reţinute în stive similar ca idee cu algoritmul Graham scan: un update poate elimina de pe înfăşurătoare un număr oarecare de puncte, dar ele vor fi eliminate o singură dată.
Pentru a calcula în timp constant ariile, trebuie precalculată aria “din partea stânga” pentru fiecare punct de pe înfăşurătoarea convexă, de exemplu: aria proiecţiei pe OX a segmentelor de pe înfăşurătoare de la cel mai din stânga punct până la punctul curent, atât pentru punctele de pe stiva superioară cât şi pentru cea inferioară. Evident, când se inserează un punct, aria este suma dintre aria precalculată pentru punctul cu care se învecinează în stânga şi aria trapezului dreptunghic care se află sub acest segment nou. Răspunsul pentru un query este diferenţa ariilor precalculate pentru stiva superioară şi cea inferioară.
Solutie – 80p – Complexitate O(M * N)
Se implementează algorimul descris mai sus, mai puţin căutarea binară (se caută liniar).
Solutie – 60p – Complexitate O(M * NlogN)
Se reconstruieşte complet la fiecare pas (punct Ai de la stânga la dreapta) înfăşuratoarea convexă a punctelor din stânga. Algoritmul de determinare a înfăşurătorii convexe este unul de complexitate O(N log N), de exemplu Graham scan. Aria se calculeaza de fiecare dată în O(N), cu algoritmul clasic.
Solutie – 40p – Complexitate O(M * N2)
Se reconstruieşte la fiecare pas înfăşurătoarea convexă în O(N2), de exemplu folosind algoritmul Javis March (împachetarea pachetului). Aria se calculează de fiecare data în O(N).
Solutie – 20p – pentru N ≤ 3
Poligoanele pentru care trebuie calculată înfăşurătoarea convexă sunt fie triunghiuri, fie patrulatere. Pentru triunghiuri, se poate aplica direct formula pentru aria unui triunghi şi se obţin 10 din cele 20 puncte doar cu atât. Pentru patrulatere, înfăşuratoarea convexă poate fi un triunghi sau un patrulater şi trebuie tratate corect ambele cazuri.
