Solutia problemei Cuantictiori
 Se asigură că se poate demonstra că numărul de progresii geometrice de lungime
Se asigură că se poate demonstra că numărul de progresii geometrice de lungime  care au prima valoare egală cu
care au prima valoare egală cu 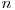 este egal cu cel mai mare număr natural
este egal cu cel mai mare număr natural 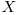 cu proprietatea că
cu proprietatea că 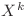 este divizor al lui
este divizor al lui  .
.
Pentru demonstraţie vedeţi soluţia problemei nambartiori.
Fie  cel mai mare divizor comun al exponenţilor din descompunerea în factori primi a lui
cel mai mare divizor comun al exponenţilor din descompunerea în factori primi a lui  .
.
Vom demonstra mai întai că dacă 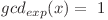 , atunci
, atunci 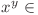 cu
cu 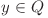 numai dacă
numai dacă 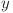 se află de asemenea şi în
se află de asemenea şi în 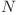 . (Lema 1)
. (Lema 1)
Fie 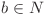 astfel încât
astfel încât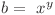 şi
şi 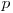 şi
şi 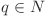 cu proprietatea că
cu proprietatea că 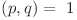 , astfel încât
, astfel încât 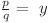 .
.
Atunci 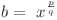 şi deci
şi deci 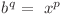 .
.
Dacă 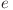 şi
şi 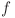 sunt exponenţii factorului prim
sunt exponenţii factorului prim 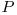 din descompunerea în factori primi a numerelor
din descompunerea în factori primi a numerelor 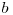 şi respectiv
şi respectiv  , reiese că:
, reiese că: 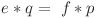 .
.
Ştim că 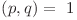 , deci
, deci 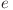 va trebui să fie divizibil cu
va trebui să fie divizibil cu 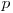 şi
şi 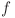 va trebui să fie divizibil cu
va trebui să fie divizibil cu 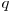 .
.
Ştiind că acest lucru se aplică pentru orice număr prim 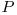 , putem deci spune că toţi exponenţii din descompunerea în factori primi a numărului
, putem deci spune că toţi exponenţii din descompunerea în factori primi a numărului  vor fi divizibili cu
vor fi divizibili cu 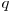 .
.
Deci cel mai mare divizor comun al exponenţilor din descompunerea în factori primi a numărului  va fi divizibil cu
va fi divizibil cu 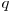 .
.
Din moment ce 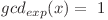 , va trebui ca şi
, va trebui ca şi 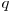 să fie egal cu
să fie egal cu  .
.
Atunci  , ceea ce trebuia demonstrat.
, ceea ce trebuia demonstrat.
Dacă 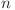 este primul termen,
este primul termen, 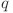 este raţia şi progresia cuantică are lungimea
este raţia şi progresia cuantică are lungimea 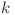 , condiţia de existenţă este următoarea:
, condiţia de existenţă este următoarea:
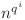 este natural pentru oricare
este natural pentru oricare 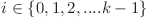 .
.
Fie 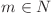 astfel încât
astfel încât 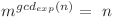 . Intuitiv,
. Intuitiv, 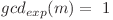 . Înlocuind mai sus, obţinem:
. Înlocuind mai sus, obţinem:
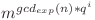 este natural pentru oricare
este natural pentru oricare 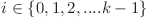 .
.
Folosing Lema 1, obţinem că:
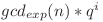 este natural pentru oricare
este natural pentru oricare 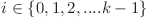 .
.
Observăm astfel că am ajuns la problema nambartiori, doar că aplicata valorii 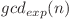 .
.
Subtaskul 2
Putem să trecem prin fiecare numar, să-i calculam  -ul si să-i aplicam functia din nambartiori ca apoi să-l adaugam la rezultat.
-ul si să-i aplicam functia din nambartiori ca apoi să-l adaugam la rezultat.
Subtaskul 3
Observăm că un numar 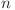 ne interesează doar dacă
ne interesează doar dacă 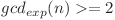 . Asta înseamnă că în loc să trecem prin toate numerele pana la
. Asta înseamnă că în loc să trecem prin toate numerele pana la 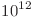 , putem pur şi simplu să mergem prin bazele acestor numere până în
, putem pur şi simplu să mergem prin bazele acestor numere până în 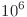 . Prin baze ne referim la numerele
. Prin baze ne referim la numerele 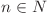 cu proprietatea că
cu proprietatea că 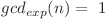 .
.
