Soluţia problemei Nambartiori
Notăm cu 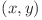 cel mai mic divizor comun dintre
cel mai mic divizor comun dintre 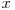 şi
şi 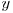 .
. 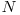 şi
şi 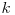 au semnificaţia din enunţ.
au semnificaţia din enunţ.
Cazul cu 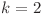 o sa îl tratăm separat. Se observă că orice două numere naturale
o sa îl tratăm separat. Se observă că orice două numere naturale 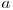 şi
şi 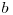 cu
cu 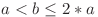 formează o progresie geometrică validă, deoarece
formează o progresie geometrică validă, deoarece 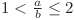 . Deci numărul de progresii geometrice care încep cu un număr
. Deci numărul de progresii geometrice care încep cu un număr 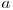 este chiar
este chiar 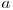 .
.
Fie 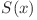 numărul de progresii geometrice de lungime
numărul de progresii geometrice de lungime 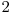 care încep cu un număr mai mic sau egal decât
care încep cu un număr mai mic sau egal decât 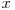 şi au raţia între
şi au raţia între 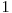 şi
şi 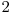 . Conform observaţiei de mai sus
. Conform observaţiei de mai sus 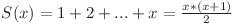 . Putem afla prima poziţie din progresia geometrică cu o căutare binară în
. Putem afla prima poziţie din progresia geometrică cu o căutare binară în 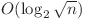 sau cu o parcurgere simplă în
sau cu o parcurgere simplă în 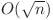 . Mai departe este foarte simplu să aflăm care este progresia cerută.
. Mai departe este foarte simplu să aflăm care este progresia cerută.
Fie 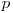 primul termen al unei progresii. Putem scrie raţia unei progresii ca
primul termen al unei progresii. Putem scrie raţia unei progresii ca 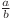 , unde
, unde 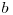 şi
şi 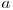 sunt numere naturale prime între ele astfel încât
sunt numere naturale prime între ele astfel încât 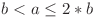 .
.
Avem 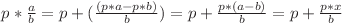 . Cum
. Cum 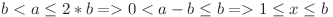
În loc de a afla numărul de fracţii 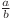 putem afla numărul de fracţii de forma
putem afla numărul de fracţii de forma 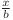 , cu
, cu 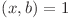 si
si 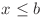 , pentru că sunt echivalente conform demonstraţiei de mai sus.
, pentru că sunt echivalente conform demonstraţiei de mai sus.
Dacă vrem ca progresia să aibă 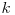 termeni, atunci ne interesează fracţiile pentru care numărul
termeni, atunci ne interesează fracţiile pentru care numărul 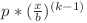 este număr natural. Cum
este număr natural. Cum 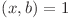 , proprietatea anterioară este echivalentă cu
, proprietatea anterioară este echivalentă cu 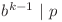 .
.
Rămâne să numărăm câte fracţii există. Pentru un 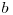 valid,
valid, 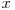 poate lua valori doar numere mai mici sau egale cu
poate lua valori doar numere mai mici sau egale cu 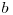 astfel încât
astfel încât 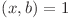 , deci numarul de fracţii este
, deci numarul de fracţii este 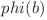 (Indicatorul lui Euler).
(Indicatorul lui Euler).
Fie 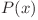 numărul de progresii geometrice de lungime
numărul de progresii geometrice de lungime 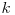 care încep cu
care încep cu 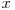 şi au raţia mai mare strict decât
şi au raţia mai mare strict decât 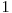 şi mai mică sau egală cu
şi mai mică sau egală cu 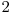 . Conform observaţiei de mai sus
. Conform observaţiei de mai sus 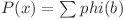 , unde
, unde 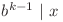 .
.
Fie 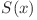 numărul de progresii geometrice de lungime
numărul de progresii geometrice de lungime 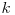 care încep cu un număr mai mic sau egal decât
care încep cu un număr mai mic sau egal decât 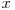 şi au raţia între
şi au raţia între 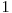 şi
şi 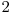 . Aşadar
. Aşadar 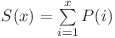 . Dacă extindem suma obţinem
. Dacă extindem suma obţinem 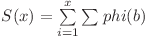 , unde
, unde 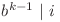 . Putem calcula suma rapid dacă aflăm pentru fiecare
. Putem calcula suma rapid dacă aflăm pentru fiecare 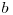 de câte ori apare
de câte ori apare 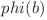 în sumă.
în sumă. 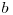 poate lua valori până la
poate lua valori până la ![\sqrt[k-1]x \sqrt[k-1]x](http://www.infoarena.ro/static/images/latex/535c3a8cd9f211a094688120c0e29273_3.39725pt.gif) , iar
, iar 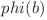 apare de
apare de 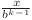 ori în sumă. Deci putem calcula
ori în sumă. Deci putem calcula 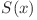 în
în ![O(\sqrt[k-1]x) O(\sqrt[k-1]x)](http://www.infoarena.ro/static/images/latex/32f4b99e7788b1b10a5145901621dbc1_3.5pt.gif) . Căutăm binar prima valoare din progresie. Fie aceasta
. Căutăm binar prima valoare din progresie. Fie aceasta 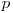 . Fie
. Fie 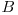 cel mai mare numar astfel încât
cel mai mare numar astfel încât 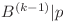 . Observăm că
. Observăm că 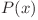 poate fi scris ca
poate fi scris ca 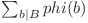 , dar această sumă este egală cu
, dar această sumă este egală cu 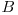 deoarece
deoarece 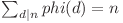 . Fie fracţiile
. Fie fracţiile 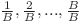 . Numărul acestora este
. Numărul acestora este 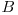 , ele fiind distincte două câte două, iar pentru că
, ele fiind distincte două câte două, iar pentru că 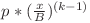 este natural, înseamnă că progresiile geometrice valide care încep cu p sunt doar cele care au raţiile egale cu
este natural, înseamnă că progresiile geometrice valide care încep cu p sunt doar cele care au raţiile egale cu 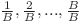 . Pe noi ne interesează
. Pe noi ne interesează 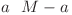 progresie geometrică care începe cu
progresie geometrică care începe cu 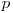 , unde
, unde 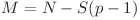 . Conform observaţiilor anterioare aceasta este
. Conform observaţiilor anterioare aceasta este 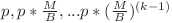 . Complexitatea finală pentru a afla
. Complexitatea finală pentru a afla 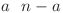 progresie geometrică de lungime
progresie geometrică de lungime 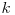 este
este ![O(\sqrt[k-1]n * \log_{2}n) O(\sqrt[k-1]n * \log_{2}n)](http://www.infoarena.ro/static/images/latex/31428f337e8b5a255e517e6ba8bf9244_3.5pt.gif) .
.
