Soluţii ONIS 2014, Runda 4
- Lista de probleme
- Football
- Curs Valutar
- Bani
- Cercuri5
- Cuvant
- Speculum
- Dans
- Subsiruri3
- Joc17
- Arhipelag
Football
În alte cuvinte, problema ne cere să determinăm numărul de moduri distincte în care un număr S poate fi scris ca sumă de 1, 2, 3, 6.
Datorita limitelor reduse ale inputului putem rezolva problema cu o abordare de tip backtracking in care generam toate solutiile posibile:
int P[] = {1, 2, 3, 6};
void back(int c, int S) {
if (c == S) {
++nr;
return;
}
for (int i=0; i<4; ++i)
if (c+P[i]<=S) back(c+P[i], S);
}O alta varianta de a rezolva problema este folosind programare dinamica. Vom construi un vector auxiliar cu următoarea semnificaţie:
- d[i] = numărul de moduri distincte în care poţi scrie i ca sumă de 1, 2, 3 şi 6.
Pentru a calcula d[i], ne vom folosi de stările precedente deja calculate astfel:
- d[i] = d[i - 1] + d[i - 2] + d[i - 3] + d[i - 6].
Răspunsul pentru fiecare test se va găsi în d[S]. Acest algoritm are complexitate lineara si ar merge bine si daca limitele problemei ar fi mult mai mari.
Curs Valutar
Observatii:
1. Nu are rost sa detinem la un moment dat monede de mai multe tipuri.
Daca am imparti suma S = S1 + S2 si am investi separat S1 si S2, dupa un timp am obtine sumele T1 = S1 * k, respectiv T2 = S2 * q. Presupunem (fara a pierde din generalitate) k >= q, de unde rezulta ca maximizam profitul in cazul in care S1 = S, iar S2 = 0.
2. Este suficient sa efectuam operatiile de vanzare/cumparare doar in zile consecutive.
Daca avem o anumita moneda in ziua A la cotatia Ca, prin vanzarea ei in ziua B >= A+2 la cotatia Cb obtinem o multiplicare a sumei cu Cb/Ca. Fie ziua C in intervalul (A, B) avand cotatia Cc. Daca am efectua tranzactiile pe intervalurile [A, C], respectiv [C, B] am obtine o multiplicare a sumei cu Cc/Ca * Cb/Cc = Cb/Ca, adica exact ceea ce am obtinut si in primul caz.
Obtinem astfel un algoritm greedy care incearca sa maximizeze profitul pentru fiecare doua zile consecutive. Complexitatea algoritmului este O(N*Z).
O solutie care nu tine cont de cea de-a doua observatie se poate obtine folosind programare dinamica: P[i][j] = profitul maxim pe intervalul [i, j]. O astfel de abordare duce la o complexitate O(N*Z2) si trebuie mult optimizata pentru a putea obtine punctajul maxim.
Atentie la ordinea for-urilor! Suntem tentati sa procesam matricea "pe zile", coloana cu coloana. Este de preferat sa parcurgem matricea pe linii si nu pe coloane pentru a nu face salturi prin memorie.
for (int i=0; i<N; ++i) {
scanf("%lf", &c1);
for (int j=1; j<Z; ++j) {
scanf("%lf", &c2);
r[j] = max(r[j], c2 / c1);
c1 = c2;
}
}
for (int j=1; j<Z; ++j)
S *= r[j];Bani
Sa presupunem ca am avea doi rucsaci, fiecare suportand greutatea maxima G1, respectiv G2, iar G1 + G2 = G. O alta conditie este ca in primul rucsac putem pune doar obiecte nepartitionabile, iar in al doilea putem pune doar obiecte partitionabile. Cele doua probleme care rezulta sunt cunoscute sub numele de "problema rucsacului", cazul discret, respectiv continuu. Primul caz se poate rezolva prin programare dinamica, cel de-al doilea prin greedy. Nu voi intra in detalii algoritmii fiind extrem de cunoscuti.
Revenind la problema, vom incerca toate variantele de a il scrie pe G = G1 + G2 si vom retine varianta cea mai buna. Observam ca pentru a rezolva problema rucsacului (indiferent de caz) pentru greutatea G inevitabil vom trece prin toate starile 0, 1, ..., G-1. Asadar nu este nevoie sa rulam algoritmul pentru fiecare partitionare, pentru ca vom avea deja precalculate toate valorile necesare dintr-o singura rulare.
Cercuri5
Fiind date punctele de intersectie a doua cercuri, precum si razele cercurilor, putem determina cu usurinta cu matematica de clasa a 7-a cele doua centre ale cercurilor.
Cum? Vom forma un triunghi isoscel in care cunoastem lungimea tuturor laturilor. Din teorema lui Pitagora putem determina inaltimea. Cu o constructie suplimentara obtinem doua triunghiuri asemenea, in care egalam rapoartele care determina sinusul/cosinusul, astfel determinand pozitia celui de-al treilea varf al triunghiului (centrul cercului).
Tot ce trebuie sa facem in continuare este sa determinam numarul de centre distincte. Putem face acest lucru in mod optim folosind hashing. O solutie bazata pe sortare si comparare este si ea acceptabila.
O problema importanta de care ne lovim sunt erorile de precizie cauzate de operatiile cu numere reale. Atat varianta cu hashing cat si cea cu sortare pot esua daca nu normalizam corespunzator rezultatele obtinute. Vom efectua comparatiile la nivelul primelor 3 zecimale, convertind numere de forma xxx.abcde (double) in xxxabc (int).
Daca incercam sa aproximam folosind partea intreaga:
x = floor(x * 1000);
x = (int)(x * 1000);
vom constata ca rezultate de genul 1.9999 si 2.0001 conduc la reprezentari total diferite.
O varianta buna ar fi urmatoarea:
x = round(x * 1000);
O alta problema de care concurentii s-au lovit a fost sortarea inainte de normalizare. Ganditi-va ce se intampla pe un caz de genul
(0.9999, 2), (0.9999, 3), (1.0001, 2)
In toate datele de test am generat cercuri cu distanta cel putin o unitate intre centre.
Cuvant
Fie A[i][j] = numarul de cuvinte de lungime j pe care le putem forma cu primele i litere din alfabet. Obtinem urmatoarea recurenta:
A[i][j] = A[i-1][j-k] * Combinari(j, k)
Practic avem de pus litera i pe k pozitii dintre cele j.
Observam ca atat pentru calculul matricii A cat si al combinarilor avem nevoie doar de ultimele doua linii ale matricii. Am fost totusi generos si nu am limitat memoria :) dar implementarea acestui "trick" este un exercitiu bun si este deseori necesara.
Speculum
Ideea este de a reduce suma dreptunghiului initial la o suma de dreptunghiuri cu coordonate mai mici si apoi sa aplicam recursiv acest principiu:
La fiecare pas vom considera cea mai mare axa de simetrie (putere a lui 2) care nu depaseste valoarea x2 sau y2. Dreptunghiul este 'taiat' de doua axe pe OX si OY si se reduce simplu la suma de valori ale maxim altor 4 dreptunghiuri care se incadreaza in patratul stanga-sus (injumatatind astfel coordonatele), pe baza oglindirilor specificate in enunt.
Dreptunghiurile se pot reduce direct prin simetrii sau in cazul cu valorile 1 si 2 interschimbate se poate aplica formula (3 * Aria - Suma_redusa) pentru a calcula aceasta reducere in aceeasi maniera.
Se poate precalcula o matrice de dimensiuni 1024 × 1024 eventual impreuna cu sumele dreptunghiurilor de coordonate (1, 1), (x, y) : stanga-sus pentru a putea raspunde in O(1) pentru orice dreptunghi care are coordonatele <= 1024. De la 109 scadem exponential prin injumatatiri maxim ~ 20 pasi pentru a ajunge la dimensiunea precalculata. O solutie care face 4 apeluri recursive insa nu este suficient de rapida (420 apeluri per query), insa sa pot obtine doar 2 astfel de apeluri.
Folosim de la inceput metoda de calcul a sumei unui dreptunghi (x1, y1), (x2, y2) ca fiid (SS[x2][y2] - SS[x1-1][y2] - SS[x2][y1-1] + SS[x1-1][y1-1]), unde SS[x][y] = suma stanga-sus adica a numerelor din dreptunghiul (1, 1), (x, y), iar apoi vom reduce doar la dreptunghiuri de acest tip.
Un astfel de dreptunghi se poate reduce la maxim 2 alte drepunghiuri similare, analizand atent toate cazurile pentru ognindiri si realizand un singur apel pentru dreptunghiuri care intra indentic de mai multe ori la suma (similar pentru diferente). Alt aspect care trebuie avut in vedere pentru reduceri este faptul ca suma dintre un dreptunghi de anumite coordonate si aceelasi dreptunghi dar care are valorile 1 si 2 interschimbate este egala cu (3 * Aria).
Un ultim pas pentru a reduce la 2 apeluri este precalcularea sumei oricarui dreptunghi (1, 1) (p2, p2) unde p2 e o putere a lui 2, dupa o formula de recurenta usor de intuit ( sum[p2] = 2 * sum[p2/2] + 3 * (p2/2) * (p2/2) = 3 dreptunghiuri de aceeasi suma plus unul cu valorile 1 si 2 interschimbate).
In practica solutia poate face si 3 apeluri la fiecare pas sau se poate renunta la precalcularea 1024 × 1024, ambele variante incadrandu-se in limita de timp.
Dans
Consideram cei N participanti noduri in graf, iar perechile compatibile muchii ale aceluasi graf. Se observa cu usurinta ca o ordine valida de dans reprezinta un ciclu sau un lant eulerian in acest graf. Prin urmare, daca graful admite un ciclu sau un lant eulerian, atunci exista solutie si se afiseaza un ciclu/lant eulerian. Faptul ca nu exista mai multe muchii intre aceleasi doua noduri elimina din start problema unui dansator de a dansa 3 dansuri consecutive.
Mai multe detalii legate de gasirea unui ciclu sau lant eulerian puteti gasi aici.
Subsiruri3
Problema se rezolva prin metoda programarii dinamice. Fie A[i] numarul de subsiruri care se termina cu elementul xi. Avem urmatoarea relatie de recurenta:
A[i] = 1 + 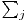 A[j] unde j < i si 0 ≤ xi - xj ≤ K. Solutia naiva are complexitatea O(N2) si nu se incadreaza in limita de timp.
A[j] unde j < i si 0 ≤ xi - xj ≤ K. Solutia naiva are complexitatea O(N2) si nu se incadreaza in limita de timp.
Pentru a optimiza algoritmul putem folosi un arbore indexat binar. Sortam crescator elementele sirului dat mai intai dupa valoare iar in caz de egalitate dupa pozitia in sirul initial (in cazul in care avem xi = xj si i < j atunci vom considera ca xi va fi plasat inaintea lui xj in vectorul sortat). Fie P[i] pozitia elementului xi in vectorul sortat (pozitiile se numeroteaza incepand cu 1). De asemenea fie Q[i] pozitia in vectorul sortat a celui mai mare element xj cu proprietatea ca xi - xj > K (in cazul in care nu exista un astfel de element Q[i] = 0).
Initial vom considera toate valorile A[i] ca fiind egale cu 0. Vom calcula in ordine valorile A[1], A[2], …, A[n] dupa urmatoarea formula A[i] = A[Q[i]+1] + A[Q[i]+2] + … + A[P[i]-1]. Corectitudinea acestei abordari se bazeaza pe faptul ca, in momentul in care calculam valoarea A[i], valorile A[j] cu j > i vor fi egale cu 0. Folosind un arbore indexat binar putem calcula valoarea A[i] in timp O(log N). Complexitatea totala a algoritmului este O(N log N).
Joc17
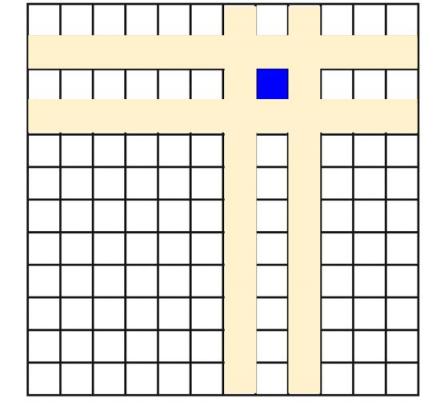
Daca primul jucator coloreaza casuta albastra, cel de-al doilea jucator isi poate adjudeca oricare dintre cele 4 linii galbene precum si suprafata din spatele ei. Si avand in vedere ca joaca optim o va alege pe cea mai mare. Asadar primul jucator va trebui sa inceapa cat mai aproape de centru.
Distingem doua cazuri:
- exista o casuta fix in mijlocul tablei de joc, caz in care primul jucator castiga
- nu exista o astfel de casuta, caz in care ambii jucatori vor colora la fel de multe casute, iar primul jucator nu va mai putea face nicio mutare si va pierde.
Arhipelag
Daca modelam problema sub forma unui graf, atunci fiecare arhipelag va fi o componenta conexa. Determinarea tuturor componentelor conexe impreuna cu dimensiunile lor se poate realiza printr-o parcurgere in adancime sau in latime. Daca dimensiunile datelor de intrare ar fi de ordinul sutelor de mii de noduri ar fi de preferat o parcurgere in latime pentru ca este mai usor de implementat iterativ (in cazul recursivitatii suntem limitati de stack memory). Totusi pentru aceasta problema oricare parcurgere se comporta la fel de bine.
Dimensiunile componentelor sunt apoi sortate si atribuite jucatorilor conform regulilor jocului.
