| Fişierul intrare/ieşire: | ciclueuler.in, ciclueuler.out | Sursă | Arhiva educationala |
| Autor | Arhiva Educationala | Adăugată de | |
| Timp execuţie pe test | 0.4 sec | Limită de memorie | 65536 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Ciclu Eulerian
Fie un multigraf G = (V,E). Un ciclu al lui G se numeste Eulerian daca viziteaza toate muchiile din E exact o singura data. G se numeste Eulerian daca admite un ciclu Eulerian.
Cerinta
Fiind dat un multigraf G = (V,E), determinati daca acesta este Eulerian. In caz afirmativ, gasiti un ciclu Eulerian al sau.
Date de intrare
Fisierul de intrare ciclueuler.in contine pe prima linie numerele N si M, reprezentand numarul nodurilor, respectiv numarul muchiilor din G. Pe urmatoarele M linii se afla cate o pereche de numere u v, decriind o muchie a multigrafului, cu extremitatile in nodurile u si v.
Date de iesire
In fisierul de iesire ciclueuler.out veti tipari M numere x1 x2 ... xM, cu proprietatea ca (x1,x2), (x2,x3), ..., (xM,x1) sunt muchiile ciclului Eulerian determinat, sau numarul -1, in cazul in care G nu este Eulerian.
Restrictii
- 1 ≤ N ≤ 100 000
- 1 ≤ M ≤ 500 000
- Solutia nu este unica; orice solutie valida va primi punctajul maxim.
Exemplu
| ciclueuler.in | ciclueuler.out |
|---|---|
| 4 6 1 2 1 3 2 2 2 3 3 4 3 4 | 1 2 2 3 4 3 |
Explicatie
Ciclul format din muchiile (1,2), (2,2), (2,3), (3,4), (4,3), (3,1), in aceasta ordine, este un ciclu Eulerian.
Solutie
Conform unei teoreme datorate lui Leonhard Euler, un multigraf este Eulerian (admite un ciclu Eulerian) daca si numai daca este conex si toate nodurile sale au grad par (exista unele lucrari care definesc proprietatea Euleriana pe baza acestei teoreme, insa, indiferent de modalitatea de abordare aleasa de autori, rezultatul final cu privire la aceste structuri ramane acelasi). Pentru a construi un ciclu Eulerian putem folosi urmatoarele variante:
- Generam toate ciclurile simple ale multigrafului (spre exemplu, folosind metoda backtracking) si verificam proprietatea Euleriana. O astfel de abordare are, insa, complexitate exponentiala in raport cu dimensiunea datelor de intrare si o consideram lipsita de utilitate practica.
- Folosind algoritmul lui Fleury, pornim de la un nod oarecare si, la fiecare pas, parcurgem o muchie a carei stergere din graf nu l-ar deconecta. Stergem muchia respectiva si, deplasandu-ne in celalalt capat al ei, continuam algoritmul in aceeasi maniera pana cand vom epuiza toate muchiile grafului. Ciclul obtinut este Eulerian.
Pentru implementarea algoritmului lui Fleury, putem face o parcurgere in adancime din nodul de start, etichetand muchiile dupa tipul lor (muchii de arbore si muchii de intoarcere). La fiecare pas in construirea ciclului, vom alege intotdeauna muchiile de intoarcere inaintea muchiilor de arbore. Implementata cu grija, aceasta solutie are complexitate liniara. - O alta solutie se foloseste de faptul ca orice graf Eulerian poate fi descompus ca reuniune de cicluri disjuncte. Astfel, algoritmul formeaza un ciclu oarecare, parcurgandu-l apoi in ordine inversa pentru a intercala recursiv ciclurile formate de muchiile ramase in graf. Vom prezenta succint algoritmul in pseudocod:
euler (nod v)
cat timp (v are vecini)
w = un vecin aleator al lui v
sterge_muchie (v, w)
euler (w)
sfarsit cat timp
adauga v la cicluAceasta abordare recursiva este foarte simpla si usor de implementat, cu toate ca, pentru grafuri de dimensiuni mari, va conduce la probleme de stack overflow. Din aceata cauza, recomandam implementarea iterativa a algoritmului, folosind o stiva gestionata manual pentru a retine nodurile din ciclul format. O solutie ce urmareste aceasta idee se afla aici.
Exista mai multe extensii ale ultimei solutii prezentate. Ideea algoritmului poate fi aplicata cu succes si in cazul gasirii unui lant Eulerian. In cazul acesta, multigraful trebuie sa contine exact doua noduri de grad impar, care vor fi nodurile de inceput si sfarsit ale lantului. Pentru determinarea lantului, vom adaugata fictiv o muchie intre aceste doua noduri, dupa care vom aplica algoritmul de determinare a unui ciclu Eulerian. Eventual, acest ciclu determinat va fi 'rupt' in locul in care apare muchia adaugata si tiparit in ordinea corecta.
Dupa aceeasi idee putem construi algoritmi pentru a gasi drumuri si circuite Euleriene in grafuri orientate. Aici, criteriul de existenta pentru un circuit Eulerian este ca fiecare nod sa aiba gradul interior (numarul arcelor care 'intra' in acel nod) egal cu cel exterior (numarul arcelor care 'ies' din nod), iar pentru drum Eulerian sa existe exact doua noduri, unul cu gradul exterior cu 1 mai mare decat cel interior, iar celalalt cu gradul interior cu 1 mai mare decat cel exterior; primul nod va actiona ca punct de plecare, iar celalalt ca punct de sosire pentru drum.
Aplicatii
Incepand cu Problema podurilor din Konigsberg, studiul lanturilor Euleriene in grafuri si-a gasit numeroase aplicatii. In matematica distractiva apar figuri asemanatoare celor de mai jos, punandu-se problema desenarii lor fara a ridica creionul de pe hartie si fara a desena de mai multe ori aceeasi linie.
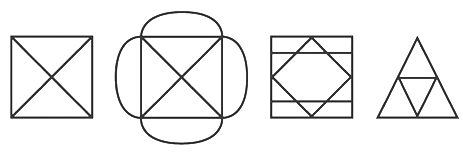
Raspunsul unor astfel de probleme se obtine simplu prin transformarea retelei respective intr-un graf si testarea proprietatii Euleriene.
De asemenea, o alta aplicatie interesanta este studiul drumurilor si circuitelor Euleriene in grafuri de Bruijn. O problema care se poate rezolva cu ajutorul acestor notiuni este Biti.
Alte probleme care folosesc in rezolvare ideea drumurilor Euleriene sunt:
- Domino
- Johnie
- Tester
- Winning Checkers
- Bridges Painting
- Strange Graph
- Ancient Decoration
- Depot Rearrangement, CEOI 2005
 Poti vedea testele pentru aceasta problema accesand
Poti vedea testele pentru aceasta problema accesand 