Solutii Junior Challenge 2021
- Lista de probleme
- Perrynator
- Veverite
- PWCA
- Rollercoaster
- Aglet
- Capcana
Solutia problemei Perrynator
Subtask 1: shiftarea se face doar la dreapta:
Facem mereu query cu o singura pozitie unde nu stim ce valoare e, apoi simulam shiftarea.
Subtask 2: n ≤ 4:
Pentru n ≤ 3 putem considera ca shiftarea se face doar la dreapta, deoarece ambele directii rezulta in aceeasi permutare.
pentru n = 4, pot exista mai multe solutii, una din ele este:
Initial aflam pozitia lui 4: Sa zicem ca momentan stim valoarea de pe o anumita pozitie, putem face query-uri de cate doua elemente cu pozitia asta si fiecare dintre celelalte, avand grija la swap-uri, iar cand raspunsul unui query este egal cu valoarea cunoscuta, inseamna ca am gasit o valoare mai mare pe care o putem afla cu un query doar pe acea pozitie. Putem repeta asta, pana cand gasim pozitia lui 4.
Dupa ce am aflat pozitia lui 4, putem face query cu 4 si fiecare dintre celelalte pozitii, tinand cont de swap-uri, pentru a afla toata permutarea.
Pentru 60-70 de puncte:
O solutie, cu numar mai mare de query-uri este aceea de a afla permutarea incepand cu cele mai mari valori, descrescator.
Cand cunoastem pozitiile celor mai mari k valori, facem query-uri cu toate aceste pozitii, si o alta pozitie aleasa aleator, pana cand gasim pe ce pozitie se afla al (k+1)-lea cel mai mare element.
Aceasta solutie face aproximativ N2/2 query-uri.
Pentru 100 de puncte:
Vom considera n > 3.
Initial, gasim pe ce pozitie se afla valoarea 1:
Putem cauta binar pozitia pe care se afla 1, pentru a verifica daca 1 este intr-un anumit interval, facem query cu toate pozitiile care nu sunt incluse in acel interval, astfel, daca raspunsul este diferit de 1, inseamna ca pozitia lui 1 se afla in acest interval, iar daca este 1, stim ca pozitia e in afara, si ca aceasta nu s-a schimbat.
Dupa ce stim valorile de pe un subset de pozitii, una din valori fiind 1, pentru a afla o noua valoare facem urmatorii pasi:
- Query pe o singura pozitie pe care nu o cunosteam, pentru a afla o noua valoare.
- Dupa acest query, noua permutare are 2 variante posibile. Pentru a afla in ce varianta ne aflam, e suficient sa aflam pe ce pozitie se afla 1, care la randul lui are 2 pozitii posibile pe care poate fi. Facand un query cu toate pozitiile mai putin una din acestea 2, putem afla daca valoarea 1 se afla pe acea pozitie, sau nu, fara a schimba deloc permutarea curenta. Astfel, odata ce am aflat in ce directie s-a shiftat 1, putem afla pozitiile tuturor valorilor pe care le stiam inainte, impreuna cu o valoare noua din query-ul precedent.
Putem repeta acesti doi pasi, pentru a afla toate elementele permutarii, unul cate unul, efectuand cate doua query-uri pentru fiecare valoare nou aflata.
Astfel, numarul final de query-uri este log(N) + 2*(n-2) = 203 query-uri, deoarece ne putem oprii odata ce am aflat n-1 valori.
Solutia problemei Veverite
Subtaskul 1: N,Q ≤ 2000
O soluţie greedy uşor de intuit ar fi ca pentru fiecare query să parcurgem şirul de la stânga la dreapta şi să menţinem un set cu elementele pe care nu le-am adăugat încă la suma totală. În momentul când întâlnim un "blocaj" (adică suma este mai mică strict decât valoarea de la pasul curent) extragem din setul de elemente maximul până când se respectă restricţia din nou. După ce am rezolvat blocajul îl adaugăm şi pe el în set şi trecem mai departe.
Deoarece elemente din vector sunt în ordine crescătoare, extragerea elementului maxim şi adăugarile pot fi simulate uşor cu ajutorul unei stive.
Complexitate: O(N * Q)
Subtaskul 2: Ai ≤ 100, pentru 1 ≤ i ≤ N, N,Q ≤ 105
Se observă că pentru query-urile mai mari decât 100, răspunsul va fi clar 0. Putem precalcula răspunsul pentru fiecare valoare iniţială posibilă de la 1 la 100 folosind soluţia anterioară şi să răspundem la query-uri în O(1).
Complexitate: O(N * valmax + Q)
Subtaskul 3: 1 ≤ N, Q ≤ 105, 1 ≤ Ai ≤ 109
Observaţie: Pentru un vector există maxim 2 * log(valmax) blocaje.
Demonstraţie: Pentru oricare 3 elemente adiacente din şirul de elemente pe care le vom considera "blocaje" se împlineşte următoarea inegalitate:
a * 2 < c (unde a, b şi c sunt cele 3 elemente), deoarece la pasul în care ne-am blocat în b am adăugat cel puţin un element mai mare sau egal decât a la sumă (întrucât şi a se afla la acel moment în set). Astfel, la fiecare 2 elemente suma se dublează, ceea ce înseamnă că în 2 * log(valmax) paşi îşi va atinge valoarea maximă. Dacă menţinem setul necesar în greedy ca o listă de intervale de valori nefolosite putem procesa mult mai rapid şirul. Căutam binar poziţia primului blocaj şi adaugăm în listă intervalul de elemente până la acel blocaj. Pentru a simula procesul de extragere de maxim din set de un număr repetat de ori, verificăm dacă trebuie să adaugăm complet ultimul interval din listă. Dacă da, atunci îl adaugăm şi trecem mai departe, altfel căutam binar cât este necesar să adaugăm din el. Apoi căutam binar poziţia următorului blocaj şi tot aşa mai departe până am procesat tot.
Complexitate finală: O(N * log(valmax) * log(N))
Solutia problemei PWCA
Mai întâi trebuie să facem câteva observaţii legate de transformare:
Observaţia 1:
Fie două şiruri A şi B astfel încât A poate deveni B. Să presupunem că Bi ≠ Bi+1 pentru un anumit i. Atunci Ai = Bi şi Ai+1 = Bi+1 (Ai ≠ Ai+1). Această proprietate se demonstrează astfel:
- Dacă Ai = Ai+1 atunci acestea nu pot deveni diferite.
- Dacă Ai ≠ Bi şi Ai+1 ≠ Bi+1 atunci ambele valori vor trebui modificate pe parcursul transformării. Cele două modificări se vor face în mod evident pe rând, iar după prima dintre ele, cele două valori vor deveni egale. Aşa cum am văzut şi mai sus, dacă două valori vecine devin egale, atunci nu vor mai putea fi diferite (aşa cum vor trebui să fie la final).
Observaţia 2:
Folosind observaţia 1, ne dăm seama că putem rezolva secvenţele maximale ale lui B independent. Astfel, problema se reduce la a găsi numărul de şiruri A care pot fi transformate într-un şir de valori egale cu 0 sau 1 de o anumită lungime (cele două cazuri sunt identice).
Greedy:
Acum putem veni cu un algoritm greedy care verifică dacă un şir iniţial A poate fi transformat într-unul plin de 1. Ideea de la care plcăm este cea de a transforma subsecvenţele de 0 în 1 de fiecare dată când avem ocazia. Astfel, putem porni cu o stivă de la stânga la dreapta în care introducem pe rând secvenţele de valori egale din A. Acum, vom urmări două cazuri:
- În vârful stivei se află o secvenţă de 0 mai mică sau egală cu cea precedentă. O transformăm într-una de 1 şi actualizăm stiva.
- În vârful stivei se află o secvenţă de 1 care permite secvenţei precedente (de 0) să se transforme. Efectuăm transformarea şi actualizăm stiva.
Mereu după ce actualizăm stiva verificăm din nou cele două cazuri. Acest algoritm are complexitatea O(|A|).
Subtask 1 (10 puncte)
Pentru acest subtask vom considera toate şirurile iniţiale A posibile. Pentru a verifica un şir iniţial, împărţim şirul B în subsecvenţe de valori egale şi aplicăm algoritmul greedy de mai sus pentru secvenţele din A corespunzătoare celor din B. Complexitatea timp este O(2|B| ⋅ |B|).
Subtask 2 (20 de puncte)
Putem îmbunătăţii soluţia precedentă precalculând pentru fiecare l de la 1 la VMAX numărul de şiruri iniţiale A pentru care se poate ajunge la un şir de valori egale cu 0 sau 1 de lungime l. Complexitate timp O(2VMAX ⋅ VMAX + N).
Subtask 3 (30 de puncte)
Pentru a continua avem nevoie de o soluţie total diferită. Să considerăm că vrem să transformăm şirul A într-un şir de valori egale cu 1. Fie S secvenţa de lungime maximă din A. Avem două cazuri:
- S este formată din valori de 1. În acest caz, ştim că toate secvenţele de 0 nu sunt mai lungi decât S. Iniţial, S va avea câte o secvenţă de 0 la stânga şi la dreapta (sau nu, dacă este lângă margine). Deoarece aceste secvenţe nu sunt mai lungi decât S, ele pot fi transformate în 1. Astfel, vom extinde S la stânga şi la dreapta. În acelaşi timp, secvenţele de 1 care erau vecine cu cele de 0 se vor alipi şi ele. Acum S este mai mare şi se poate extinde din nou în acelaşi mod. Am demonstrat că în acest caz şirul A poate fi transformat.
- S este formată din valori de 0. Acest caz este mai greu deoarece vom vrea ca la un moment dat să îl transformăm pe S în 1 cu ajutorul unei secvenţe mai mari de 1. Această secvenţă T se poate forma la stânga sau la dreapta de S. Acum vom demonstra că dacă această secvenţă se poate forma, atunci poate continua până când umple tot spaţiul de la stânga lui S. Ştim că odată formată, T este mai mare decât S, şi în acelaşi timp mai mare decât toate restul secvenţelor de 0 deoarece acestea nu vor creşte niciodată faţă de lungimea iniţială (pentru că nu este optim). Ştiind asta, putem considera că T poate transforma tot spaţiul de la stânga lui S în 1. Odată ce set întâmplă asta, S se transformă în 1 (fiind lângă T) şi începe să se extindă în direcţia opusă ca în subtask-ul anterior.
Aşadar, în cazul al doilea ne-am dat seama că fie tot ce este la stânga de S, fie tot ce este la dreapta se va transforma în 1. Acum vom construi o soluţie folosind programare dinamică:
- cntAll[len][k][lval][rval] = numărul de şiruri de lungime len, cu secvenţa maximă de lungime k, cu primul element lval şi ultimul element rval (lval şi rval sunt valori binare).
- cntFull[len][k][lval][rval] = numărul de şiruri de lungime len, cu secvenţa maximă de lungime k, cu primul element lval şi ultimul element rval (lval şi rval sunt valori binare) care se pot transforma într-un şir plin de 1.
- cntAllPref[len][k][lval][rval] = numărul de şiruri de lungime len, cu secvenţa maximă de lungime maxim k, cu primul element lval şi ultimul element rval (lval şi rval sunt valori binare).
- cntFullPref[len][k][lval][rval] = numărul de şiruri de lungime len, cu secvenţa maximă de lungime maxim k, cu primul element lval şi ultimul element rval (lval şi rval sunt valori binare) care se pot transforma într-un şir plin de 1.
cntAllPref şi cntFullPref sunt uşor de calculat fiind doar sume pe prefixe (ale parametrului k) pentru dinamicile principale (cntAll şi cntFull).
Pentru recurenţe va trebui să fixăm poziţia secvenţei maximale (de lungime k). Pentru fiecare poziţie de început pos avem următoarea recurenţă (vom folosi notaţiile lLen = pos - 1 şi rLen = len - (pos+k-1)):
- Pentru cazul în care ce mai lungă secvenţă este de 0:
- cntAll[len][k][lval][rval] += cntAllPref[lLen][k-1][lval][1] ⋅ cntAllPref[rLen][k][1][rval]
- cntFull[len][k][lval][rval] += cntFullPref[lLen][k-1][lval][1] ⋅ cntAllPref[rLen][k][1][rval], dacă lLen ≥ len
- cntFull[len][k][lval][rval] += cntAllPref[lLen][k-1][lval][1] ⋅ cntFullPref[rLen][k][1][rval], dacă rLen ≥ len
- cntFull[len][k][lval][rval] += cntFullPref[lLen][k-1][lval][1] ⋅ cntFullPref[rLen][k][1][rval], dacă lLen ≥ len şi rLen ≥ len
- Pentru cazul în care ce mai lungă secvenţă este de 1:
- cntAll[len][k][lval][rval] += cntAllPref[lLen][k-1][lval][0] ⋅ cntAllPref[rLen][k][0][rval]
- cntFull[len][k][lval][rval] += cntAllPref[lLen][k-1][lval][0] ⋅ cntAllPref[rLen][k][0][rval]
Pentru a număra şirurile A care pot fi transformate în şiruri de valori egale cu 1 sau 0 vom avea complexitatea O(|A|3). Cum N = 1, asta înseamnă O(VMAX3).
Subtask 4 (40 de puncte)
Pentru acest subtask se va folosi soluţia anterioară pentru a precalcula răspunsul pentru toate lungimile l de la 1 la VMAX (asemănător cu subtask-ul 2). Complexitate timp O(VMAX3).
Soluţia de 100 de puncte se găseşte aici.
Solutia problemei Rollercoaster
Subtask 1 (20 de puncte) - N ≤ 15
Pentru acest subtask se pot genera si verifica toate configuratiile de roller-coastere.
Complexitate timp: O(2N*N)
Complexitate spatiu: O(N)
Subtask 2 (20 + 20 de puncte) - N ≤ 1000
Pentru acest subtask este nevoie sa ne gandim la solutii de programare dinamica.
Prima idee care ne vine este:
dp[i] = coeficientul maxim de distractie al unui roller-coaster si se termina cu turnul i
Relatia de recurenta va fi:
dp0 = 0
dp[i] = max {dp[j] + cmmdc (a[j], a[i])| 0 <= j < i}
In acelasi timp mai tinem si:
cnt[i] = numarul de roller-coastere care au coeficient maxim de distractie si se termina cu turnul i
Complexitate timp: O(N2)
Complexitate spatiu: O(N)
Subtask 3 (20 + 20 + 60 de puncte) - N ≤ 250.000
Pentru punctaj maxim este nevoie sa exploatam operatia de cmmdc.
Vom crea o alta dinamica care nu tine cont de indicii turnurilor, dar va tine cont de divizorii inaltimilor.
dp[d] = coeficientul maxim de distractie al unui roller-coaster si se termina cu un turn cu inaltimea multiplu de d
Recurenta nu este foarte grea. Vom avea pentru fiecare turn i o variabila auxiliara best:
best = max{dp[d] + d| d este divizor al inaltimii turnului i}
Dupa vom actualiza dp-urile folosindu-ne de best:
dp[d] max= best unde d este divisor al inaltimii turnului i
Adaugarea vectorului cnt pentru aflarea numarului de solutii (cnt[d] = numarul de roller-coastere care au coeficient maxim de distractie si se termina cu un turn cu inaltime multiplu de d) se va face ca la solutia de 40p.
Complexitate timp: O(N*sqrt(MAXVAL))
Complexitate spatiu: O(MAXVAL + N)
Solutia problemei Aglet
Deoarece noi incercam sa minimizam timpul worstcase ar trebui sa avem o strategie determinista. O strategie ar consta intr-o schema fixata in care stim ca daca am determinat ca setul de şireturi posibile este S atunci ar trebui sa intrebam daca şiretul target se afla in S' (un subset al lui S).
Subtaskul 1 (20 de puncte):
O solutie de complexitate O(3N) se bazeaza pe urmatoarea dinamica:
dp[mask] = care este timpul minim in care rezolvam problema daca stim ca şiretul target se afla in setul reprezentat de mask.
Dinamica prezentata poate fi calculata iterand prin fiecare submasca mask2 a lui mask si prin a testa daca ar fi optim sa verificam daca şiretul target apartine lui mask2 sau nu. Recurenta rezulta in felul urmator:
![dp[mask] = min(dp[mask], \;max(dp[mask_2], \;dp[mask \oplus mask_2]) + t) \; \forall \; mask_2 \subset mask dp[mask] = min(dp[mask], \;max(dp[mask_2], \;dp[mask \oplus mask_2]) + t) \; \forall \; mask_2 \subset mask](http://www.infoarena.ro/static/images/latex/c286b3bc856e764501968919addef2f3_3.5pt.gif)
Pentru 70 de puncte:
Exista insa o perspectiva mai buna, sa alegem cate 2 şireturi posibile si sa le combinam intr-un "şiret echivalent". Adica daca avem 2 şireturi care dureaza fiecare cate A, respectiv B secunde sa le punem, le putem combina intr-un şiret echivalent care dureaza 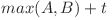 secunde. Este clar ca urmand procedeul de mai sus tot ce facem e sa construim strategia de jos in sus. Dar cum alegem ce şireturi sa punem mai intai?
secunde. Este clar ca urmand procedeul de mai sus tot ce facem e sa construim strategia de jos in sus. Dar cum alegem ce şireturi sa punem mai intai?
Aici putem pur si simplu alege in mod greedy cele mai "rapide" (care dureaza cel mai putin) 2 şireturi si sa le combinam pe ele. O demonstratie posibila a acestui greedy este urmatoarea:
- Numim "şiret artificial" un şiret care nu exista la inceput si de fapt reprezinta un subset de şireturi obtinut prin procedeul de mai sus. Sa notam cele mai rapide 2 şireturi cu X si Y.
- Sa presupunem ca X este prima data combinat cu un "şiret artificial". Acel şiret artificial trebuie sa fi fost obtinut si el la randul sau prin multiple combinari, sa numim şireturile din prima astfel de operatie A si B. Insa noi putem obtine o solutie cel putin la fel de buna daca schimbam X si A intre ei.
- Astfel, putem presupune ca X este combinat cu un şiret care nu este artificial. Analog, putem presupune ca si Y este combinat cu un şiret care nu este artificial. Sa presupunem ca X este combinat cu un şiret A, iar Y este combinat cu un şiret B. (presupunem prin simetrie ca B dureaza mai mult decat A si implicit faptul ca X si Y sunt minimele globale si, astfel, mai mult si decat ele).
- Atunci am putea da swap lui A cu Y si am obtine o solutie cel putin la fel de buna ca cea anterioara.
- Astfel, am demonstrat ca putem combina cele mai ieftine 2 şireturi fara sa avem regrete.
In concluzie, la fiecare pas alegem cele mai rapide 2 şireturi, le combinam intr-un şiret artificial si il adaugam inapoi in multimea noastra. O structura de date care ne poate ajuta sa facem aceste operatii este un heap in O(log2N). Deoarece facem N astfel de operatii, complexitatea finala va fi O(N * log2N).
Pentru 100 de puncte:
Putem sa ne folosim de faptul ca mereu cand combinam 2 sireturi obtinem unul mai "lent" decat tot ce am mai obtinut pana acum. Putem deci sa simulam aceste operatii folosind 2 cozi. Complexitate finala O(N).
Acest Şmen Aceasta strategie finala si optimizare de la heap la 2 cozi poate parea asemanatoare cu algoritmul de gasit Coduri Huffman.
Solutia problemei Capcana
Observaţia 1: Din 2 * K + 1 ≤ N putem deduce că plăcuţele normale sunt mai numeroase decât cele periculoase.
O primă soluţie care foloseşte N - 1 queryuri ar compara plăcuţa 1 cu fiecare din celelalte şi ar nota pentru fiecare plăcuţă dacă este de acelaşi tip sau nu cu prima.
Ştim că plăcuţele care apartin tipului mai numeros sunt cele normale.
Observaţia 2: Putem identifica o plăcuţă normală prin 2 * K + 1 queryuri dacă aplicăm strategia de mai sus primelor 2 * K + 1 plăcuţe.
Observaţia 3: Dacă cunoaştem un interval de plăcuţe normale de lungime len atunci noi putem identifica prima plăcuţă periculoasă dintr-un alt interval de lungime maxim len în log(len) queryuri.
În acest caz noi putem folosi o căutare binară pentru a găşi plăcuţa periculoasă.
Să spunem că la un anumit moment de timp cunoaştem tipul fiecărei plăcuţe dintr-un anumit prefix care se termină cu un interval de placuţe normale. Procedăm astfel:
- Pasul 1: Dăm query după intervalul de placuţe normale şi intervalul de aceeaşi lungime aflat imediat după acesta.
- Pasul 1.1: Dacă am obţinut că au acelaşi număr de plăcuţe periculoase (adică 0) atunci ne extindem prefixul şi intervalul de plăcuţe normale, iar apoi revenim la pasul 1 cu noul interval de placuţe normale.
- Pasul 1.2: Altfel, ştim că în intervalul nou testat se află una sau mai multe plăcuţe periculoase. Putem să o aflam pe prima dintre ele folosindu-ne de strategia de la observaţia 3.
- Pasul 2: După ce am identificat plăcuţa periculoasă dăm query după intervalul nostru de placuţe normale şi intervalul care urmează imediat după plăcuţa periculoasă găsită.
- Pasul 2.1: Dacă acest query ne transmite că şi al doilea interval are doar plăcute normale atunci putem relua procesul de la pasul 1
- Pasul 2.2: Dacă în schimb aflăm că şi acest interval conţine una sau mai multe plăcuţe periculoase, ne folosim din nou de observaţia 3 pentru a o găşi pe prima dintre ele, revenind practic la pasul 1.2.
Câte queryuri foloseşte soluţia prezentată mai sus?
2 * K - 1(că să descopere prima plăcuţă normală) +
log(N) (îşi dublează intervalul de placuţe normale lungimea) +
K (când transferăm intervalul de plăcuţe normale din interior la final, notat cu pasul 2.1 în explicaţie) +
K * log (de fiecare dată când descoperim o plăcuţa normală o căutăm binar)
