Solutia problemei Aglet
Deoarece noi incercam sa minimizam timpul worstcase ar trebui sa avem o strategie determinista. O strategie ar consta intr-o schema fixata in care stim ca daca am determinat ca setul de şireturi posibile este S atunci ar trebui sa intrebam daca şiretul target se afla in S' (un subset al lui S).
Subtaskul 1 (20 de puncte):
O solutie de complexitate O(3N) se bazeaza pe urmatoarea dinamica:
dp[mask] = care este timpul minim in care rezolvam problema daca stim ca şiretul target se afla in setul reprezentat de mask.
Dinamica prezentata poate fi calculata iterand prin fiecare submasca mask2 a lui mask si prin a testa daca ar fi optim sa verificam daca şiretul target apartine lui mask2 sau nu. Recurenta rezulta in felul urmator:
![dp[mask] = min(dp[mask], \;max(dp[mask_2], \;dp[mask \oplus mask_2]) + t) \; \forall \; mask_2 \subset mask dp[mask] = min(dp[mask], \;max(dp[mask_2], \;dp[mask \oplus mask_2]) + t) \; \forall \; mask_2 \subset mask](http://www.infoarena.ro/static/images/latex/c286b3bc856e764501968919addef2f3_3.5pt.gif)
Pentru 70 de puncte:
Exista insa o perspectiva mai buna, sa alegem cate 2 şireturi posibile si sa le combinam intr-un "şiret echivalent". Adica daca avem 2 şireturi care dureaza fiecare cate A, respectiv B secunde sa le punem, le putem combina intr-un şiret echivalent care dureaza 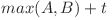 secunde. Este clar ca urmand procedeul de mai sus tot ce facem e sa construim strategia de jos in sus. Dar cum alegem ce şireturi sa punem mai intai?
secunde. Este clar ca urmand procedeul de mai sus tot ce facem e sa construim strategia de jos in sus. Dar cum alegem ce şireturi sa punem mai intai?
Aici putem pur si simplu alege in mod greedy cele mai "rapide" (care dureaza cel mai putin) 2 şireturi si sa le combinam pe ele. O demonstratie posibila a acestui greedy este urmatoarea:
- Numim "şiret artificial" un şiret care nu exista la inceput si de fapt reprezinta un subset de şireturi obtinut prin procedeul de mai sus. Sa notam cele mai rapide 2 şireturi cu X si Y.
- Sa presupunem ca X este prima data combinat cu un "şiret artificial". Acel şiret artificial trebuie sa fi fost obtinut si el la randul sau prin multiple combinari, sa numim şireturile din prima astfel de operatie A si B. Insa noi putem obtine o solutie cel putin la fel de buna daca schimbam X si A intre ei.
- Astfel, putem presupune ca X este combinat cu un şiret care nu este artificial. Analog, putem presupune ca si Y este combinat cu un şiret care nu este artificial. Sa presupunem ca X este combinat cu un şiret A, iar Y este combinat cu un şiret B. (presupunem prin simetrie ca B dureaza mai mult decat A si implicit faptul ca X si Y sunt minimele globale si, astfel, mai mult si decat ele).
- Atunci am putea da swap lui A cu Y si am obtine o solutie cel putin la fel de buna ca cea anterioara.
- Astfel, am demonstrat ca putem combina cele mai ieftine 2 şireturi fara sa avem regrete.
In concluzie, la fiecare pas alegem cele mai rapide 2 şireturi, le combinam intr-un şiret artificial si il adaugam inapoi in multimea noastra. O structura de date care ne poate ajuta sa facem aceste operatii este un heap in O(log2N). Deoarece facem N astfel de operatii, complexitatea finala va fi O(N * log2N).
Pentru 100 de puncte:
Putem sa ne folosim de faptul ca mereu cand combinam 2 sireturi obtinem unul mai "lent" decat tot ce am mai obtinut pana acum. Putem deci sa simulam aceste operatii folosind 2 cozi. Complexitate finala O(N).
Acest Şmen Aceasta strategie finala si optimizare de la heap la 2 cozi poate parea asemanatoare cu algoritmul de gasit Coduri Huffman.
