Solutii Summer Challenge 2021

Solutia problemei Petreceri

Subtask 1:

Se observa ca mereu este optim consumul celei mai ieftine unităţi de lapte care poate fi adusă la o petrecere.

O observaţie importantă pentru soluţia finala a problemei poate fi dedusă dacă se redefineşte achiziţionarea unei noi unităţi. Nu face nicio diferenţa dacă pentru o sticlă de lapte se plăteşte înainte de a o consuma sau la petrecerea de unde a fost cumpărată. Astfel se pot ţine minte cele mai bune preţuri ale unităţilor de lapte la care are Rick acces în fiecare moment şi se va adaugă la rezultat doar cantitatea băută. Când se ajunge la o noua petrecere se vor arunca toate unităţile mai scumpe decât cele vândute acolo, se vor consuma din cele mai ieftine a[i] unităţi(completând cu băuturi se cost c[i] dacă e necesar) şi se vor înlocui unităţile dispărute cu unităţi de preţ c[i]. Greedy-ul este corect deoarece nu merită sa se consume o unitate de lapte mai scumpă dacă altele mai ieftine pot fi luate. Pentru asta se poate folosi o coada(deque).
Deoarece fiecare unitate consumata trebuie considerata şi rămân t unităţi complexitatea este O(t+\sum_{i=1}^{n} a[i]) \equiv O(n\cdot t) . 

Subtask 2:

Pentru 30 de puncte se pot parcurge petrecerile în ordine crescătoare a preţurilor şi se vor transporta mai multe unităţi de lapte către petrecerile care urmează. Pentru a face asta se va tine minte, pentru fiecare petrecere, T[i], numărul maxim de unităţi de lapte pe care le mai poate duce Rick către petrecerea i+1. Astfel, pentru fiecare petrecere se vor modifica succesorii dacă permite şirul T.

Subtask 3:

La soluţia primului subtask se observa ca nu este necesara stocarea fiecărei unităţi în parte ci se poate tine minte frecventa unităţilor cu acelaşi preţ. Operaţiile de mai sus se pot face cu un set de perechi de tip (valoare, frecventa). Complexitatea noua este 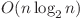O(n \log_2{n}) .

Subtask 4:

Operaţiile făcute în soluţia anterioara cu un set(găsirea şi eliminarea maximelor şi a minimelor si adăugarea de elemente mai mari decât toate celelalte considerate) se pot face cu o coadă cu operaţii la ambele capete(deque). Unităţile şi frecvenţele lor vor fi reţinute în ordinea crescătoare a preţurilor.
Complexitatea finală este 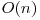O(n) .

Solutia problemei Transform3

Soluţia cu 2N + 2QlogN muchii

Peste şirul iniţial de lungime N generăm un arbore de intervale. Nodurile interne vor avea valori începând de la N+Q+1 (pentru că nodurile de la N+1 la N+Q sunt rezervate pentru rezolvarea restricţiilor problemei). Pentru N = 10 şi Q = 5, un exemplu de arbore de intervale este:

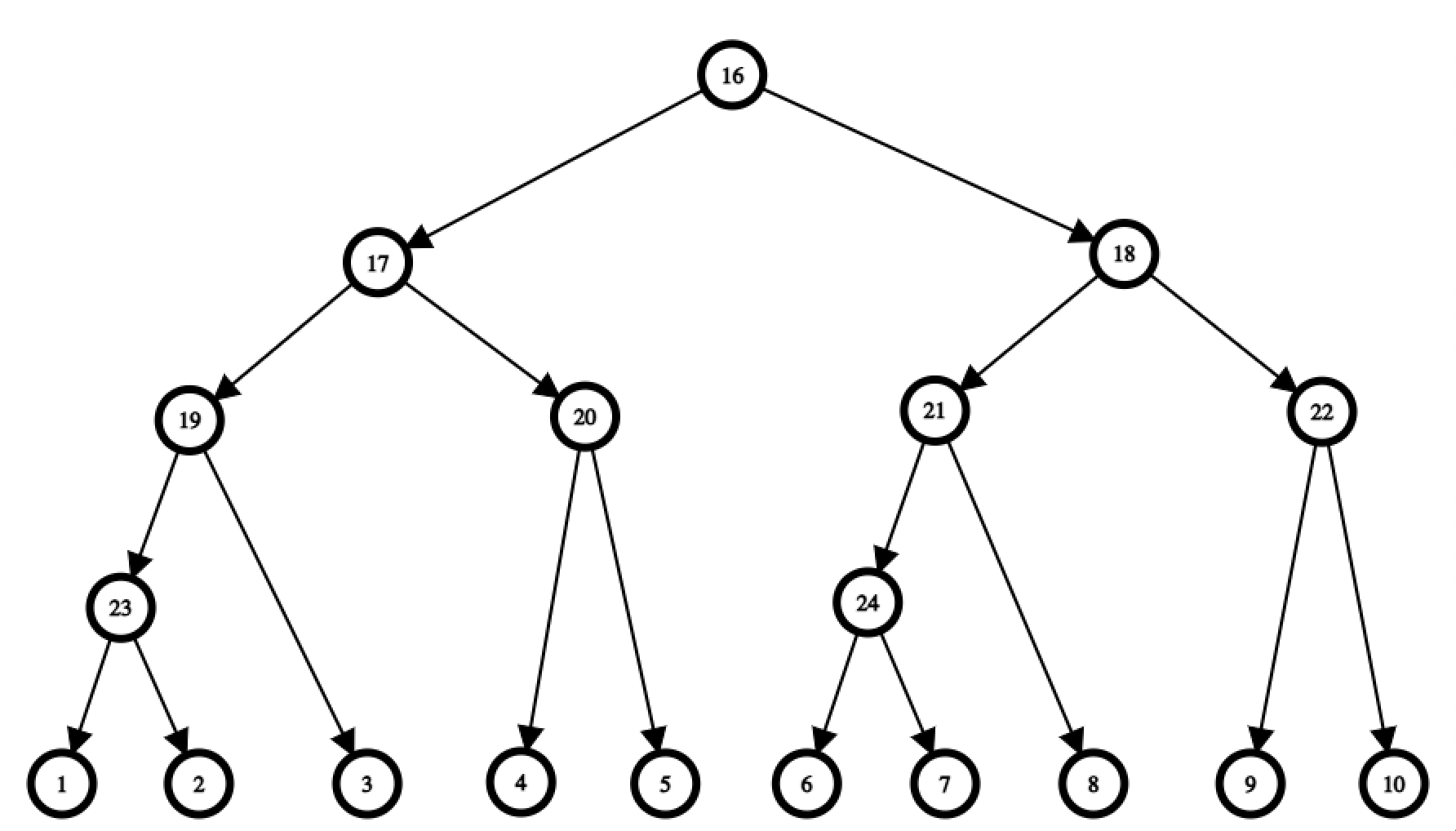
Până acum am folosit 2N muchii (deoarece un arbore de intervale construit peste un şir de lungime N are lungimea maxim 2N).

Pentru rezolvarea unei restricţii, putem să ne folosim de acest arbore de intervale astfel: ştim că orice interval 1 ≤ L ≤ R ≤ N poate fi acoperit cu maxim 2logN alte sub-intervale corespunzătoare unor noduri ale arborelui. Astfel, pentru fiecare restricţie, putem să tragem maxim 2logN muchii de la nodul corespunzător restricţiei (N+1 ≤ nod ≤ N+Q) la toate nodurile din arborele de intervale de care avem nevoie. De exemplu, dacă [L1, R1] = [2, 6] si [L2, R2] = [3, 9], vom trage următoarele muchii (restul restricţiilor au fost omise pentru claritate). În total vom folosi deci 2N + 2QlogN muchii.

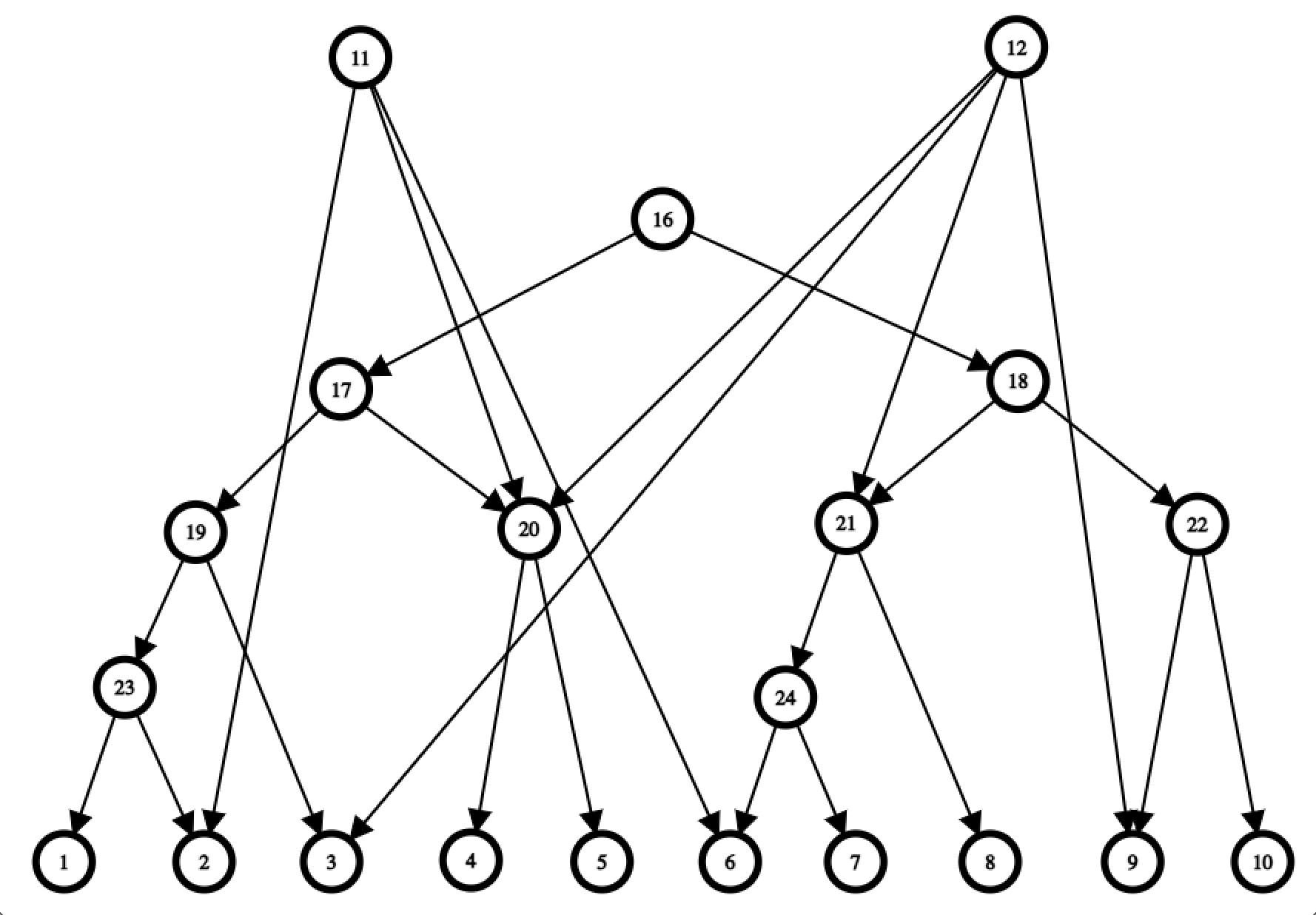
Soluţia cu 4N + 2Q muchii

Pentru a reduce numărul de muchii, trebuie să facem următoarele observaţii:

  • Ideile bazate pe arbori duc în general la complexităţi "logaritmice" (apare un log prin complexitatea finală)
  • Numărul de muchii cerut este 4N + 2Q care nu conţine niciun logaritm (deci este un hint că soluţiile bazate pe arbori nu duc la soluţia dorită)
  • Nicăieri în soluţia precedentă nu ne folosim de proprietatea intervalelor din enunţ.
    Aşadar, în loc să plecăm de la un arbore, vom încerca să plecăm de la o structură "liniară", care în cazul nostru este o "coadă simulată cu 2 stive". Mai concret:

Fiecare interval din cele Q îl vom sparge în alte 2 sub-intervale (un prefix şi un sufix). Aceste 2 sub-intervale le vom retine folosind 2 stive puse una lângă alta. De exemplu o spargere pentru intervalul [4, 11] poate fi:

  • leftStack: 6, 5, 4
  • rightStack: 7, 8, 9, 10, 11.

Pentru fiecare din cele Q intervale date, vom încerca să le spargem în 2, folosindu-ne de informaţia de la intervalul precedent (acolo unde este posibil). Algoritmul simulat pentru intervalele [5, 10], [7, 12], [9, 13], [12, 14], [12, 15], [14, 17] este:

IDIntervalleftStackrightStack
1[5, 10]10, 9, 8, 7, 6, 5-
2[7, 12]10, 9, 8, 711, 12
3[9, 13]10, 911, 12, 13
4[12, 14]14, 13, 12-
5[12, 15]14, 13, 1215

Modul de construcţie prezentat anterior este foarte asemănător cu modul în care este stocat std::deque în memorie şi este un şmen util în informatica de olimpiadă.

Mai departe, observăm că fiecărei stive la un moment dat îi corespunde un interval compact (de exemplu, stivei cu elementele {10, 9, 8, 7} îi corespunde intervalul [7, 10]) şi mai mult, unele intervale sunt incluse in altele (intervalul stivei {10, 9, 8, 7} este inclus în intervalul stivei {10, 9, 8, 7, 6, 5} sau intervalul stivei {11, 12} este inclus în intervalul stivei {11, 12, 13}).

Putem aşadar să atribuim fiecărei stive la un anumit moment de timp câte un interval (identificat printr-un cod unic mai mare strict decât N+Q) iar de la un interval oarecare putem să tragem muchie către cel mai mare interval inclus în interiorul sau (dacă există) şi câte o muchie la toate elementele neacoperite de acesta. În final, pentru fiecare restricţie, vom trage muchii de la nodul său corespunzător din intervalul [N+1, N+Q] la cele maxim 2 stive in care se va sparge intervalul.

Pentru exemplul din enunţ, algoritmul ar arăta cam aşa:

IDIntervalleftStackrightStackcod leftStackcod rightStack
1[1, 3][1, 3]-8-
2[2, 3][2, 3]-9-
3[3, 4][3, 3][4, 4]1011

O ultimă observaţie este necesară pentru a obţine 100 de puncte: observăm ca leftStack[i] poate fi creat doar din leftStack[i + 1] (asta dacă la pasul i+1 intervalul nu este creat din nou), respectiv rightStack[i] poate fi creat din rightStack[i - 1] (dacă exista). Dacă atribuim la fiecare pas un cod unic fiecărei din cele 2 stive la un moment de timp, am obţine 2Q coduri distincte. În schimb, dacă atribuim coduri unice fiecărui interval distinct (cu alte cuvinte, nu atribuim coduri distincte dacă leftStack[i] = leftStack[i + 1] sau rightStack[i] = rightStack[i - 1]), atunci numărul de coduri atribuite se reduce la maxim 2N, maxim N pentru fiecare din cele 2 stive. Demonstraţia este următoarea (demonstrăm pentru leftStack, pentru rightStack se poate demonstra similar): leftStack[i] este fie construit din leftStack[i - 1] eliminând un prefix (schimbăm codul doar dacă acest prefix este nenul), fie reconstruită de la 0. Cum la fiecare pas, capătul stâng al intervalului asociat acestei stive creşte cu cel putin o poziţie, acesta fiind maxim N, numărul de coduri distincte asociate pentru toate stivele leftStack la toate momentele de timp este maxim N.

Solutia problemei Portale

Solutie cu N*(N-1)/2 query-uri:

Intr-o matrice de adiacenta initial marcam toate muchiile ca muchie necunoscuta.
Trecem prin toate cele N*(N-1)/2 muchii posibile si pentru fiecare dintre ele, facem un query, marcam muchia curenta ca muchie care sigur se afla in arbore si, in cazul in care muchia stearsa era o muchie care sigur se afla in arbore, o marcam ca muchie care sigur nu se afla in arbore. btw. exista un easter egg in enuntul problemei portale
In final, cu acest algoritm vom cunoaste toate cele N-1 muchii intrucat dupa ce am facut i query-uri, vom stii despre fiecare dintre primele i muchii daca se afla sau nu in arbore
Aceasta implementare primeste aproximativ 10 puncte, dar poate fi optimizata foarte usor in doua modalitati:

  1. Ne oprim dupa ce stim ca dintre primele i muchii folosite in query-uri, N-1 sunt marcate ca muchie care sigur se afla in arbore - Cu aceasta optimizare, algoritmul merge foarte bine pe subtask-ul cu interactor random, si de aceea primeste aproximativ 35 de puncte.
  2. O alta observatie este faptul ca in momentul in care urmeaza sa facem query cu o muchie intre x si y, daca aceste doua noduri se afla in aceeasi componenta considerand muchiile marcate ca muchie care sigur se afla in arbore atunci putem spune ca muchia intre x si y este o muchie care sigur nu se afla in arbore, si nu mai este necesar sa facem acest query - Cu ambele optimizari, solutia primeste aproximativ 45 de puncte. amogus

Ideea pentru Nlog query-uri:

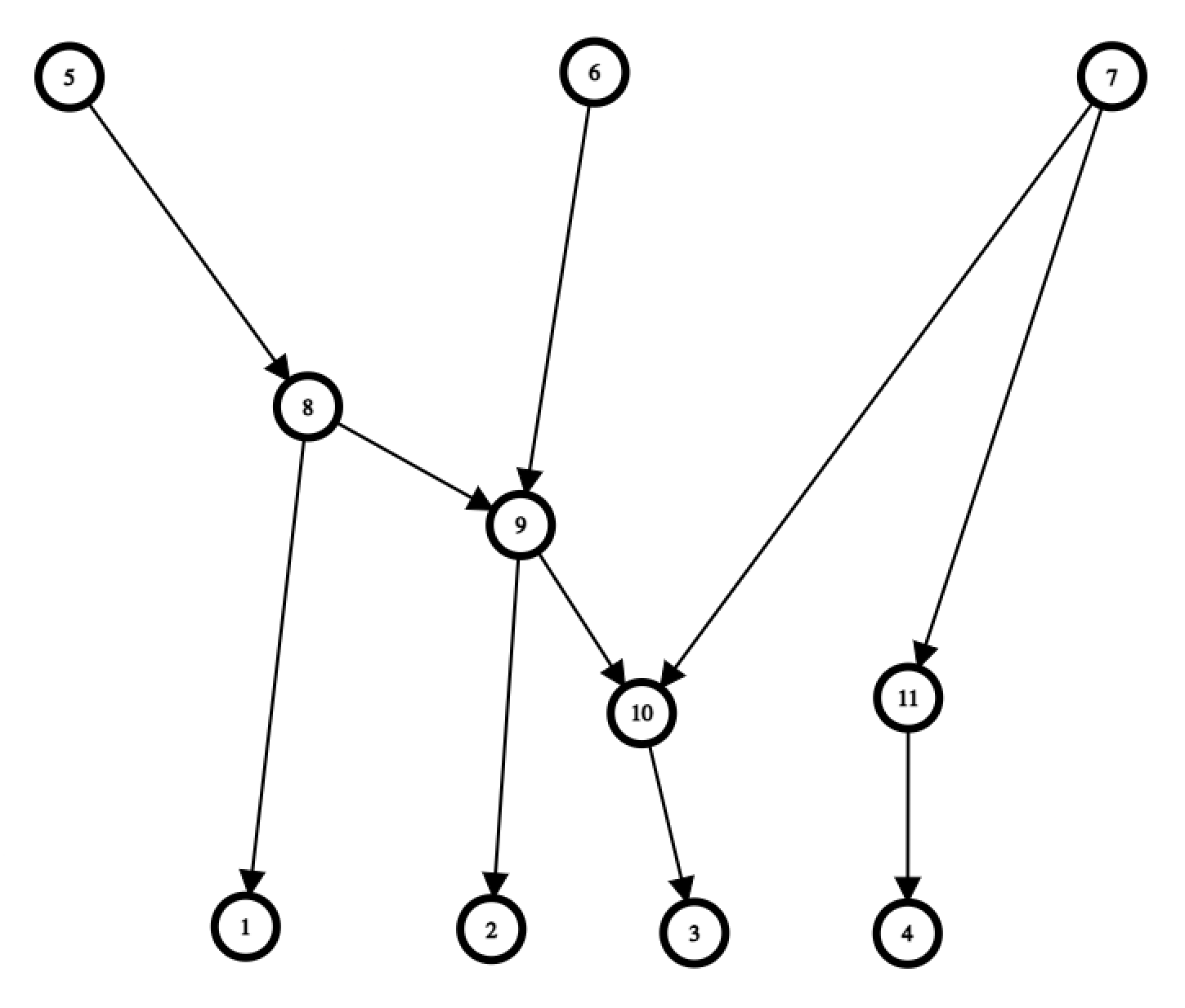
Vom incerca sa construim arborele astfel incat la pasul i+1, stim un subarbore format din primele i noduri si incercam sa adaugam nodul i+1 la acest subarbore:
Fie X un nod din primele i astfel incat, in arbore, nodul X este cel mai apropiat nod fata de i+1. In mod evident, acest nod este unic, si, pe drumul de la X la i+1 niciuna dintre muchii nu este cunoscuta, deci daca am stii care este acest nod X, am putea face un query de forma ? i+1 X pentru a lega nodul i+1 de nodul X fara riscul ca muchia stearsa sa fie una cunoscuta. Sa presupunem ca facem un query intre nodul i+1 si un nod aleator Y dintre primele i noduri, atunci, exista doua cazuri:

  1. muchia stearsa nu era o muchie cunoscuta, caz in care am adaugat nodul i+1 la subarborele cunoscut deci putem trece mai departe
  2. muchia stearsa era una cunoscuta. In acest caz, stim cu siguranta ca aceasta muchie se afla pe drumul de la Y la i+1 si, fiind o muchie cunoscuta, putem conclude ca aceasta muchie se afla pe drumul de la Y la X, ceea ce indica faptul ca nodul X se afla in subarborele de sub muchia stearsa, daca am presupune arborele ca avand radacina in Y, sau, cu alte cuvinte, nodul X se afla in directia indicata din nodul Y catre muchia stearsa. Cu aceasta informatie, observam ca subarborele pe care il cunosteam inainte s-a spart in alti doi subarbori: unul legat de nodul i+1 si altul care contine nodul X cautat. Deci acum putem face un alt query cu nodul i+1 si un nod aleator din subarborele care stim ca il contine pe X. Procedeul va fi analog, iar dupa acest query vom ramane tot cu un subarbore (pe care il cunoastem) care contine nodul i+1 si un alt subarbore care contine nodul X (subarbore pe care il cunoastem, dar in care nu stim care este nodul X). Astfel, putem continua sa facem query-uri pana cand una din muchiile sterse nu este una cunoscuta, caz in care ambii subarbori se vor uni si vom cunoaste unul de marime i+1. luati un exemplu daca nu e prea clar

Acest algoritm, implementat asa, desi are complexitate N*(N-1)/2 worst-case, in practica se comporta foarte bine chiar si pe interactorul adaptiv, si primeste aproximativ 65 de puncte.
Optimizarea care duce la un worst-case de aproximativ Nlog query-uri este observatia ca atunci cand alegem nodul Y cu care sa facem query, il putem alege in centroidul subarborelui in care il cautam pe X, astfel garantam ca il vom gasi pe X in maxim log pasi si deci il vom uni pe i+1 la subarborele cunoscut in maxim log pasi.
Numarul maxim de query-uri egal cu 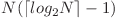N(\lceil log_2{N} \rceil - 1) este dat de faptul ca \sum_{i=1}^{N} \lceil log_2{i} \rceil = N\lceil log_2{N} \rceil - 2^{\lceil log_2{N} \rceil} + 1.
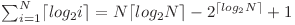Chiar daca numarul de query-uri pare foarte strict, in practica solutia abia face jumatate din acest upper_bound. sus
P.S. 4 din cele 5 sol explicate aici (fara cea de 10 puncte) sunt in sursa trimisa de pe summer21