Solutia problemei Portale

Solutie cu N*(N-1)/2 query-uri:

Intr-o matrice de adiacenta initial marcam toate muchiile ca muchie necunoscuta.
Trecem prin toate cele N*(N-1)/2 muchii posibile si pentru fiecare dintre ele, facem un query, marcam muchia curenta ca muchie care sigur se afla in arbore si, in cazul in care muchia stearsa era o muchie care sigur se afla in arbore, o marcam ca muchie care sigur nu se afla in arbore. btw. exista un easter egg in enuntul problemei portale
In final, cu acest algoritm vom cunoaste toate cele N-1 muchii intrucat dupa ce am facut i query-uri, vom stii despre fiecare dintre primele i muchii daca se afla sau nu in arbore
Aceasta implementare primeste aproximativ 10 puncte, dar poate fi optimizata foarte usor in doua modalitati:

  1. Ne oprim dupa ce stim ca dintre primele i muchii folosite in query-uri, N-1 sunt marcate ca muchie care sigur se afla in arbore - Cu aceasta optimizare, algoritmul merge foarte bine pe subtask-ul cu interactor random, si de aceea primeste aproximativ 35 de puncte.
  2. O alta observatie este faptul ca in momentul in care urmeaza sa facem query cu o muchie intre x si y, daca aceste doua noduri se afla in aceeasi componenta considerand muchiile marcate ca muchie care sigur se afla in arbore atunci putem spune ca muchia intre x si y este o muchie care sigur nu se afla in arbore, si nu mai este necesar sa facem acest query - Cu ambele optimizari, solutia primeste aproximativ 45 de puncte. amogus

Ideea pentru Nlog query-uri:

Vom incerca sa construim arborele astfel incat la pasul i+1, stim un subarbore format din primele i noduri si incercam sa adaugam nodul i+1 la acest subarbore:
Fie X un nod din primele i astfel incat, in arbore, nodul X este cel mai apropiat nod fata de i+1. In mod evident, acest nod este unic, si, pe drumul de la X la i+1 niciuna dintre muchii nu este cunoscuta, deci daca am stii care este acest nod X, am putea face un query de forma ? i+1 X pentru a lega nodul i+1 de nodul X fara riscul ca muchia stearsa sa fie una cunoscuta. Sa presupunem ca facem un query intre nodul i+1 si un nod aleator Y dintre primele i noduri, atunci, exista doua cazuri:

  1. muchia stearsa nu era o muchie cunoscuta, caz in care am adaugat nodul i+1 la subarborele cunoscut deci putem trece mai departe
  2. muchia stearsa era una cunoscuta. In acest caz, stim cu siguranta ca aceasta muchie se afla pe drumul de la Y la i+1 si, fiind o muchie cunoscuta, putem conclude ca aceasta muchie se afla pe drumul de la Y la X, ceea ce indica faptul ca nodul X se afla in subarborele de sub muchia stearsa, daca am presupune arborele ca avand radacina in Y, sau, cu alte cuvinte, nodul X se afla in directia indicata din nodul Y catre muchia stearsa. Cu aceasta informatie, observam ca subarborele pe care il cunosteam inainte s-a spart in alti doi subarbori: unul legat de nodul i+1 si altul care contine nodul X cautat. Deci acum putem face un alt query cu nodul i+1 si un nod aleator din subarborele care stim ca il contine pe X. Procedeul va fi analog, iar dupa acest query vom ramane tot cu un subarbore (pe care il cunoastem) care contine nodul i+1 si un alt subarbore care contine nodul X (subarbore pe care il cunoastem, dar in care nu stim care este nodul X). Astfel, putem continua sa facem query-uri pana cand una din muchiile sterse nu este una cunoscuta, caz in care ambii subarbori se vor uni si vom cunoaste unul de marime i+1. luati un exemplu daca nu e prea clar

Acest algoritm, implementat asa, desi are complexitate N*(N-1)/2 worst-case, in practica se comporta foarte bine chiar si pe interactorul adaptiv, si primeste aproximativ 65 de puncte.
Optimizarea care duce la un worst-case de aproximativ Nlog query-uri este observatia ca atunci cand alegem nodul Y cu care sa facem query, il putem alege in centroidul subarborelui in care il cautam pe X, astfel garantam ca il vom gasi pe X in maxim log pasi si deci il vom uni pe i+1 la subarborele cunoscut in maxim log pasi.
Numarul maxim de query-uri egal cu 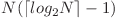N(\lceil log_2{N} \rceil - 1) este dat de faptul ca \sum_{i=1}^{N} \lceil log_2{i} \rceil = N\lceil log_2{N} \rceil - 2^{\lceil log_2{N} \rceil} + 1.
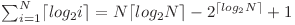Chiar daca numarul de query-uri pare foarte strict, in practica solutia abia face jumatate din acest upper_bound. sus
P.S. 4 din cele 5 sol explicate aici (fara cea de 10 puncte) sunt in sursa trimisa de pe summer21