Solutia problemei Transform3

Soluţia cu 2N + 2QlogN muchii

Peste şirul iniţial de lungime N generăm un arbore de intervale. Nodurile interne vor avea valori începând de la N+Q+1 (pentru că nodurile de la N+1 la N+Q sunt rezervate pentru rezolvarea restricţiilor problemei). Pentru N = 10 şi Q = 5, un exemplu de arbore de intervale este:

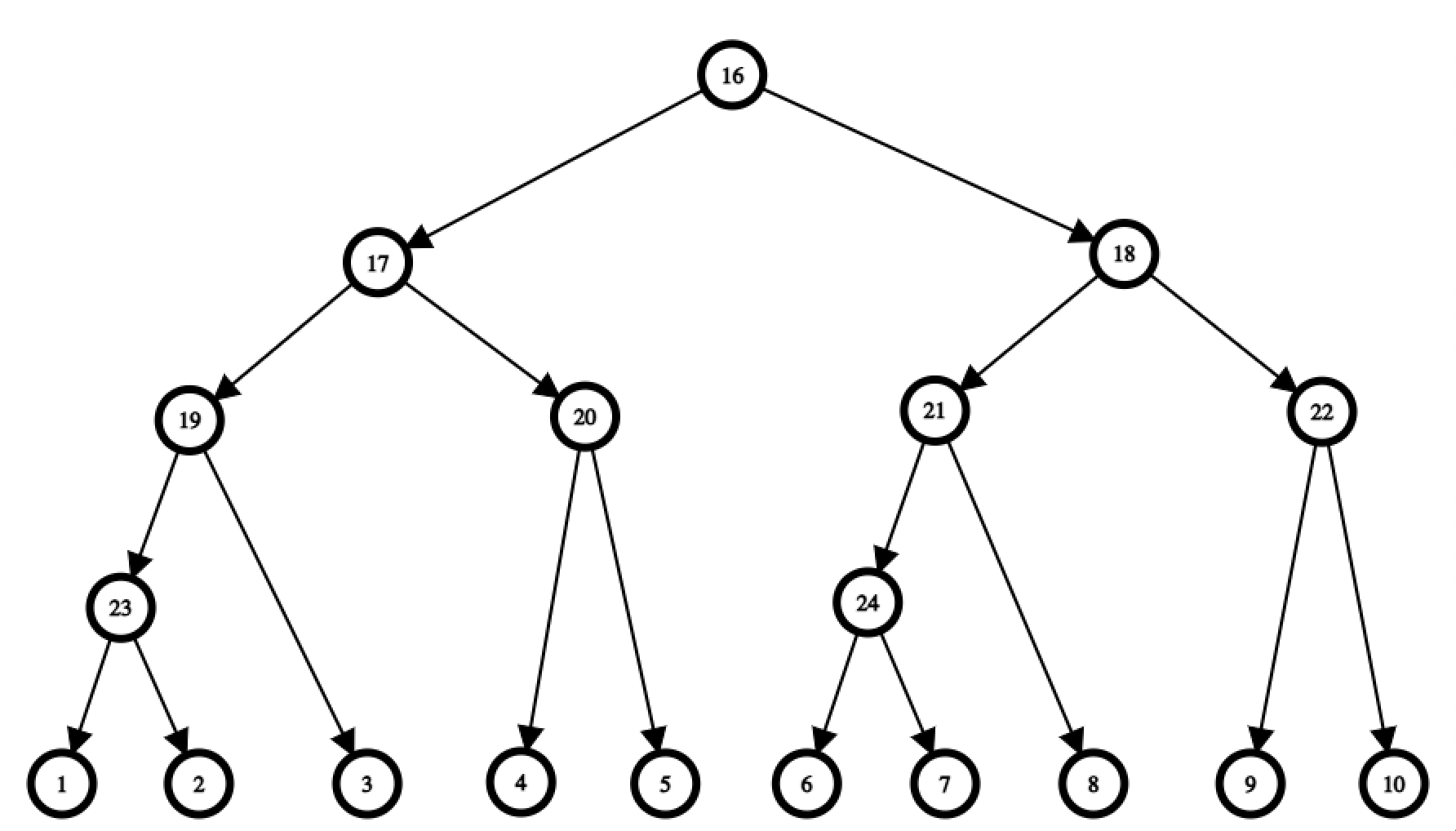
Până acum am folosit 2N muchii (deoarece un arbore de intervale construit peste un şir de lungime N are lungimea maxim 2N).

Pentru rezolvarea unei restricţii, putem să ne folosim de acest arbore de intervale astfel: ştim că orice interval 1 ≤ L ≤ R ≤ N poate fi acoperit cu maxim 2logN alte sub-intervale corespunzătoare unor noduri ale arborelui. Astfel, pentru fiecare restricţie, putem să tragem maxim 2logN muchii de la nodul corespunzător restricţiei (N+1 ≤ nod ≤ N+Q) la toate nodurile din arborele de intervale de care avem nevoie. De exemplu, dacă [L₁, R₁] = [2, 6] si [L₂, R₂] = [3, 9], vom trage următoarele muchii (restul restricţiilor au fost omise pentru claritate). În total vom folosi deci 2N + 2QlogN muchii.

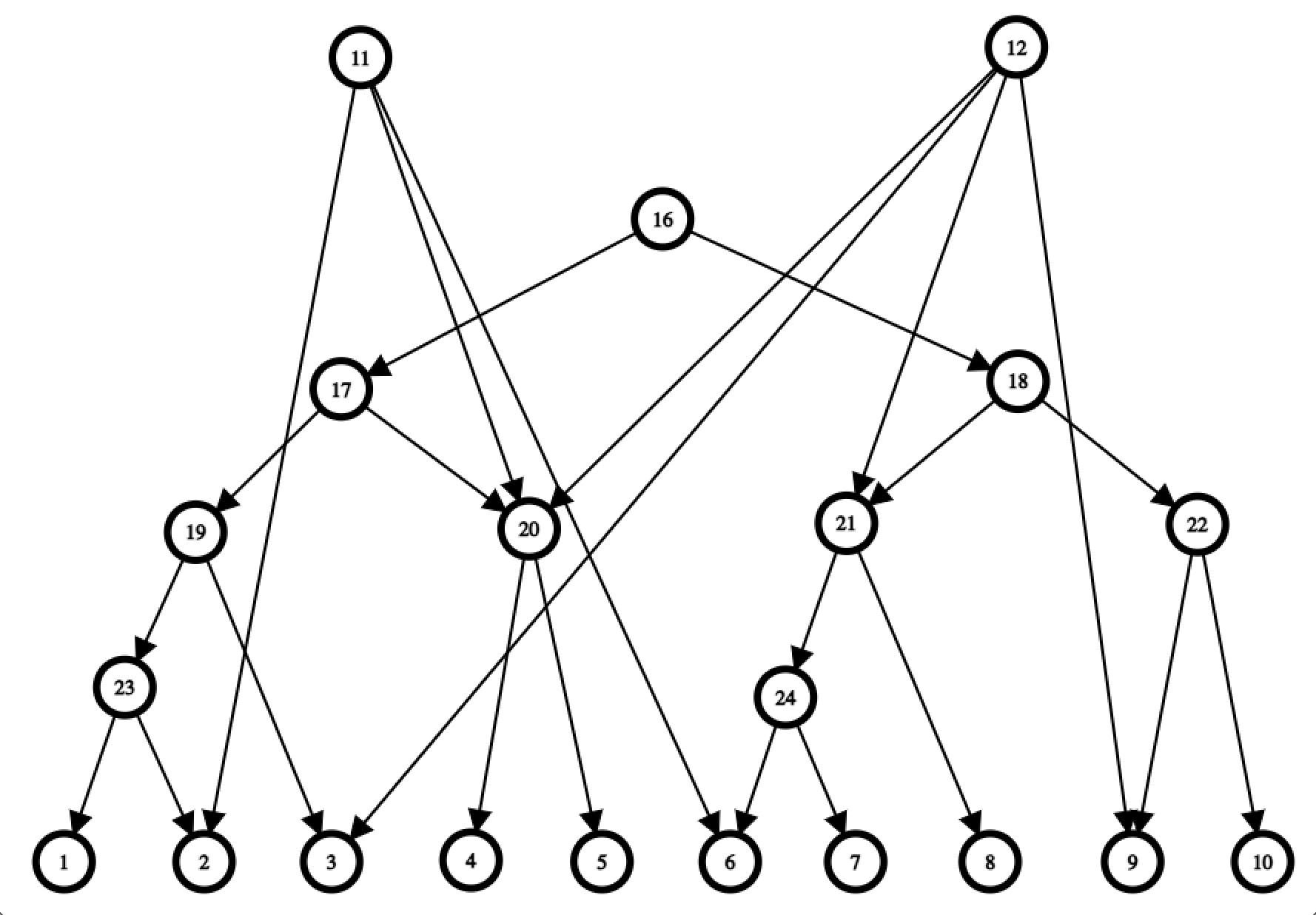
Soluţia cu 4N + 2Q muchii

Pentru a reduce numărul de muchii, trebuie să facem următoarele observaţii:

• Ideile bazate pe arbori duc în general la complexităţi "logaritmice" (apare un log prin complexitatea finală)
• Numărul de muchii cerut este 4N + 2Q care nu conţine niciun logaritm (deci este un hint că soluţiile bazate pe arbori nu duc la soluţia dorită)
• Nicăieri în soluţia precedentă nu ne folosim de proprietatea intervalelor din enunţ.
  Aşadar, în loc să plecăm de la un arbore, vom încerca să plecăm de la o structură "liniară", care în cazul nostru este o "coadă simulată cu 2 stive". Mai concret:

Fiecare interval din cele Q îl vom sparge în alte 2 sub-intervale (un prefix şi un sufix). Aceste 2 sub-intervale le vom retine folosind 2 stive puse una lângă alta. De exemplu o spargere pentru intervalul [4, 11] poate fi:

• leftStack: 6, 5, 4
• rightStack: 7, 8, 9, 10, 11.

Pentru fiecare din cele Q intervale date, vom încerca să le spargem în 2, folosindu-ne de informaţia de la intervalul precedent (acolo unde este posibil). Algoritmul simulat pentru intervalele [5, 10], [7, 12], [9, 13], [12, 14], [12, 15], [14, 17] este:

ID	Interval	leftStack	rightStack
1	[5, 10]	10, 9, 8, 7, 6, 5	-
2	[7, 12]	10, 9, 8, 7	11, 12
3	[9, 13]	10, 9	11, 12, 13
4	[12, 14]	14, 13, 12	-
5	[12, 15]	14, 13, 12	15

Modul de construcţie prezentat anterior este foarte asemănător cu modul în care este stocat std::deque în memorie şi este un şmen util în informatica de olimpiadă.

Mai departe, observăm că fiecărei stive la un moment dat îi corespunde un interval compact (de exemplu, stivei cu elementele {10, 9, 8, 7} îi corespunde intervalul [7, 10]) şi mai mult, unele intervale sunt incluse in altele (intervalul stivei {10, 9, 8, 7} este inclus în intervalul stivei {10, 9, 8, 7, 6, 5} sau intervalul stivei {11, 12} este inclus în intervalul stivei {11, 12, 13}).

Putem aşadar să atribuim fiecărei stive la un anumit moment de timp câte un interval (identificat printr-un cod unic mai mare strict decât N+Q) iar de la un interval oarecare putem să tragem muchie către cel mai mare interval inclus în interiorul sau (dacă există) şi câte o muchie la toate elementele neacoperite de acesta. În final, pentru fiecare restricţie, vom trage muchii de la nodul său corespunzător din intervalul [N+1, N+Q] la cele maxim 2 stive in care se va sparge intervalul.

Pentru exemplul din enunţ, algoritmul ar arăta cam aşa:

ID	Interval	leftStack	rightStack	cod leftStack	cod rightStack
1	[1, 3]	[1, 3]	-	8	-
2	[2, 3]	[2, 3]	-	9	-
3	[3, 4]	[3, 3]	[4, 4]	10	11

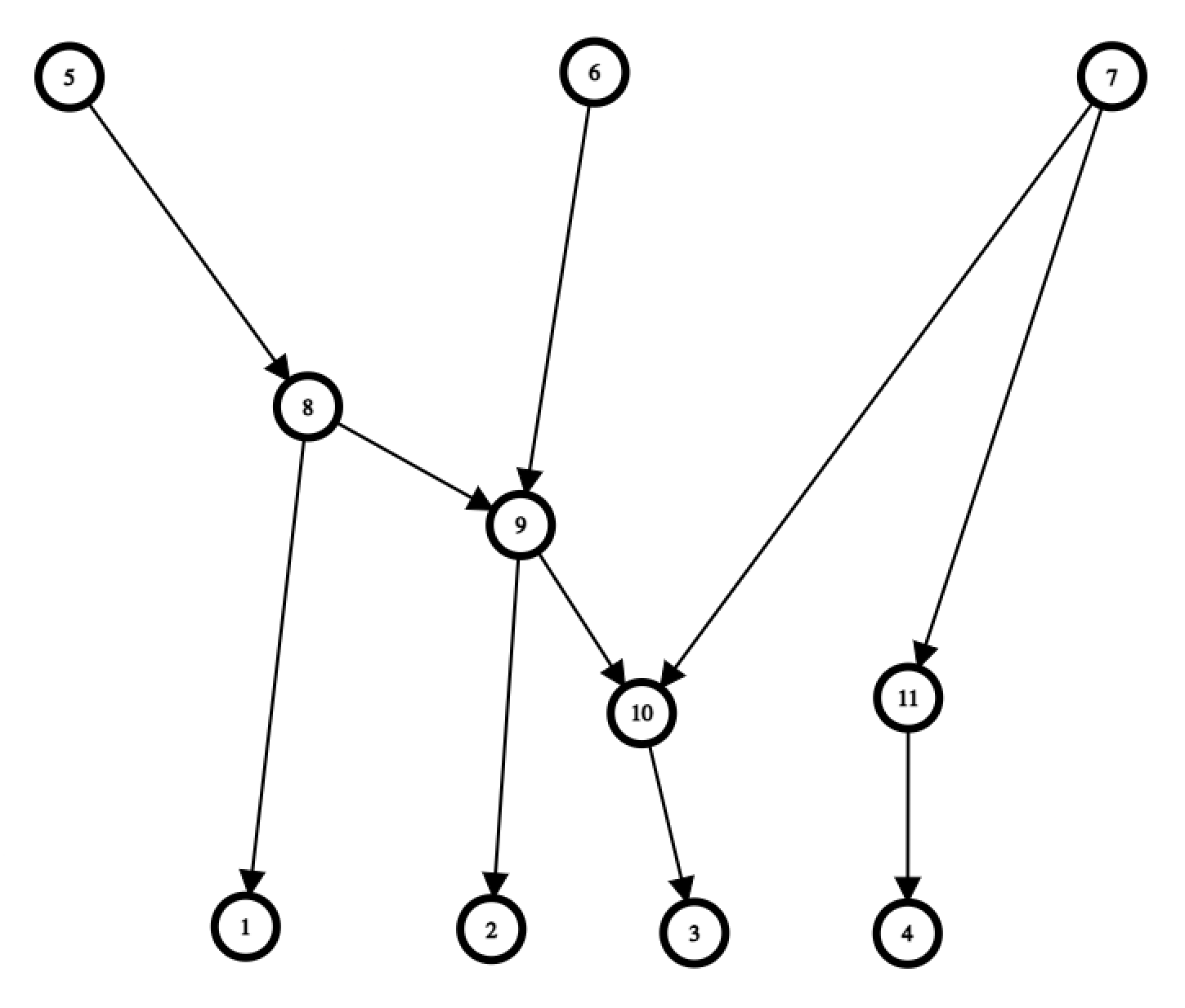
O ultimă observaţie este necesară pentru a obţine 100 de puncte: observăm ca leftStack[i] poate fi creat doar din leftStack[i + 1] (asta dacă la pasul i+1 intervalul nu este creat din nou), respectiv rightStack[i] poate fi creat din rightStack[i - 1] (dacă exista). Dacă atribuim la fiecare pas un cod unic fiecărei din cele 2 stive la un moment de timp, am obţine 2Q coduri distincte. În schimb, dacă atribuim coduri unice fiecărui interval distinct (cu alte cuvinte, nu atribuim coduri distincte dacă leftStack[i] = leftStack[i + 1] sau rightStack[i] = rightStack[i - 1]), atunci numărul de coduri atribuite se reduce la maxim 2N, maxim N pentru fiecare din cele 2 stive. Demonstraţia este următoarea (demonstrăm pentru leftStack, pentru rightStack se poate demonstra similar): leftStack[i] este fie construit din leftStack[i - 1] eliminând un prefix (schimbăm codul doar dacă acest prefix este nenul), fie reconstruită de la 0. Cum la fiecare pas, capătul stâng al intervalului asociat acestei stive creşte cu cel putin o poziţie, acesta fiind maxim N, numărul de coduri distincte asociate pentru toate stivele leftStack la toate momentele de timp este maxim N.