Revizia anterioară Revizia următoare
Siruri de sufixe
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
(Categoria Structuri de date, Autori Adrian Vladu, Cosmin Negruseri)
- Continut
- Introducere
- Ce sunt sirurile de sufixe (suffix arrays)?
- Cum construim un sir de sufixe?
- Calcularea celui mai lung prefix comun
(LCP) - Cautarea
- Probleme de concurs
- Concluzii
- Bibliografie
Introducere
Un domeniu important in algoritmica folosita in practica este acela al algoritmilor pe siruri de caractere. Astfel, la concursurile de programare sunt prezente foarte multe probleme de prelucrare si procesare a unor siruri de caractere. In cadrul concursurilor si antrenamentelor multi dintre noi s-au lovit de probleme ce s-ar fi rezolvat usor daca se reusea in mod eficient determinarea existentei unui cuvant ca subsecventa a unui alt cuvant. Vom prezenta o structura versatila ce permite acest lucru, inlesnind de multe ori realizarea altor operatii utile pe un string dat.
Ce sunt sirurile de sufixe (suffix arrays)?
Pentru a avea o idee mai buna despre suffix arrays, vom face inainte o scurta prezentare a structurii de date numita in engleza trie si a arborilor de sufixe (suffix trees[1]) care sunt o forma speciala a structurii de date trie. Un trie este un arbore menit sa stocheze siruri. Fiecare nod al lui va avea in general un numar de fii egal cu marimea alfabetului sirurilor de caractere care trebuies stocate. In cazul nostru, cu siruri ce contin litere mici ale alfabetului englez, fiecare nod va avea cel mult 26 de fii. Fiecare muchie porneste din tata spre fii si va fi etichetata cu o litera distincta a alfabetului. Etichetele legaturilor de pe un drum de la radacina pana la o frunza vor alcatui un cuvant stocat in arbore. Dupa cum se observa, verificarea existentei unui cuvant in aceasta structura de date este foarte eficienta si se realizeaza in complexitate O(M), unde M e lungimea cuvantului. Astfel, timpul de cautare nu depinde de numarul de cuvinte pe care trebuie sa il gestioneze structura de date, fapt ce face aceasta structura ideala pentru implementarea dictionarelor.
Sa vedem acum ce este un trie de sufixe. Dat fiind un string A = a0a1...an-1, notam cu Ai = aiai+1...an-1 sufixul lui A care incepe la pozitia i. Fie n = lungimea lui A. Trie-ul de sufixe este format prin comprimarea tuturor sufixelor A1...An-1 intr-un trie, ca in figura de mai jos. Trie-ul de sufixe corespunzator stringului abac este:
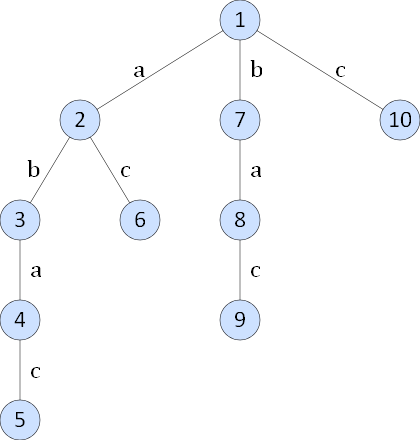
Operatiile pe aceasta structura se realizeaza extrem de usor:
- verificarea daca un string W este substring al lui A - este suficienta parcurgerea nodurilor, incepand din radacina si urmarind muchiile etichetate corespunzator caracterelor din W (complexitate O(|W|))
- cautarea celui mai lung prefix comun pentru doua sufixe ale lui A - se aleg nodurile u si v ale trie-ului corespunzatoare sfarsitului celor doua sufixe, iar prin aplicarea unui algoritm de gasire a LCA (Lowest Common Ancestor / cel mai apropiat stramos comun) se gaseste nodul corespunzator sfarsitului prefixului cautat. De exemplu, pentru abac si ac se gasesc nodurile 5 si 6. Cel mai apropiat stramos comun al lor este 2, de unde rezulta prefixul a. Autorii va recomanda articolul [2] pentru o rezolvare in O(sqrt(n)), [3] pentru o prezentare accesibila a unei rezolvari in O(log n) sau O(1), si articolul [4] pentru un algoritm "state of the art".
- gasirea celui de-al k-lea sufix in ordine lexicografica - (complexitate O(n), cu o preprocesare corespunzatoare). De exemplu al 3-lea sufix al sirului abac este reprezentat in trie-ul nostru de a 3-a frunza.
Desi ideea unui trie de sufixe este incantatoare la prima vedere, implementarea simplista in care inseram pas cu pas sufixele in structura noastra necesita un timp de ordinul O(n2). Exista o structura numita arbore de sufixe[1] care se poate construi in timp liniar fata de lungimea sirului de caractere. Arborele de sufixe este un trie de sufixe in care lanturile din care nu ieseau alte muchii erau comprimate intr-o singura muchie (in exemplul de mai sus acestea ar fi lanturile 2-3-4-5 si 1-7-8-9). Dar implementarea algoritmului de complexitate liniara pentru construirea unui arbore de sufixe este anevoioasa, fapt care ne determina sa cautam o alta structura, mai usor de realizat.
Sa vedem care sunt sufixele lui A, parcurgand arborele in adancime. Avand in vedere faptul ca la parcurgerea in adancime trebuie sa consideram nodurile in ordinea lexicografic crescatoare a muchiilor care le leaga de tata, obtinem urmatorul sir de sufixe:
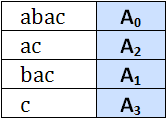
Este usor de observat ca acestea sunt ordonate crescator. Pentru memorare, nu este necesar sa pastram un vector ordonat de sufixe, suficienta fiind pastrarea indicilor fiecarui sufix din sirul ordonat. Pentru exemplul de mai sus obtinem vectorul P = (0, 2, 1, 3), acesta fiind array-ul de sufixe pentru stringul abac.
Cum construim un sir de sufixe?
Prima metoda care ne vine in minte este sortarea tuturor sufixelor lui A folosind un algoritm de complexitate O(n lg n). Insa compararea a doua sufixe se face in timp O(n), deci complexitatea finala va fi O(n2 lg n). Exista totusi un algoritm relativ usor de implementat si inteles, avand o complexitate de O(n lg n). Desi este asimptotic mai mare decat cel al constructiei unui arbore de sufixe (suffix tree), in practica timpul de constructie al unui sir de sufixe este mult mai mic, din cauza constantei care apare in fata algoritmul liniar. De asemenea, cantitatea de memorie folosita in cazul implementarii cu memorie O(n) este de la 3 pana la 5 ori mai mica decat in cazul unui arbore de sufixe.
Algoritmul se bazeaza pe mentinerea ordinii sufixelor sirului, sortate dupa prefixele lor de lungime 2k. Astfel vom executa m = [log2n] (marginit superior) pasi, la pasul k stabilind ordinea sufixelor daca sunt luate in considerare doar primele 2k caractere din fiecare sufix. Se foloseste o matrice P de dimensiune m x n. Notam cu Aik subsecventa lui A de lungime 2k ce incepe pe pozitia i. Pozitia lui Aik in sirul sortat al subsecventelor Ajk (j=0,n-1) se pastreaza in P(k,i).
Pentru a trece de la pasul k la pasul k+1 se concateneaza toate secventele Aik cu Ai+2k k, obtinandu-se astfel substringurile de lungime 2k+1. Pentru stabilirea ordinii se folosesc informatiile obtinute la pasul anterior. Pentru fiecare indice i se pastreaza o pereche de intregi formata din P(k,i) si P(k,i+2k). Nu trebuie sa ne preocupe faptul ca i+2k poate pica in afara sirului, deoarece vom completa sirul cu pseudocaracterul $, despre care vom considera ca este lexicografic mai mic decat oricare alt caracter. In urma sortarii, perechile vor fi aranjate conform ordinii lexicografice a substringurilor de lungime 2k+1 corespunzatoare. Un ultim lucru care mai trebuie notat este ca la un anumit pas k, pot exista doua (sau mai multe) substringuri Aik = Ajk, iar acestea trebuie etichetate identic (P(k,i) trebuie sa fie egal cu P(k,j)). O imagine spune mai mult decat o mie de cuvinte:

Pasul 0:
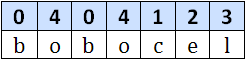
Pasul 1:
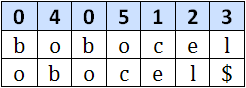
Pasul 2:
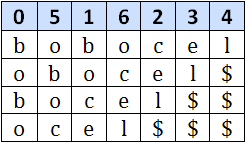
Pasul 3:
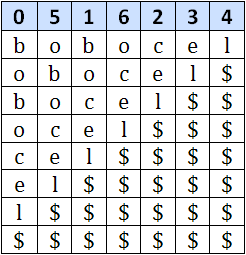
Iata un pseudocod ce sugereaza pasii principali ce trebuie urmati:
n <- lungime(A)
pentru i <- 0, n-1
P(0, i) <- pozitia lui Ai in sirul ordonat al caracterelor lui A
sfarsit pentru
cnt <- 1
pentru k <- 1, [log2 n] (marginit superior)
pentru i <- 0, n-1
L(i) <- (P(k-1, i), P(k-1, i+cnt), i)
sfarsit pentru
sorteaza L
calculeaza P(k, i), i = 0, n-1
cnt <- 2 * cnt
sfarsit pentruDe remarcat ca nu este neaparat necesara o anumita numerotare a substringurilor, atat timp cat intre ele este pastrata o relatie de ordine valida. In vederea atingerii complexitatii O(n lg n) pentru sortare se recomanda folosirea metodei radix sort (de doua ori sortare prin numarare), aceasta avand complexitate O(n). Insa, pentru usurarea implementarii, se poate folosi functia sort() din STL (Standard Template Library, o librarie ce contine unele structuri de date si algoritmi in limbajul C++). Desi complexitatea va creste la O(n lg2 n) in cazul cel mai defavorabil, implementarea devine simtitor mai simpla, iar in practica diferentele sunt abia sesizabile pentru siruri cu lungime mai mica decat 100 000.
Mai jos puteti vedea o implementare extrem de scurta pentru suffix array in O(n lg2 n).
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 65536;
const int MAXLG = 17;
char A[MAXN];
struct entry {
int nr[2], p;
} L[MAXN];
int P[MAXLG][MAXN], N, i, stp, cnt;
bool cmp(const entry &a, const entry &b) {
return a.nr[0] == b.nr[0] ? (a.nr[1] < b.nr[1]) : (a.nr[0] < b.nr[0]);
}
int main() {
gets(A);
for (N = strlen(A), i = 0; i < N; ++i)
P[0][i] = A[i] - 'a';
for (stp = 1, cnt = 1; cnt >> 1 < N; ++stp, cnt <<= 1) {
for (i = 0; i < N; ++i) {
L[i].nr[0] = P[stp - 1][i];
L[i].nr[1] = i + cnt < N ? P[stp - 1][i + cnt] : -1;
L[i].p = i;
}
sort(L, L + N, cmp);
for (i = 0; i < N; ++i)
P[stp][L[i].p] = i > 0 && L[i].nr[0] == L[i - 1].nr[0] && L[i].nr[1] == L[i - 1].nr[1] ? P[stp][L[i - 1].p] : i;
}
return 0;
}Sirul de sufixe se va gasi pe ultima linie a matricei P. Cautarea celui de-al k-lea sufix in ordine lexicografica este acum imediata, deci nu vom reveni asupra acestui aspect.
Cantitatea de memorie folosita poate fi redusa renuntand la folosirea intregii matrice P si pastrindu-se la fiecare pas doar ultimele doua linii ale acesteia. In acest caz, insa, structura nu va mai fi capabila sa execute eficient operatia ce urmeaza.
Calcularea celui mai lung prefix comun (LCP)
Se dau doua sufixe ale unui string A. Se cere calcularea celui mai lung prefix comun al lor. Am aratat ca un arbore de sufixe poate realiza aceasta in timp O(1) cu o preprocesare corespunzatoare. Sa vedem daca un sir de sufixe poate atinge aceeasi performanta.
Fie cele doua sufixe Ai si Aj. Folosind matricea P, putem itera descrescator de la cel mai mare k pana la 0 si verifica daca Aik = Ajk. Daca cele doua prefixe sunt egale, am gasit un prefix comun de lungime 2k. Nu ne ramane decat sa actualizam i si j, incrementandu-le cu 2k si sa verificam in continuare daca mai gasim prefixe comune. Codul functiei care calculeaza LCP este foarte simplu:
int lcp(int x, int y) {
int k, ret = 0;
if (x == y) return N - x;
for (k = stp - 1; k >= 0 && x < N && y < N; --k)
if (P[k][x] == P[k][y])
x += 1 << k, y += 1 << k, ret += 1 << k;
return ret;
}Complexitatea este insa O(lg n) pentru un calcul al acestui prefix. Reducerea la O(1) se bazeaza pe urmatoarea observatie: lcp(x, y) = min{ lcp(x, x + 1), lcp(x + 1, x + 2), ..., lcp(y - 1, y) }. Demonstratia este imediata daca ne uitam in arborele de sufixe corespunzator. Asadar, este suficient ca la inceput sa calculam cel mai lung prefix comun intre toate perechile de sufixe consecutive (timp O(n lg n)) si sa introducem o structura aditionala ce permite calculul in O(1) al minimului dintr-un interval. Cea mai eficienta astfel de structura este cea pentru RMQ (range minimum query), despre care nu vom da detalii aici, dar care este studiata in amanunt in [3], [4] si [5]. Cu inca o preprocesare in O(n lg n) ceruta de noua structura putem acum sa raspundem in O(1) query-urilor LCP. Structura folosita de RMQ cere tot O(n lg n) memorie, asadar timpul si memoria finale necesare sunt O(n lg n).
Cautarea
Deoarece sirul de sufixe ne ofera ordinea sufixelor lui A, cautarea unui string W in A se poate face simplu cu o cautare binara. Deoarece compararea se face in O(|W|), cautarea va avea complexitatea O(|W| lg n). Lucrarea [6] ofera structurii de date si algoritmului de cautare cateva rafinamente ce permit reducerea timpului la O(|W| + lg n), dar autorii nu considera ca acestea sunt folositoare in concursurile de programare.
Probleme de concurs
Autorii au incercat sa adune cat mai multe probleme ce pot fi rezolvate cu ajutorul sirurilor de sufixe. Parcurgerea tuturor problemelor la prima citire, ar putea fi greoaie pentru un cititor care a avut primul contact cu aceasta structura de date citind acest articol. Pentru a usura lectura problemele sunt asezate intr-o ordine crescatoare a dificultatilor.
Problema 1: Parola ascunsa (acm 2003, enunt modificat)
Consideram un sir de caractere de lungime n (1 ≤ n ≤ 100000). Sa se determine rotatia lui circulara lexicografic minima. De exemplu, rotatiile sirului de caractere alabala sunt:
alabala
labalaa
abalaal
balaala
alaalab
laalaba
aalabal
iar cea mai mica dintre ele in ordine lexicografica este aalabal.
Solutie:
De obicei, in probleme unde apare rotatia unui sir dat, putem sa ne folosim de trucul de a concatena sirului de caractere acelasi sir pentru a simplifica problema. Dupa aceasta transformare problema ne cere subsecventa lexicografica minima de lungime n a noului sir. Ordinea subsecventelor de lungime n ale unui sir este egala cu ordinea sufixelor determinate de subsecventele date, deci ne putem folosi de siruri de sufixe pentru a rezolva aceasta problema.
O problema asemanatoare a fost propusa de unul dintre autori la concursul Bursele Agora, editia 2003-2004, care se putea rezolva pe aceiasi idee. Implementarea trebuia facuta atent pentru solutia oficiala era o rezolvare eficienta ce nu folosea aceasta structura de date.
Problema 2: Sir (baraj 2004)
Se considera un sir c1c2...cn format din n (1 ≤ n ≤ 30 000) caractere din multimea {A, B}. Concatenam sirul cu el insusi si obtinem un sir de lungime 2n. Pentru un indice k (1 ≤ k ≤ 2n) consideram subsecventele de lungime cel mult n, care se termina pe pozitia k, iar dintre acestea fie s(k) subsecventa cea mai mica in ordine lexicografica. Determinati indicele k pentru care s(k) are lungimea cea mai mare.
Nota suplimentara: fie X si Y doua siruri oarecare, iar "o" operatia de concatenare. In aceasta problema se va considera ca X > X o Y.
Solutie:
Sirul cautat este prima permutare circulara in ordine lexicografica a sirului dat. Notam cu Sik substringul de lungime k ce incepe la pozitia i. Fie Sin cel mai mic substring in ordine lexicografica de lungime n al sirului obtinut prin concatenare. Presupunand prin absurd ca s(i+n-1) < n ar insemna ca exista un i' (i < i' ≤ j) astfel incat Si'j-i'+1 este lexicografic mai mic decat Sin. Dar din conditia impusa de enunt avem Si'j-i'+1 > Si'n. Dar Si'n > Sin => contradictie.
Desi exista un algorirm de complexitate O(n) specializat pentru siruri ce contin doar literele A si B, metoda preferata de autor (si cu care a obtinut punctaj maxim in timpul concursului) a fost folosirea sirurilor de sufixe, ca in problema anterioara.
Problema 3: Substr (baraj 2003)
Se da un text format din N caractere (litere mari, litere mici si cifre). Un substring al acestui text este o secventa de caractere care apar pe pozitii consecutive in text. Fiind dat un numar K, sa se gaseasca lungimea celui mai lung substring care apare in text de cel putin K ori (1 ≤ N ≤ 16384).
Solutie:
Avand sufixele textului sortate, iteram cu o variabila i de la 0 la N-K si calculam cel mai lung prefix comun intre sufixul i si sufixul i+K-1. Prefixul maxim determinat in cursul acestei parcurgeri reprezinta solutia problemei.
Problema 4: Ghicit (baraj 2003)
Tu si cu Taranul jucati un joc neinteresant. Tu ai un sir de caractere mare. Taranul iti spune un alt sir de caractere, iar tu trebuie sa raspunzi cat mai repede daca sirul respectiv este sau nu o subsecventa a sirului tau.
Taranul iti pune multe intrebari si, fiindca esti informatician, te-ai gandit ca ar merge mai repede daca ai sti dinainte toate sirurile despre care te poate intreba.
Inainte de a face toata acesta munca te-ar interesa numarul total de subsecvente distincte ale sirului tau, ca sa stii daca are sens sa te apuci de acesta treaba sau nu.
Scrieti un program care afla numarul de subsecvente distincte ale unui sir de caractere dat. (1 ≤ lungimea sirului ≤ 10 000)
Solutie:
Aceasta problema ne cere, de fapt, sa calculam numarul de noduri (fara radacina) ale trie-ului de sufixe asociat unui string. Fiecare secventa distincta din sir este determinata de drumul unic pe care il parcurgem in trie-ul de sufixe cand cautam acea secventa. Pentru exemplul abac avem secventele a, ab, aba, abac, ac, b, ba, bac si c, acestea sunt determinate de drumul de la radacina trieului spre nodurile 2, 3, 4, 5, 6, 7, 8 si 9 in aceasta ordine. Cum constructia trie-ului de sufixe are complexitate patratica, iar construirea unui arbore de sufixe este anevoioasa, este preferabila o abordare prin prisma sirurilor de sufixe. Obtinem sirul sortat de sufixe in O(n lg n), dupa care cautam pozitia in care fiecare pereche de sufixe consecutive difera (folosind functia lcp) si adunam la solutie restul caracterelor. Complexitatea totala este O(n lg n).
Problema 5: SETI (ONI 2002, enunt modificat)
Se da un string de lungime N (1 ≤ N ≤ 131072) si M stringuri de lungime cel mult 64. Se cere sa se numere aparitiile fiecarui string din cele M in stringul mare.
Solutie:
Se procedeaza la fel ca in cazul sirurilor de sufixe, numai ca este suficient sa ne oprim dupa pasul 6, unde am calculat relatia de ordine intre stringurile de lungime 26 = 64. Avand substringurile de lungime 64 sortate, fiecare query este rezolvat cu doua cautari binare. Complexitatea algoritmului este O(N lg 64 + M * 64 * lg N) = O(N + M lg N).
Problema 6: Subsecventa comuna (Olimpiada poloneza si TopCoder 2004, enunt modificat)
Se considera trei siruri de caractere S1, S2 si S3, de lungimi m, n si p (1 ≤ m, n, p ≤ 10000). Sa se determine subsecventa de lungime maxima care este comuna celor trei siruri. De exemplu, daca S1 = abababca, S2 = aababc si S3 = aaababca, atunci subsecventa comuna de lungime maxima pentru cele trei siruri este ababc.
Solutie:
Daca ar fi vorba doar de doua siruri de lungimi mai mici am putea rezolva usor problema folosind metoda programarii dinamice; astfel, solutia pentru doua siruri ar avea ordinul de complexitate O(N2).
O alta idee ar fi sa consideram fiecare sufix al sirului S1 si sa incercam sa ii gasim potrivirea de lungime maxima in celelalte doua siruri.
Potrivirea de lungime maxima rezolvata naiv ar avea complexitatea O(N2), dar folosind algoritmul KMP[8], putem obtine prefixul maxim al unui sir care se gaseste ca subsecventa in al doilea sir in O(N), iar utilizand aceasta metoda pentru fiecare sufix al lui S1, am avea o solutie al carei ordin de complexitate este O(N2).
Sa vedem ce se intampla daca sortam sufixele celor trei siruri:

Acum interclasam prefixele celor trei siruri (consideram § < # < @ < a ...):

Subsecventa comuna maxima corespunde prefixelor comune maxime pentru cele trei sufixe ababca§, ababc# si ababca@. Urmariti unde apar ele in sirul sortat al tuturor sufixelor. De aici avem ideea ca solutia se afla ca o secventa [i..j] a sirului sortat de sufixe cu proprietatea ca secventa contine cel putin cate un sufix din fiecare sir, iar prefixul cel mai lung comun primului sufix din secventa si ultimul sufix din secventa este maxim; acest cel mai lung prefix este chiar solutia problemei. Alte subsecvente comune ale celor trei siruri ar fi prefixe comune pentru cate o subsecventa a sirului de sufixe sortat, de exemplu bab pentru bababca§, babc@, babca§, sau a pentru a§, a@, aaababca@, aababc#. Pentru a determina aceasta secventa de prefix comun maxim putem folosi o parcurgere cu doi indici (start si end). Indicele start variaza intre 1 si numarul de sufixe, iar end este cel mai mic indice mai mare decat start astfel incat intre start si end sa existe sufixe din toate cele trei siruri. Astfel, perechea [start, end] va indica, la un moment dat, secventa optima [i..j]. Aceasta parcurgere este liniara, deoarece start poate avea cel mult n valori, iar end va fi incrementat de cel mult n ori. Pentru a sorta sirul tuturor sufixelor nu este nevoie sa sortam mai intai sufixele fiecarui sir si apoi sa interclasam sufixele. Putem realiza operatia mult mai simplu concatenand cele trei siruri in unul singur (pentru exemplul considerat avem abababca§aababc@aaababca#) si sortand sufixele acestuia.
Problema 7: Cel mai lung palindrom (USACO Training Gate)
Se considera un sir de caractere S de lungime n (1 ≤ n ≤ 20000). Determinati subsecventa de lungime maxima care este si palindrom (un sir de caractere este palindrom daca este identic cu sirul obtinut prin oglindirea sa).
Solutie:
Daca dorim sa determinam, pentru un indice fixat i, care este cel mai mare palindrom centrat in i atunci ne intereseaza prefixul maxim al subsecventei S[i+1..n] care se potriveste cu prefixul subsecventei S[1..i] reflectate. Pentru a rezolva cu usurinta aceasta problema sortam impreuna si sufixele sirului cu prefixele reflectate ale sirului (operatie care se realizeaza usor concatenand sirul S§ cu sirul S oglindit, S') si vom efectua interogari pentru cel mai lung prefix comun pentru S[i+1] si S'[n-i+1] (S'[n-i+1] = S[1..i]), la care putem raspunde folosind siruri de sufixe in timp O(1). Astfel, putem rezolva problema in timp O(N log N). Sa observam ca am tratat aici doar cazul in care palindromul este de lungime para, dar cazul in care palindromul are lungime impara se trateaza analog.
Problema 8: Template (Olimpiada poloneza 2004, enunt modificat)
Pentru un string A, sa se determine lungimea minima a unui substring B cu proprietatea ca A poate fi obtinut prin lipirea intre ele a mai multor stringuri B (la lipire doua stringuri se pot suprapune, dar in locurile in care se suprapun caracterele celor doua stringuri trebuie sa coincida).
Exemplu
Pentru string-ul ababbababbabababbabababbababbaba rezultatul este 8. String-ul B de lungime minima este ababbaba. A poate fi obtinut din B astfel:
ababbababbabababbabababbababbaba
ababbaba
.....ababbaba
............ababbaba
...................ababbaba
........................ababbaba
Solutia 1:
O solutie simpla foloseste siruri de sufixe, un arbore echilibrat si un max-heap (se pot folosi structurile set si priority_queue din STL). Este evident ca sablonul cautat este un prefix al lui A. Asadar, pentru fiecare prefix B al lui A vom verifica daca prin lipirea tuturor aparitiilor lui B in A se obtine chiar cuvantul initial A. Pentru a face aceasta verificare este suficient calculul distantei dintre perechile de potriviri consecutive ale lui B. Trebuie sa avem grija ca prefixele sa acopere si sfarsitul sirului. Pentru aceasta, cel mai comod este sa mai consideram o aparitie a lui B pe pozitia n+1. Daca distanta maxima gasita este mai mare decat lungimea lui B, acel prefix nu reprezinta o solutie. Pentru o rezolvare eficienta, vom considera initial B ca fiind prefixul de lungime 1, urmand sa introducem la sfarsitul sau, caracter cu caracter, restul caracterelor string-ului A. Daca la fiecare pas mentinem multimea S a pozitiilor de inceput ale potrivirilor lui B in A, dupa introducerea unui nou caracter in B, multimea S va "pierde" anumite elemente (posibil niciunul). Pentru administrare eficienta, vom considera sirul sortat de sufixe ale lui A si doi pointeri, L si R, reprezentand primul, respectiv ultimul sufix din sir care il au ca prefix pe B. La adaugarea unui nou caracter in B, se incrementeaza, respectiv decrementeaza L si R cat timp acestea nu indica sufixe care il au ca prefix pe noul B. Arborele echilibrat va contine tot timpul pozitiile de inceput ale sufixelor continute intre L si R, iar heap-ul va contine distantele intre elemente consecutive ale arborelui. La inserarea unui nou caracter in B, trebuie sa avem grija de intretinerea acestor structuri. Algoritmul se incheie atunci cand cel mai mare (primul) element din heap este mai mic sau egal cu lungimea lui B. Lungimea finala a lui B ne ofera rezultatul cautat. Ordinul de complexitate este O(N lg N), unde N este lungimea lui A. Sa consideram un exemplu. S este marcat cu 1 in pozitiile in care s-a gasit o potrivire a lui B in A:
1: aab
2: aabaab
3: ab
4: abaab
5: abaabaab
6: b
7: baab
8: baabaab
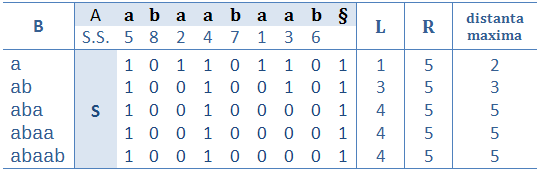
Solutia 2 (Mircea Pasoi):
Pentru sirul de caractere S, determinam pentru fiecare i de la 1 la n lungimea celui mai lung prefix al lui S cu S[i..n]. Aceasta operatie se poate realiza folosind siruri de sufixe. De exemplu, daca S este sirul nostru si T este sirul de potriviri maxime ale sufixelor, atunci:

Pentru toate lungimile posibile k ale sablonului (1 ≤ k ≤ n) verificam daca distanta maxima d intre indicii celor mai departate doua elemente de valori mai mari sau egale cu k in sirul T nu este mai mare decat k. Prezentam in continuare un exemplu:
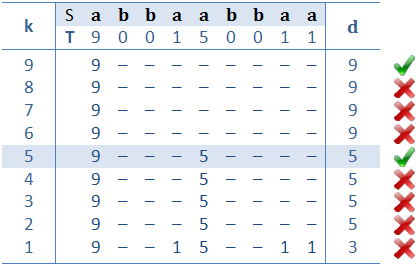
Cea mai mica valoare a lui k pentru care distanta d este suficient de mica reprezinta lungimea sablonului cautat (in cazul precedent k = 5). Pentru a obtine un algoritm de complexitate buna trebuie ca acest pas sa fie eficient; putem sa folosim un arbore de intervale, sa folosim un contor cu k care variaza de la 1 la n si sa eliminam din arbore elemente de marime mai mica decat k si, la fiecare pas, sa actualizam arborele pentru a putea raspunde la interogari de genul: care este distanta maxima intre doua elemente care exista acum in structura. Algoritmul are complexitatea O(N log N). Pentru o prezentare amanuntita a arborilor de intervale, va recomand [9] si [10].
Problema 9 (Olimpiada Baltica de Informatica[11], 2004)
Un sir de caractere S se numeste repetitie (K, L) daca S se obtine prin concatenarea de K ≥ 1 ori a unui sir T de lungime L ≥ 1. De exemplu, sirul S = abaabaabaaba este o repetitie (4, 3) cu T = aba. Sirul T are lungimea trei si S se obtine repetandu-l pe T de patru ori. Avand un sir de caractere U format din caractere a si/sau b de lungime n (1 ≤ n ≤ 50000), va trebui sa determinati o repetitie (K, L) care apare ca subsecventa a lui U astfel incat K sa fie cat mai mare. De exemplu, sirul U = babbabaabaabaabab contine repetitia (4, 3), sirul S incepand de pe pozitia 5. Aceasta este si repetitia maxima, deoarece sirul nu mai contine nici o alta subsecventa care sa se repete de mai mult de patru ori. Daca sirul contine mai multe solutii cu acelasi K, poate fi aleasa oricare dintre ele.
Solutie:
Dorim ca pentru un L fixat sa determinam cea mai mare valoare K astfel incat in sirul U sa avem o subsecventa S care este repetitie (K, L). Vom considera acum un exemplu: U = babaabaabaabaaab, L = 3 si o subsecventa fixata X = aab care incepe pe pozitia 4 a sirului U. Putem incerca sa extindem secventa aab la ambele capete cat mai mult posibil prin repetarea ei asa cum vedem in continuare:
b a b a a b a a b a a b a a a b
a a b a a b
a b a a b a a b a a b a a b a
Extinzand in acest mod cat mai mult in stanga secventa noastra si apoi extinzand la dreapta prefixul de lungime L (in exemplul nostru prefixul de lungime 3) al secventei obtinute, gasim cea mai lunga repetitie a unui sir de caractere de lungime L cu proprietatea ca repetitia contine ca subsecventa sirul X (daca repetitia este (1, L) afirmatia anterioara nu este adevarata, dar acesta este un caz trivial). Acum observam ca pentru a identifica toate repetitiile (K, L) cu L fixat din sirul U, este suficient sa partitionam sirul in n/L bucati si sa extindem aceste bucati. Remarcam ca daca va fi posibil sa realizam acest lucru pentru ficare bucata in O(1) algoritmul final va avea ordinul de complexitate O(n/1 + n/2 + n/3 + .. + n/n) (fiecare bucata se poate repeta in totalitate sau doar partial in stanga sau in dreapta, iar noi nu vom extinde fiecare bucata separat, ci bucatile adiacente le vom reuni intr-o noua bucata; asadar, daca avem p bucati consecutine de aceeasi dimensiune, vom determina extinderile lor maxime in timp O(p)). Dar stim ca sirul 1 + 1/2 + 1/3 + 1/4 + .. + 1/n - ln n converge spre o constanta c, numita constanta lui Euler, si c < 1; de aici tragem concluzia ca O(n/1 + n/2 + n/3 + .. + n/n) = O(n log n), deci algoritmul, in cazul in care extinderile maxime pot fi calculate usor, ar avea ordinul de complexitate O(n log n). Acum intervin in rezolvarea noastra arborii de sufixe. Pentru a determina cu cat putem extinde cel mai mult subsecventa U[i..j] a sirului U la dreapta, practic ne intereseaza cel mai lung prefix comun al subsecventei U[i..j] si al subsecventei U[j+1..n]. Pentru a extinde cat mai mult la stanga este suficient sa inversam sirul U si ajungem sa rezolvam aceeasi problema. Am vazut ca problema celui mai lung prefix comun a doua secvente se rezolva in timp O(1) cu ajutorul sirurilor de sufixe. Astfel, avem nevoie de crearea sirului de sufixe, etapa pe care o rezolvam intr-un timp de ordinul O(n log n) si apoi de aplicarea algoritmului explicat anterior care are complexitatea O(n log n). In concluzie, algoritmul prezent are complexitatea totala O(n log n).
Problema 10 (ACM SEER 2004)
Avand un sir de caractere S dat, se cere ca pentru fiecare prefix al sau sa se determine daca este un sir de caractere periodic. Astfel, pentru fiecare i (2 ≤ i ≤ N) ne intereseaza cel mai mare K ≥ 1 (daca exista un asemenea K) cu proprietatea ca prefixul lui S de lungime i poate fi scris cub forma Ak (sirul A concatenat cu el insusi de k ori) pentru un sir de caractere A. De asemenea, ne intereseaza si valoarea k (avem 0 ≤ N ≤ 1000000).
Exemplu
Pentru sirul aabaabaabaab obtinem rezultatul prezentat in continuare:
2 2
6 2
9 3
12 4
Explicatii
- prefixul aa are perioada a;
- prefixul aabaab are perioada aab;
- prefixul aabaabaab are perioada aab;
- prefixul aabaabaabaab are perioada aab;
Solutie:
Sa vedem ce se intampla cand incercam sa potrivim un sir cu un sufix al sau. Consideram un sir si il impartim in doua, obtinand un prefix si un sufix:
S = aab aabaabaaaab
suf = aab aabaaaab
pre = aab
Daca sufixul se potriveste cu sirul initial pe un numar de caractere mai mare sau egal cu lungimea sirului pre, inseamna ca pre este si un prefix al sufixului; deducem ca putem imparti si sufixul in pre si suf1, iar sirul putem sa il impartim in pre, pre si suf1. Daca sirul se potriveste cu sufixul pe un numar de caractere mai mare sau egal cu dublul lungimii sirului pre, atunci sufixul se potriveste cu suf1 pe un numar de caractere mai mare sau egal cu lungimea sirului pre, deci suf1 poate fi scris ca pre si suf2, deci suf poate fi scris ca pre, pre, suf2, iar S poate fi scris ca pre, pre, pre, suf2:
S = aab aab aab aaaab
suf = aab aab aaaab
suf1 = aab aaaab
pre = aab
Observam astfel ca daca sirul S se potriveste cu sufixul sau pe cel putin k * |pre| caractere, atunci S are un prefix de lungime (k+1) * |pre| care este periodic. Folosindu-ne de structura de date siruri de sufixe, putem determina pentru fiecare sufix potrivirea maxima cu sirul initial. Daca al i-lea sufix se potiveste cu sirul pe primele k * (i-1) pozitii, atunci putem actualiza informatia care indica daca prefixele de dimensiune j * (i-1) (unde 2 ≤ j ≤ k) sunt periodice. Pentru fiecare sufix S, actualizarea tuturor informatiilor are ordinul de complexitate O(n / (i-1)). Astfel, ordinul de complexitate al algoritmului de rezolvare a acestei probleme este O(n log n). Trebuie remarcat faptul ca putem obtine o rezolvare in timp O(n) folosind o idee similara si algoritmul KMP, dar prezentarea acestei rezolvari depaseste scopul acestui articol.
Concluzii
Mentionam ca in timpul concursurilor autorii prefera solutiile ale caror ordine de complexitate sunt O(n log2 n), mai lente, dar mai usor de implementat, si care folosesc un spatiu de memorie de ordinul O(n). Din punctul de vedere al timpului real de executie, cele doua tipuri de solutii vor fi comparabile, iar in concurs simplitatea solutiei usureaza foarte mult implementarea si depanarea. Din cele prezentate putem concluziona ca sirurile de sufixe sunt o structura de date usor de implementat si foarte utila. In ultimii ani apar la concursuri tot mai multe probleme care necesita cunoasterea acestora. Mai putem observa si faptul ca polonezii propun probleme destul de grele la olimpiade. Speram ca acest articol va va fi de folos si ca de acum inainte sirurile de sufixe vor fi la indemana oricui are nevoie de ele pentru a le folosi intr-un concurs de informatica.
Bibliografie
- Mark Nelson, Fast string searching with suffix trees
- Mircea Pasoi, Multe "smenuri" de programare in C/C++... si nu numai!
- Emilian Miron, LCA - Lowest common ancestor
- Michael A. Bender, Martin Farach-Colton, The LCA Problem Revisited
- Erik Demaine, MIT Advanced Data Structures, Lecture 11, April 2nd, 2003
- Udi Manber, Gene Myers, Suffix arrays: A new method for on-line string searches
- Mohamed Ibrahim Abouelhoda, Stefan Kurtz, Enno Ohlebusch, Replacing suffix trees with enhanced suffix arrays, Journal of Discrete Algorithms 2, 2004
- Thomas Cormen, Charles Leiserson, Ronald Rivest, Introducere in algoritmi, Editura Computer Libris Agora, 2000
- Dana Lica, Arbori de intervale
- Cosmin Negruseri, Cautari ortogonale, GInfo 15/5 (Mai 2005), Editura Agora Media
- BOI 2004
