Arbori de intervale si aplicatii in geometria computationala
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
(Categoria Structuri de date, Autor Dana Lica)
Problema 1
Se considera N (N ≤ 50 000) segmente in plan, dispuse paralel cu axele OX si OY. Sa se determine care este numarul total de intersectii dintre segmente.
In fisierul segment.in se gaseste pe prima linie numarul N de segmente, iar pe fiecare dintre urmatoarele N linii cate patru numere naturale mai mici decat 50 000, reprezentand coordonatele carteziene ale extremitatilor fiecarui segment. Rezultatul se va scrie in segment.out.
Timp de executie: 1 secunda/test.
| segment.in | segment.out | Figura |
|---|---|---|
| 5 2 9 13 9 4 6 12 6 1 2 6 2 5 0 5 8 7 5 7 11 | 4 | 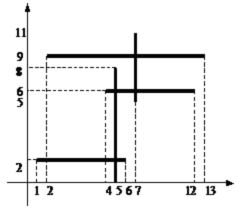 |
Algoritmi de "baleiere" (line sweeping)
Folosind cunostinte generale de geometrie analitica se poate obtine un algoritm O(N2) dar acesta nu se va incadra in limita de timp.
Pentru rezolvarea acestei probleme vom folosi o tehnica cunoscuta sub numele de "baleiere" (sweeping) care este comuna multor algoritmi de geometrie computationala. In baleiere, o dreapta de baleiere verticala, imaginara, traverseaza multimea obiectelor geometrice, de obicei de la stanga la dreapta. Baleierea ofera o metoda pentru ordonarea obiectelor geometrice, plasandu-le intr-o structura de date, pentru obtinerea relatiilor dintre ele.
Algoritmii de baleiere gestioneaza doua multimi de date:
- Starea liniei de baleiere da relatia dintre obiectele intersectate de linia de baleiere
- Lista punct-eveniment este o secventa de coordonate x, ordonate de la stanga la dreapta de obicei, care definesc pozitiile de oprire ale dreptei de baleiere; fiecare astfel de pozitie de oprire se numeste punct eveniment; numai in punctele eveniment se intalnesc modificari ale starii liniei de baleiere; pentru unii algoritmi, lista punct-eveniment este determinata dinamic in timpul executiei algoritmului.
Pentru a rezolva problema, vom deplasa o dreapta de baleiere verticala, imaginara de la stanga la dreapta. Lista punct-eveniment va contine capetele segmentelor orizontale, ce fel de tip sunt (cap stanga sau cap dreapta) si segmentele verticale. Pe masura ce ne deplasam de la stanga la dreapta vom efectua urmatoarele operatii:
- cand intalnim un capat stang, inseram capatul in starile dreptei de baleiere;
- cand intalnim un capat drept, stergem capatul din starile dreptei de baleiere;
- cand intalnim un segment vertical, numarul de intersectii ale acestui segment cu alte segmente orizontale va fi dat de numarul capetelor de intervale care se afla in starile dreptei de baleiere cuprinse intre coordonatele y ale segmentului vertical.
Astfel, starile dreptei de baleiere sunt o structura de date pentru care avem nevoie de urmatoarele operatii:
- INSEREAZA( y ) : insereaza capatul y;
- STERGE( y ) : sterge capatul y;
- INTEROGARE( y1, y2 ) : intoarce numarul de capete cuprinse in intervalul [y1, y2].
Fie MAXC valoarea maxima a coordonatelor capetelor de segmente. Folosind un vector pentru a implementa aceste operatiile descrise mai sus vom obtine o complexitate O(1) pentru primele doua operatii si O(MAXC) pentru cea de-a treia. Astfel, complexitatea va fi O(N*MAXC) in cazul cel mai defavorabil. Putem comprima spatiul [0...MAXC] observand ca doar maxim N din valori din acest interval conteaza, si anume capetele segmentelor orizontale, astfel reducand a treia operatie la O(N), dar algoritmul va avea complexitatea O(N2), ceea ce nu aduce nici o imbunatatire fata de algoritmul trivial.
Aceasta situatie ne indeamna sa cautam o structura de date mai eficienta. O prima varianta ar fi impartirea vectorului in bucati de sqrt(N) reducand complexitatea totala la O(N*√N). In continuare vom prezenta o structura de date care ofera o complexitate logaritmica pentru operatiile descrise mai sus.
Arbori de intervale
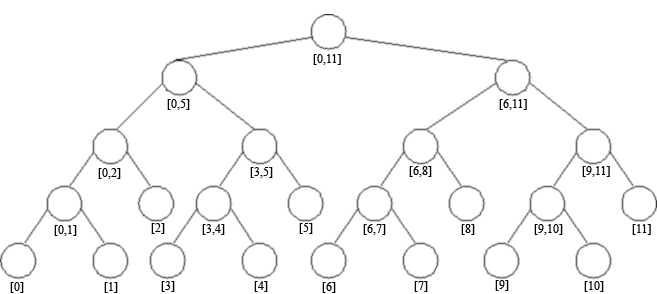
Un arbore de intervale este un arbore binar in care fiecare nod poate avea asociata o structura auxiliara (anumite informatii). Dandu-se doua numere intregi st si dr, cu st < dr, atunci arborele de intervale T(st, dr) se construieste recursiv astfel:
- consideram radacina nod avand asociat intervalul [st, dr];
- daca st < dr atunci vom avea asociat subarborele stang T(st, mij), respectiv subarborele drept T(mij + 1, dr), unde mij este mijlocul intervalului [st, dr].
Intervalul [st, dr] asociat unui nod se numeste interval standard. Frunzele arborelui sunt considerate intervale elementare, ele avand lungimea 1.
Proprietate:
Un arbore de intervale este un arbore binar echilibrat (diferenta absoluta intre adancimea subarborelui stang si cea a subarborelui drept este cel mult 1). Astfel, adancimea unui arbore de intervale care contine N intervale este [log2N] + 1.
Operatii efectuate asupra unui arbore de intervale:
Asupra unui arbore de intervale se pot face doua operatii semnificative: actualizarea, respectiv interogarea unui interval.
Actualizarea unui interval intr-un arbore de intervale
Vom prezenta pseudocodul unei proceduri recursive care insereaza un interval [a, b] intr-un arbore de intervale T(st,dr) cu radacina in nodul nod. Cea mai eficienta metoda de stocare in memorie a unui arbore de intervale este sub forma unui vector folosind aceeasi codificare a nodurilor precum la heap-uri :
procedura ACTUALIZARE(nod, st, dr, a, b)
daca (a <= st) si (dr <= b) atunci
modifica structura auxiliara din nod
altfel
mij = (st + dr) / 2
daca (a <= mij) atunci
ACTUALIZARE(2 * nod, st, mij, a, b)
daca (b > mij) atunci
ACTUALIZARE(2 * nod + 1, mij + 1, dr, a, b)
actualizeaza structura auxiliara din nodul nodInterogarea unui interval intr-un arbore de intervale
Vom prezenta pseudocodul unei proceduri recursive care returneaza informatiile asociate unui interval [a, b] intr-un arbore de intervale T(st,dr) cu radacina in nodul nod.
procedura INTEROGARE(nod, st, dr, a, b)
daca (a <= st) si (dr <= b) atunci
returneaza structura auxiliara din nod
altfel
mij = (st + dr) / 2
daca (a <= mij) atunci
INTEROGARE(2 * nod, st, mij, a, b)
daca (b > mij) atunci
INTEROGARE(2 * nod + 1, mij + 1, dr, a, b)
returneaza structura auxiliara din fiul stang combinata cu cea din fiul dreptVom demonstra in continuare ca operatiile prezentate mai sus au complexitatea O(log2 N) pentru un arbore de N intervale. Este posibil ca intr-un nod sa aiba loc apel atat in fiul stang cat si in cel drept. Acest lucru produce un cost aditional doar prima data cand are loc. Dupa prima "rupere in doua", oricare astfel de "rupere" nu va aduce cost aditional, deoarece unul din fii va fi mereu inclus complet in intervalul [a, b]. Cum inaltimea arborelui, pentru N intervale, este [log2N] + 1, complexitatea operatiilor va fi tot O(log2 N).
Pentru a retine in memorie un arbore de intervale pentru N valori, vom aveam de nevoie de N + N/2 + N/4 + N/8 + ... = 2*N-1 locatii de memorie (sunt 2*N-1 noduri). Deoarece arborele nu este complet, trebuie verificat de fiecare data daca fiii unui nod exista in arbore (aceasta verificare a fost omisa in pseudocodul de mai sus), altfel s-ar incerca accesarea de valori din vector care nu exista. Daca memorie disponibila in timpul concursului este suficienta, se poate declara vectorul care retine arborele de intervale de lungime 2K astfel incat 2K ≥ 2*N-1, simuland astfel un arbore complet si nefiind necesare verificarile mentionate mai sus.
Pentru a rezolva in continuare problema, vom folosi un arbore de intervale pentru a simula in timp logaritmic operatiile facute inainte pe un vector obisnuit. Astfel, in fiecare nod din arborele din intervale vom retine cate capete exista in acel interval. Primele doua operatii vor fi implementate folosind procedura ACTUALIZARE() de mai sus pentru intervalul [y, y] in arborele T(0, MAXC) si adunand 1, respectiv scazand 1 la fiecare nod actualizat. Cea de-a treia operatie poate fi realizata folosind procedura INTEROGARE() pe intervalul [y1, y2]. Astfel complexitatea se reduce la O(N * log2MAXC) Folosind aceeasi tehnica de "comprimare" a coordonatelor se poate obtine o complexitate O(N * log2N).
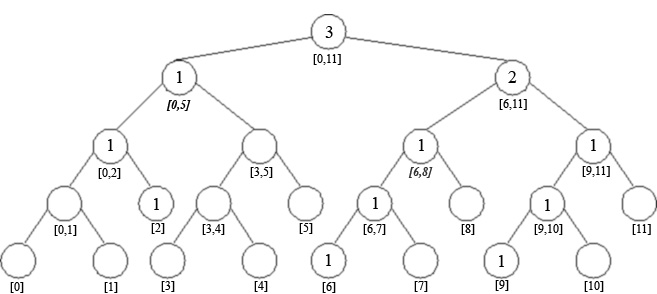
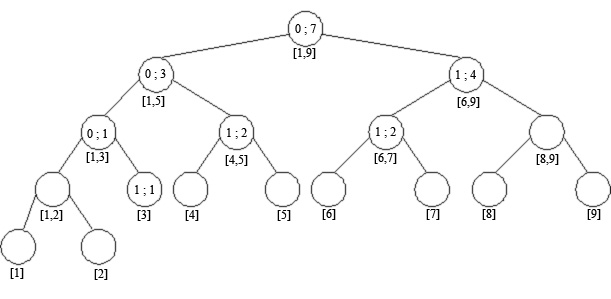
In figura urmatoare este descrisa structura arborelui de intervale, dupa actualizarea pentru intervalele [2, 2], [6, 6] si [9, 9]. Sunt marcate intervalele care conduc la obtinerea numarului de segmente intersectate de primul segment vertical, obtinute in urma interogarii pe intervalul [0, 8].
Problema 2 (Preluata de la IOI 1998, Ziua 2)
Se considera N ≤ 50 000 dreptunghiuri in plan, fiecare avand laturile paralele cu axele OX, OY. Lungimea marginilor (contururilor) reuniunii tuturor dreptunghiurilor se va numi "perimetru". Sa se calculeze perimetrul celor N dreptunghiuri.
In fisierul drept.in se gaseste pe prima linie numarul N de dreptunghiuri, iar pe fiecare din urmatoarele N linii cate patru numere naturale mai mici ca 50 000, reprezentand coordonatele carteziene ale coltului stanga sus, respectiv dreapta jos ale fiecarui dreptunghi. Rezultatul se va scrie in fisierul drept.out.
Timp maxim de executie: 1 secunda/test.
| drept.in | drept.out | Figura |
|---|---|---|
| 3 3 8 8 3 6 10 12 6 12 4 15 1 | 44 | 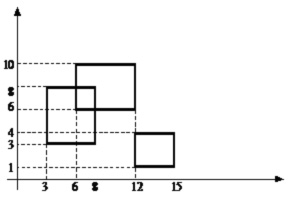 |
Folosind un rationament asemanator ca si la prima problema, constatam necesitatea unui algoritm de baleiere. Vom descompune problema in doua parti: prima data calculam perimetrul folosind doar laturile stanga si dreapta ale dreptunghiurilor pentru a calcula perimetrul pe OY; apoi putem sa rotim dreptunghiurile si folosind aceeasi procedura pt a calcula perimetrul pe OX, folosind doar laturile sus si jos ale dreptunghiurilor.
Fiecare latura (stanga sau dreapta) va fi un punct eveniment. Sortam laturile crescator dupa coordonata x si parcurgem de la stanga la dreapta. Cand intalnim o latura stanga adaugam in starile dreptei de baleiere, intervalul de unitati ocupat de latura pe OY, iar cand intalnim o latura dreapta, eliminam din starile dreptei de baleiere intervalul de unitati ocupat de latura. Intre oricare doua puncte eveniment consecutive are loc o modificare a perimetrului total pe OY. Astfel, dupa fiecare actualizare a starilor dreptei de baleiere se va retine care este numarul de unitati adaugate pana in prezent (nu se tine cont daca o unitate este adaugata de mai multe ori). Vom aduna la perimetrul pe OY total de fiecare data, diferenta absoluta intre numarul de unitati adaugate pana in prezent si valoarea imediat anterioara (dinaintea actualizarii). Asadar, este necesara o structura de date care se efectueze urmatoarele operatii in timp eficient (preferabil logaritmic):
- MARCHEAZA(a, b) : adauga intervalul [a, b];
- DEMARCHEAZA(a, b) : elimina intervalul [a, b];
- INTEROGARE() : returneaza numarul total de coordonate adaugate pana in prezent.
Putem folosi un arbore de intervale pentru a obtine o complexitate O(log2 MAXC) sau O(log2 N) pentru primele doua operatii si O(1) pentru ce-a de treia. In fiecare nod din arbore retinem de cate ori a fost marcat intervalul respectiv si cate unitati din intervalul respectiv au fost marcate. Primele doua operatii pot fi implementate folosind procedura ACTUALIZARE() iar a treia operatie va returna valoarea numarul de unitati care au fost marcate din radacina arborelui de intervale.
In figura urmatoare este descrisa structura arborelui de intervale, dupa adaugarea intervalelor [3, 8] si [6, 10] (un interval [y1, y2] reprezinta intervalul de unitati [y1, y2 - 1] din arbore).
Problema 3
Se dau N ≤ 100 000 puncte in plan de coordonate numere naturale mai mici ca 2 000 000 000. Sa se raspunda la M ≤ 1 000 000 intrebari de forma "cate puncte din cele N exista in dreptunghiul cu coltul stanga sus in (x1, y1) si coltul dreapta jos in (x2, y2)?".
In fisierul puncte.in se vor gasi pe prima linie numerele N si M. Pe urmatoarele N linii se vor gasi coordonatele punctelor. Pe urmatoarele M linii se vor gasi cate patru numere naturale reprezentand coordonatele colturilor dreptunghiurilor. In fisierul puncte.out se vor gasi M numere naturale reprezentand raspunsurile la intrebari.
Timp maxim de executie: 1 secunda/test.
| puncte.in | puncte.out | Figura |
|---|---|---|
| 6 1 2 8 5 3 6 5 8 7 8 1 10 10 4 8 9 4 | 2 | 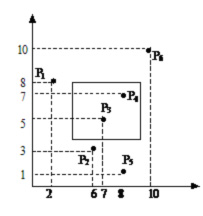 |
Problema determinarii numarului de puncte din interiorul unui dreptunghi este o particularizare bidimensionala pentru problema numita in literatura de specialitate Orthogonal Range Search. Varianta aleasa pentru acest caz consta intr-un arbore de intervale, care permite determinarea numarului de puncte din interiorul unui dreptunghi cu o complexitate O(log22 N).
Astfel, se sorteaza coordonatele x ale punctelor si se construieste un arbore de intervale. Primul nivel al arborelui va contine toate coordonatele x. Cei doi fii ai lui vor contine prima jumatate, respectiv a doua jumatate a punctelor (sortate dupa coordonata x) si asa mai departe. Pentru fiecare interval de coordonate x, se mentin sortate coordonatele y corespunzatoare punctelor care au coordonatele x in intervalul respectiv. Astfel, memoria folosita este O(N * log2N). Pentru a construi efectiv se foloseste o abordare asemanatoare algoritmului de sortare prin interclasare: in fiecare nod, pentru a obtine lista de coordonate y ordonate, se interclaseaza listelele celor doi fii (deja ordonate). Cand se ajunge intr-o frunza, lista nodului este formata dintr-un singur punct.
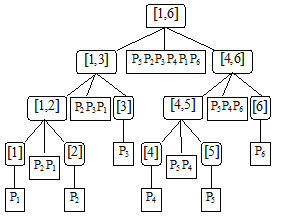
Pentru fiecare dreptunghi, se executa cautarea in arborele de intervale pentru segmentul [x1, x2] (deoarece se folosesc doar cele N coordonate x ale punctelor, se vor potrivi capetele acestui interval folosind cautarea binara la cea mai apropiata coordonata x de fiecare capat). Pentru fiecare interval din arbore atins, se executa doua cautari binare printre coordonatele y corespunzatoare coordonatelor x din acel interval, pentru a determina cate puncte din intervalul respectiv se afla in intervalul [y1, y2] (adica in interiorul dreptunghiului).
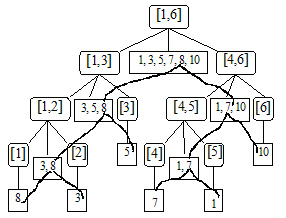
Complexitatea O(log22 N) poate fi redusa, folosind o metoda descoperita independent de Willard si Lueker in anul 1978. Se observa ca pentru fiecare coordonata y dintr-un nod, daca presupunem ca se efectueaza o cautare binara, atunci putem determina in timpul interclasarii pozitia din fiecare fiu pe care o va returna cautarea binara pentru aceeasi valoare. Este evident ca pentru o valoare y dintr-un nod care a provenit dintr-un fiu in timpul interclasarii, exista o unica valoare maxima y' din celalalt fiu astfel incat y' ≤ y. Asadar, tinem pentru fiecare valoare y dintr-un nod doi indici care identifica pozitiile corespunzatoare efectuarii unei cautari binare in fii pentru valoarea y. Astfel, in timpul cautarii, in loc sa se efectueze cautari binare, se pot parcurge acesti indici, care ofera in O(1) pozitia in lista cautata, reducand complexitatea totala la O(log2 N).
Probleme propuse
1. Preluata de la Olimpiada Baltica de Informatica, Polonia 2001
Se considera N ≤ 50 000 dreptunghiuri in plan, fiecare avand laturile paralele cu axele OX, OY. Sa se calculeze aria ocupata de reuniunea celor N dreptunghiuri.
In fisierul drept2.in se gaseste pe prima linie numarul N de dreptunghiuri, iar pe fiecare din urmatoarele N linii cate patru numere naturale mai mici ca 50 000, reprezentand coordonatele carteziene ale coltului stanga sus, respectiv dreapta jos ale fiecarui dreptunghi. Rezultatul se va scrie in fisierul drept2.out.
Timp maxim de executie: 1 secunda/test.
2. Preluata de la Olimpiada Nationala de Informatica, Polonia 2001
Se considera N ≤ 50 000 puncte in plan de coordonate numere naturale mai mici ca 50 000. Sa se determine unde se poate aseza un dreptunghi de lungime DX si latime DY astfel incat numarul de puncte incluse in dreptunghi sa fie maxim.
In fisierul puncte.in se gasesc pe prima linie numerele N, DX si DY. Pe urmatoarele N linii se gasesc coordonatele punctelor. In fisierul puncte.out se vor gasi cinci numere naturale reprezentand coordonatele colturilor stanga sus si dreapta jos ale asezarii dreptunghiului si numarul maxim de puncte din dreptunghi.
Timp maxim de executie: 1 secunda/test.
3. Preluata de la Barajul pentru Lotul National, Romania 2003
Se considera N ≤ 100 000 puncte in plan de coordonate numere naturale mai mici ca 100 000. Sa se determine unde se pot aseza doua dreptunghiuri de lungime DX si latime DY, fara sa se intersecteze, astfel incat numarul de puncte incluse in cele doua dreptunghiuri sa fie maxim.
In fisierul puncte2.in se gasesc pe prima linie numerele N, DX si DY. Pe urmatoarele N linii se gasesc coordonatele punctelor. In fisierul puncte2.out se vor gasi 9 numere naturale reprezentand coordonatele colturilor stanga sus si dreapta jos ale asezarii primului dreptunghi, respectiv a celui de-al doilea, cat si numarul maxim de puncte incluse in ambele dreptunghiuri.
Timp maxim de executie: 1 secunda/test.
4. Preluata de la concursul international USACO January Open, 2004
Se considera N ≤ 250 000 dreptunghiuri in plan, fiecare avand laturile paralele cu axele OX, OY, care nu se intersecteaza si nu se ating, dar pot fi incluse unul in altul. Se numeste "inchisoare" un dreptunghi inconjurat de alte dreptunghiuri. Sa se determine numarul maxim de dreptunghiuri de care poate fi inconjurata o "inchisoare" si cate astfel de "inchisori" maxime exista.
In fisierul inchis.in se gaseste pe prima linie numarul N de dreptunghiuri, iar pe fiecare din urmatoarele N linii cate patru numere naturale mai mici ca 1 000 000 000, reprezentand coordonatele carteziene ale coltului stanga sus, respectiv dreapta jos ale fiecarui dreptunghi. In fisierul inchis.out se gasesc doua numere naturale: numarul maxim de dreptunghiuri de care poate fi inconjurata o "inchisoare" si cate astfel de "inchisori" maxime exista.
Timp maxim de executie: 1 secunda/test.
Nota
Au fost adaugate si implementarile in limbaj Pascal, C ale catorva dintre problemele explicate in articol. Acestea pot fi accesate prin intermediul optiunii "Listeaza atasamente".
