Cautari ortogonale: Structuri de date si aplicatii
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
(Categoria Structuri de date, Autor Cosmin Negruseri)
Introducere
In acest articol voi discuta despre cateva structuri de date folositoare pentru probleme de geometrie, in special pentru probleme ortogonale. Problema de baza ce va fi rezolvata suna in felul urmator: avem n puncte in plan si pentru un anumit dreptunghi ne intereseaza numarul de puncte din acel dreptunghi, sau diverse alte operatii pentru punctele din interiorul sau, cum ar fi suma cheilor punctelor, minimul sau maximul cheilor (daca punctele au asociate cate o cheie). Folosind arbori de intervale putem rezolva aceasta problema, dar vreau sa exemplific ce alte variante mai avem si avantajele lor, precum si aplicatii practice pentru cautarea pe domenii ortogonale. In general, abordarile prezentate mai jos se pot extinde de la cazul unidimensional sau bidimensional, cu usurinta, la cazuri N-dimensionale.
Pentru a intelege cat mai bine ideile si structurile de date prezentate mai departe recomand citirea articolelor [1] si [2].
Structurile prezentate sunt in general statice, adica formam intai structura si apoi rezolvam problema. Structurile de date se pot modifica pentru a suporta inserari si stergeri de puncte, devenind dinamice, dar astfel implementarea se complica. Pentru a simula dinamismul putem insera toate datele de la inceput si sa mai avem un camp boolean in care marcam cu true daca data a fost logic inserata si cu false daca data din nodul respectiv nu a fost inca logic inserata. Aceasta pastreaza complexitatea operatiilor pe structura si ne ajuta in echilibrarea structurilor pentru o eficienta buna a operatiilor.
QuadTree
QuadTree este o structura care organizeaza informatii pentru date multidimensionale, fiind folosita in cartografie, procesarea imaginilor, grafica pe calculator etc. Structura este un arbore ce reprezinta o zona din spatiul N-dimensional (in cazul in care suntem noi interesati, N=2), fiecare nod al arborelui pastreaza o informatie pentru o zona din spatiu, iar nodul are 2N fii care reprezinta fiecare o zona de 2N ori mai mica decat zona parintelui. Zonele fiilor sunt disjuncte, iar reuniunea lor formeaza zona parintelui.
Pentru un QuadTree radacina reprezinta un patrat, iar fii reprezinta cele patru patrate disjuncte si congruente in care se poate imparti patratul initial. Din cate am prezentat pana acum, un QuadTree este infinit, dar pe noi ne intereseaza de obicei intervale foarte mici din plan, si atunci putem sa folosim numai cateva nivele din QuadTree. Cateodata unele noduri din QuadTree nu contin insa nici o informatie si atunci nu avem nevoie sa le folosim pentru ca am folosi memorie in plus.
In problema 3 a zilei 2 a Balcaniadei de Informatica din 1997, se da un QuadTree care reprezinta o imagine colorata alb-negru, de dimensiune 2N * 2N. Daca patratul reprezentat de informatia dintr-un nod al arborelui era de aceeasi culoare, in nod se pastra informatia culorii si nodul nu avea nici un fiu, altfel nodul avea starea indecisa/nedeterminata si avea patru fii.


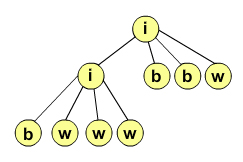
Prima imagine prezinta ordinea in care fii reprezinta patratele, a doua imagine reprezinta o imagine alb-negru, iar a treia este reprezentarea sub forma de QuadTree a acelei imagini.
Pentru a reprezenta n puncte de coordonate intregi in plan cu ajutorul structurii de QuadTree, vom insera care un punct pe rand in QuadTree. Pornim de la un QuadTree gol si inseram un nod recursiv, vedem pentru fiecare patrat care nu are latura de dimensiune unu in care din cele patru patrate din interiorul lui intra punctul nostru. Daca nu exista nod care sa reprezinte acel patrat, il creem noi.
Avantajul pentru structura de QuadTree este usurinta implementarii, dezavantajul este ca structura lui si timpul de raspuns la intrebari depind si de configuratia punctelor, nu numai de numarul total de puncte.
kD-Tree
kD-Tree este o structura de date care organizeaza o multime de puncte in k dimensiuni, imparte spatiul in semispatii astfel ca fiecare nod din arbore reprezinta un paralelipiped si contine in el un punct. Noi suntem interesati de arbori 2D in special. Pentru cazul 2D, primului nod ii va fi asociat intreg planul. Se duce o linie verticala de abscisa x care imparte planul in doua si punctele in doua multimi de cardinal egal. Subarborele din stanga va contine toate punctele din stanga acestei drepte verticale, iar subarborele din dreapta va contine toate punctele din dreapta acestei drepte verticale. Radacinei arborelui din stanga ii va fi asociat semiplanul stang determinat de dreapta verticala, si va contine punctul median dintre punctele din semiplanul stang sortate dupa y. Astfel, la nivel impar punctele vor fi mediane din sirul punctelor sortat dupa x, iar la nivel par punctele vor fi mediane din sirul punctelor sortat dupa y. Pentru mai multe dimensiuni ale spatiului ciclam dupa d1, d2,..., dn si apoi iar d1 ca sa punem elementul median pe nivelul curent. In cazul 2D complexitatea crearii unui asemenea arbore e O(n log n). Pentru a raspunde la query-uri pe un dreptunghi coboram in arbore in fii pentru care domeniul asociat se intersecteaza cu dreptunghiul nostru. Se poate demonstra ca aceasta operatie are timpul de executie in cel mai rau caz O(sqrt(n)).
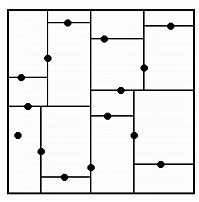
Unele implementari tin puncte numai in frunze, si in nodurile care nu sunt frunze tin numai informatia despre coordonata dreptei care imparte regiunea in doua. Dimensiunile regiunii asociate unui nod pot fi tinute in nod sau pot fi calculate la fiecare operatie pentru a salva spatiu. O alta idee pentru a mari viteza de cautare in arbori kD ar fi sa nu alegem ciclic pe ce directie impartim punctele, ci sa alegem la fiecare pas directia pe care punctele sunt cele mai imprastiate.
Pseudocod pentru constructie:
Nod-kD construiesteArbore(puncte, directie)
daca puncte e vida returneaza null
altfel daca puncte contine un singur punct returneaza Nod-kD(puncte[0])
altfel
x = gasesteMediana(puncte, directie)
// aceasta functie poate fi implementata folosind selectie randomizata
stanga = puncte cu directie <= x;
dreapta = puncte cu directie > x;
t = Nod-kD(x)
t.stanga = construiesteArbore(stanga, (directie + 1) % 2);
t.dreapta = construiesteArbore(dreapta, (directie + 1) % 2);
returneaza tPentru a nu face de fiecare data selectie randomizata putem pleca de la inceput cu doua liste de puncte, una sortata dupa x si cealalta sortata dupa y.
Pseudocod pentru cautare pe domeniu ortogonal (Notam cu Q un dreptunghi):
puncte cauta(nod-kD, Q)
daca Q intersectat cu Nod-kD.domeniu e vid atunci returneaza multimea vida
altfel daca Nod-kD.domeniu e inclus in Q atunci
returneaza punctele din subarborele cu radacina nod-kD
altfel returneaza cauta(nod-kD.stanga, Q) reunita cu cauta(nod-kD.dreapta, Q)Sa vedem care e complexitatea operatiei cauta. Nodurile care sunt total in afara dreptunghiului sau total inauntrul dreptunghiului Q pot cel mult fi de doua ori mai multe decat nodurile care intersecteaza dreptunghiul Q intr-o cautare, pentru ca vizitarea unui nod total in afara dreptunghiului sau unui nod dinauntrul dreptunghiului a pornit de la un nod al carui domeniu intersecteaza dreptunghiul. Pentru analiza ne putem ocupa numai de noduri ale caror domenii intersecteaza dreptunghiul. Pentru a obtine o limita superioara a numarului de zone intersectate putem considera numarul maxim de zone intersectate de o latura a dreptunghiului si sa inmultim acel numar cu patru. Pentru a mai simplifica analiza putem considera nu numarul maxim de zone intersectate de un segment, ci numarul maxim de zone intersectate de o dreapta verticala sau orizontala. Consideram o dreapta verticala, pentru un nod, daca directia de impartire a zonei asociate e verticala atunci dreapta verticala taie sau zona fiului stang sau zona fiului drept, dar nu pe amandoua deodata. Daca dreapta verticala nu intersecteaza zona asociata unui fiu atunci nu va mai intersecta zona nici unui urmas al fiului. In caz contrar intersecteaza ambii fii. Daca coboram la nivelul nepotilor cel mult patru noduri sunt intersectate. In cel mai rau caz intersectam domeniul reprezentat de radacina si putem intersecta cel mult 2i noduri pana la nivelul 2i. Deci in total maxim O(sqrt(n)) noduri sunt parcurse la o operatie cauta.
Avantajul arborilor kD ar fi usurinta in implementare si spatiul de memorie O(n) folosit, dezavantajul ar fi timpul O(sqrt(n)) pentru cautare, dar avand in vedere ca arborii de intervale sau arborii indexati binar au complexitatea O(log2 n) la cautare, timpii sunt comparabili.
Arborii de intervale au fost prezentati in articolul [1] deci nu mai insist asupra lor.
Arborii indexati binar sunt si ei folositori si au fost prezentati [2]. Dezavantajul arborilor indexati binar este ca ei pot fi folositi la numarare si la sume, dar nu la aflarea minimului sau maximului pe un interval. Singura posibilitate cand maximul sau minimul pot fi aflate este atunci cand intervalele pe care facem cautarea sunt nemarginite in sus sau in jos. In schimb la toate structurile despre care am discutat pana acuma putem raspunde in timp subliniar la intrebari despre maxim si minim. Alt dezavantaj este ca daca trebuie sa pastram in spatiul cu n dimensiuni de la 0 pana la N atunci trebuie sa folosim Nn spatiu, insa acest neajuns il putem evita folosind impreuna cu arborele indexat binar si o tabela de dispersie. Facand aceasta folosim numai O(nr log2 N) spatiu pentru nr puncte in plan inserate in structura, pentru cazul unidimensional folosim O(nr * log N) spatiu. Daca folosim structura hash_map sau map din STL obtinem o implementare foarte simpla si memoria folosita este putina.
In continuare, pentru exemplificarea folosirii stucturilor de date voi prezenta niste probleme care voiam sa le propun la concursul de programare Algoritmus, din pacate acest concurs s-a incheiat prematur pentru ca sponsorul nu a mai continuat finantarea premiilor pentru concurenti.
Problema 1
Se dau 1<=n<=30 000 triunghiuri dreptunghice in plan, ele se dau prin trei parametrii x,y,m. Varfurile triunghiurilor o sa fie ( x, y ) ( x + m, y ) si ( x, y + m ). Sa se determine cate perechi de triunghiuri exista, astfel ca primul triunghi din pereche sa fie inclus in al doilea triunghi. ( 0<= x, y, m <= 60 000 )
Timp de executie: 0.5 secunde
Triunghiul determinat de parametrii ( x1,y1,m1 ) e inclus in triunghiul determinat de parametrii ( x2,y2,m2 ) daca si numai daca x2 <= x1, y2 <= y1 si x1 + y1 + m1 <= x2 + y2 + m2. Deci daca facem transformarea ( x1, y1, m1 ) -> ( x1, y1, -x1 - y1 - m1 ) si notam cu ( x1, y1, z1) atunci avem ca triunghiul reprezentat de ( x1, y1, z1 ) e inclus in triunghiul reprezentat de ( x2, y2, z2 ) daca si numai daca x2 <= x1, y2 <= y1, z2 <= z1. Astfel am transformat triunghiurile dreptunghice in puncte din spatiul 3D si perechile de triunghiuri cerute in problema in relatii de dominanta, pentru a afla cate triunghiuri includ triunghiul reprezentat de ( x1, y1, z1 ) trebuie sa vedem cate puncte sunt cuprinse in (-oo, x1] x (-oo, y1] x (-oo, z1]. Pentru a face acest lucru am putea folosi un arbore de intervale 3D care ocupa O(n log2 n) spatiu si are complexitatea O(log3 n) pentru query, dar observatia banala ca putem sorta sirul triunghiurilor dupa coordonata z si abia apoi sa rezolvam problema ne va ajuta. Vom folosi un arbore de intervale 2D sau un quadtree sau un 2D tree (kD tree) in care vom insera ( xi,yi ) in ordinea data de zi. Evident ca la momentul inserarii lui ( xi,yi ) in structura de date toate punctele deja inserate ( xj,yj ) vor proveni din un punct ( xj, yj, zj ) cu zj <= zi, deci nu avem nevoie sa pastram coordonata z a punctelor pentru comparatie. In cazul care implementam problema folosind kd trees vom avea complexitatea O(n log n) la crearea structurii de date si O(sqrt(n)) pentru query, memoria folosita va fi O(n), complexitatea totala a algoritmului O(n log n + n sqrt(n)). Daca folosim arbore de intervale atunci vom folosi O(n log n) timp la crearea structurii si vom avea O(log2 n) pentru query, memoria folosita va fi O(n log n), complexitatea totala va fi O(n log n + n log2 n). Daca folosim tehnica numita "fractional cascading" pentru arbori de intervale atunci reducem complexitatea la O(n log n) pentru intreaga problema.
O alta abordare a problemei bazata tot pe transformarea din triunghiuri in puncte in plan ar fi bazata pe metoda divide si stapaneste. Se impart punctele in doua multimi de dimensiuni egale dupa coordonata z, n/2 puncte au z<=ZMID si celelalte n-n/2 puncte au z>=ZMID, dupa ce s-au numarat relatiile de dominanta din cele doua submultimi, trebuie sa gasim numarul de relatii de dominanta in care un punct e in prima multime si al doilea e in a doua multime. Evident oricare ar fi ( x1, y1, z1 ) in prima multime si ( x2, y2, z2 ) in a doua multime avem ca z1 <= ZMID <= z2 deci mai trebuie sa verificam doar daca x1 <= x2 si y1 <= y2. Daca tinem sirul sortat dupa y si folosim un arbore indexat binar pentru a insera coordonate x in arbore atunci cand in sirul interclasat ordonat dupa y intalnim un punct din prima multime inseram x1 in arborele indexat binar iar cand intalnim un punct din a doua multime atunci intrebam cate coordonate x<=x2 au fost deja inserate in arborele indexat binar daca x <= x2 => si y <= y2 pentru ca a fost inserat in multime mai devreme, in total faza stapaneste a algoritmului ia O(n log n) timp pentru sortarea dupa y si O(n log n) pentru inserarea in arborele indexat binar deci in totalitate algoritmul dureaza O(n log2 n).
A doua metoda poate fi extinsa la numararea incluziunilor de dreptunghiuri. Dreptunghiurile se vor transforma in puncte in 4D, iar cand vom fi la pasul de stapaneste din algoritm vom sorta dupa z si ne va ramane sa determinam cate perechi x1 <= x2 si y1 <= y2, aceasta o vom rezolva folosind un arbore de intervale rafinat prin "fractional cascading", si astfel s-a pastrat complexitatea pasului stapaneste la O(n log n), deci complexitatea totala pentru dreptunghiuri ar fi O(n log2 n). Problema cu dreptunghiuri s-a dat la regionala ACM cu N = 5 000, atunci o singura echipa a rezolvat problema si solutia lor era O(N2).
Problema 2
Se dau doua multimi de puncte de coordonate intregi in plan cu N si M puncte. Punctele din prima multime sunt colorate rosu si punctele din a doua multime sunt colorate albastru. Se cere sa se determine o pereche de puncte, unul rosu si unul albastru, intre care distanta manhattan e minima. Coordonatele punctelor sunt cuprinse intre 0 si 60 000. 1 <= M <= 30 000 si 1 <= N <= 30 000
Timp de executie: 0.5 secunde
Pentru fiecare punct rosu vrem sa stim punctul albastru cel mai apropiat, impartim planul in 4 cadrane cu originea in punctul rosu, vrem sa aflam punctul albastru cel mai apropiat din fiecare cadran. Pentru un punct rosu si un punct albastru din cadranul 1 distanta dintre ele e (xa - xr) + (ya - yr) pentru ca xr < xa si yr < ya, regrupand avem (xa + ya) - (xr + yr). Deci vrem sa gasim punctul (xa, ya) cu proprietatea ca xr <= xa si yr <= ya si suma xa + ya e minima. O solutie ar fi sa folosim un arbore de intervale bidimensional, dar observam ca ambele margini pe domeniul pe care cautam sunt infinite, deci am putea sorta sirurile de puncte descrescator dupa x. Cand punctul (x,y) e albastru inseram in arborele indexat binar la pozitia y cheia x+y, iar cand punctul este rosu facem un query al elementului minim pe intervalul [y, +oo) (evident toate punctele deja inserate in arbore au ordonata mai mare decat y-ul actual). Facem la fel pentru fiecare din cele patru cadrane.
Problema 3
Se dau 1<= N <= 50 000 de dreptunghiuri in plan si se cere sa se determine numarul de perechi de dreptunghiuri care se intersecteaza. Coordonatele varfurilor dreptunghiurilor sunt intregi si cuprinse intre 0 si 60 000.
Timp de executie: 0.5 secunde
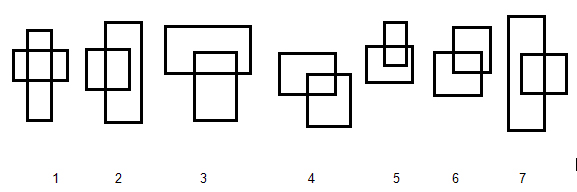
Rezolvam aceasta problema folosind paradigma liniei de baleiere. Sortam dreptunghiurile dupa coordonata x a coltului din dreapta. Dupa cum observam in figura alaturata exista trei pozitii relative ale doua dreptunghiuri care se intersecteaza. Cazurile 1, 2, 4, 5 si 6 se reduc la intersectia laturii verticale din stanga a unui dreptunghi cu latura orizontala de sus a celuilalt dreptunghi, deci acest gen de intersectii pot fi numarate numarand intersectiile intre segmentele orizontale si verticale (aceasta problema a fost deja tratata in articolul [1]). Mai raman cazurile 3 si 7 in care coltul din stanga sus al celui de al doilea dreptunghi e in interiorul primului, acest tip de query il rezolvam cu ajutorul arborilor de intervale, intai inseram in structura toate punctele din dreapta sus ale dreptunghiurilor si apoi pentru fiecare dreptunghi facem query pentru a afla numarul de puncte din interiorul lui.
Problema 4
Se dau 1<= N <= 60 000 de dreptunghiuri in plan, sa se determine un punct care are proprietatea ca este inclus in un numar maxim de dreptunghiuri. Coordonatele varfurilor dreptunghiurilor sunt cuprinse intre 0 si 60 000.
Timp de executie: 0.5 secunde
Reducem problema din plan pe dreapta, daca se da o multime de segmente pe o linie cum determinam un punct care e acoperit de numar maxim de segmente? O sortare a segmentelor dupa primul capat ar rezolva problema, dar solutia aceasta nu e flexibila daca vrem sa adaugam sau sa stergem segmente. Vom folosi un arbore de intervale unidimensional. Numim acoperire canonica a unui interval, intervalele asociate lui in arborele de intervale (stim din articolul [1] ca numarul acestor intervale este maxim log n). In nodurile arborelui de intervale pastram doua atribute: nr si max, nr reprezinta numarul de intervale pentru care intervalul asociat nodului face parte din acoperirea canonica, iar max reprezinta intersectia de intervale nevida inclusa strict in intervalul asociat nodului, cu cardinal maxim. Pentru un nod x, x.max e egal cu maximul dintre x.stanga.max + x.stanga.nr sau x.dreapta.max + x.dreapta.nr. La inserarea sau stergerea din arbore a unui interval avem grija la actualizarea atributelor max si nr. Pentru a determina numarul maxim de segmente ce se intersecteaza putem returna radacina.nr + radacina.
Acum ca putem rezolva problema pe dreapta in mod dinamic sa revenim la problema initiala in plan, vom folosi din nou paradigma liniei de baleiere. Folosim numai segmentele verticale si le ignoram pe cele orizontale. Sortam segmentele verticale dupa x si cand intalnim un segment vertical ce a fost initial latura stanga de dreptunghi atunci adaugam acest segment in arborele de intervale si actualizam daca e nevoie cardinalul intersectiei maxime, daca intalnim un segment vertical care initial era latura din dreapta a unui dreptunghi atunci scoatem acest segment din arborele de intervale. Solutia problemei va avea complexitate O(n log n), O(n log n) in faza de sortare a segmentelor si O(n log n) in faza de inserare in arbore si stergere din arbore.
