#LABAR WAS HERE
Aux
![\[
\underbrace{ \overbrace{1, \hspace{0.2} 2}^{ \text{2}}, \overbrace{1}^{ \text{1}}}_{ \text{3 elemente}} \hspace{0.2cm}
\underbrace{ \overbrace{2, \hspace{0.2} 3}^{ \text{2}}, \overbrace{2}^{ \text{1}}}_{ \text{3 elemente}} \hspace{0.2cm}
\underbrace{ \overbrace{1, 2, 3, 4}^{ \text{4}}, \overbrace{3, 2, 1}^{ \text{3}}}_{ \text{7 elemente}} \hspace{0.2cm}
\underbrace{ \overbrace{2, 3, 4, 5}^{ \text{4}}, \overbrace{4, 3, 2, 1}^{ \text{3}}}_{ \text{7 elemente}} \hspace{0.2cm}
\underbrace{ \overbrace{1, 2, 3, 4, 5, 6}^{ \text{6}}, \overbrace{5, 4, 3, 2, 1}^{ \text{5}}}_{ \text{11 elemente}} \hspace{0.2cm}
\underbrace{ \overbrace{2, 3, 4, 5, 6, 7}^{ \text{6}}, \overbrace{6, 5, 4, 3, 2}^{ \text{5}}}_{ \text{11 elemente}}
\] &
\[
\underbrace{ \overbrace{1, \hspace{0.2} 2}^{ \text{2}}, \overbrace{1}^{ \text{1}}}_{ \text{3 elemente}} \hspace{0.2cm}
\underbrace{ \overbrace{2, \hspace{0.2} 3}^{ \text{2}}, \overbrace{2}^{ \text{1}}}_{ \text{3 elemente}} \hspace{0.2cm}
\underbrace{ \overbrace{1, 2, 3, 4}^{ \text{4}}, \overbrace{3, 2, 1}^{ \text{3}}}_{ \text{7 elemente}} \hspace{0.2cm}
\underbrace{ \overbrace{2, 3, 4, 5}^{ \text{4}}, \overbrace{4, 3, 2, 1}^{ \text{3}}}_{ \text{7 elemente}} \hspace{0.2cm}
\underbrace{ \overbrace{1, 2, 3, 4, 5, 6}^{ \text{6}}, \overbrace{5, 4, 3, 2, 1}^{ \text{5}}}_{ \text{11 elemente}} \hspace{0.2cm}
\underbrace{ \overbrace{2, 3, 4, 5, 6, 7}^{ \text{6}}, \overbrace{6, 5, 4, 3, 2}^{ \text{5}}}_{ \text{11 elemente}}
\] &](http://www.infoarena.ro/static/images/latex/1f961be6f88218c5ffc4a059998af3e6_17.67216pt.gif)
![\[
\underbrace{\overbrace{1, 2, 3, \ldots ,n*2}^{ \text{n*2 elemente} }, \overbrace{(n*2)-1, (n*2)-2 \ldots, 1}^{ \text{n*2-1 elemente}} }_{ \text{n*4-1 elemente}} \hspace{0.2cm}
\underbrace{\overbrace{2, 3, 4, \ldots (n*2+1)+1}^{ \text{n*2 elemente}}, \overbrace{(n*2+1), (n*2+1)-1, \ldots, 1}^{ \text{n*2-1 elemente}} }_{ \text{n*4-1 elemente}}
\] &
\[
\underbrace{\overbrace{1, 2, 3, \ldots ,n*2}^{ \text{n*2 elemente} }, \overbrace{(n*2)-1, (n*2)-2 \ldots, 1}^{ \text{n*2-1 elemente}} }_{ \text{n*4-1 elemente}} \hspace{0.2cm}
\underbrace{\overbrace{2, 3, 4, \ldots (n*2+1)+1}^{ \text{n*2 elemente}}, \overbrace{(n*2+1), (n*2+1)-1, \ldots, 1}^{ \text{n*2-1 elemente}} }_{ \text{n*4-1 elemente}}
\] &](http://www.infoarena.ro/static/images/latex/4677c9e34d4b00b56411aedb061b5d7c_18.61662pt.gif)
![\[
f(n, in, i, p, u, x)=
\begin{cases}
-1, & \text{daca } x \geq n*2\\
x, & \text{daca } p \leq x \leq u, in - \text{par}\\
n-(x-p), & \text{daca } p \leq x \leq u, in - \text{impar}\\
(n-(u-p+1)+1)+(x-p), & \text{daca } x \leq n\\
f(n+1, in+1, i-1, u+1, u+2^{i-1}, x), & \text{altfel}
\end{cases}
\] &
\[
f(n, in, i, p, u, x)=
\begin{cases}
-1, & \text{daca } x \geq n*2\\
x, & \text{daca } p \leq x \leq u, in - \text{par}\\
n-(x-p), & \text{daca } p \leq x \leq u, in - \text{impar}\\
(n-(u-p+1)+1)+(x-p), & \text{daca } x \leq n\\
f(n+1, in+1, i-1, u+1, u+2^{i-1}, x), & \text{altfel}
\end{cases}
\] &](http://www.infoarena.ro/static/images/latex/b33c35ae5bb9c43175b08868b37f1d02_34.50037pt.gif)
#include <iostream>
using namespace std;
int main(){
cout << "Hello World!\n";
return 0;
}![\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &
\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &](http://www.infoarena.ro/static/images/latex/eef80f4248abc3249af6c045a561bf56_13.50015pt.gif)
scrieti "assert(fail)" la inceputul programului la olimpiada si merge de aprox. 10 ori mai rapid programu ca foloseste mai multe core-uri(merge in c++, dar si in c)
h1. KAKTUS
MULTE SMENURI DE PROGRAMARE IN C/C++... SI NU NUMAI!!!!!!!
Furnicuţa şi-a construit un depozit pentru grăunţe .pdf
oof
O zi frumoasa in cutiuţa cu năsip
Tudor Gălăţan a.k.a. How to be or not to be something.
<tex
| Ionescu | 12 | Constanta | Popescu | 24 | Bucuresti | Popescu | 24 | Bucuresti |
log me
LaTeX pe mai multe rânduri:
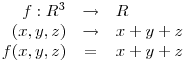
sau:
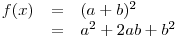
Tabel mic:d
| A | B | A->B |
| 0 | 2 | 3 |
Tabel mare:
| A | B | A->B |
| 1 | 2 | 3 |
Tabel si mai mare:
| A | B | A->B |
| 1 | 2 | 3 |
Diacritice:
Straşnic de îngâmfat, ţăranul crapă streaşina.
Straşnic de îngâmfat, ţăranul crapă streaşina.
In Windows XP sp2 cu IE6 fara update de font se vede asa:

Ordered list:
- 1st item
- 2nd item
Use only F/OSS, Microsft sucks ;) just because I say so.
Love Linux, beacuse I say so.
However, on a GNU system NEVER type <b>sudo make me sandwich</b> , and expect the results...
¡Entendido, amigo!
x
y
a weirdo put this text here
yey im playing with bleach
hi my name is cosine dabe ur frind dont tuch my gotye
Vivi's blog
* 
p. 
Avem suport pentru  !
!
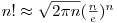
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
| test | test |
Worship me
Feel free to plghay around, but Big Brother is watching you.
What does this button do?
lalallaa
Intrebare: cum poti seta culoarea cu care scrii?
Uite asa: scris cu rosu
Siteul sub IE 7 -- vezi pagina dedicata
Siteul sub FF 2 - mica problema panoul de 'editeaza', 'vezi istoria', 'sterge' etc (in IE7 panoul nu se suprapune)

[test]
OMG test, good work people :D
Acuma doar trebuie putin stimulata comunitatea
[/test]
Interesting choice of words.
a very bold MAN
CAPSOMANII-I DESPISE THEM
gasise pe-un teren viran,
un geamantan.
si-n geamantan,
un pachet.
si in pachet,
un pachetel gasise el.
si-n pachetel,
alt pachetel.
si-un pachetel in pachetel,
legat cu funde elegante.
si-n pachetel...vreo 40 de diamante...
...
Adio voi...va las si plec fiindca mi-e dor...
si a plecat Apolodor
!!!<>
tralalala blablabla lala
salut, aici poate sa scrie oricine ce vrea? Robert
| 1 | 2 | 3 |
|---|---|---|
| unu | doi | trei |
| 1... unu | 2... doi | 3... trei |
Moraru Ionut has been here. :))
shnako was here :)
:) gosh...
inca unul, de tipul cel mai heyyyyyyyyyy prost din corcodus, se joaca cu in nisip.. ura ...
cel mai prost din corcodus a terminat... altcineva?:D
tot el: atentie fratilor ne urmareste big brother 3 (sau 4)
Care imi da o lopata ? :)
// comentariu
#include <cstdio> // comment1
// comment2
int main()
{
return 0;
}| Latura 1 | Latura 2 | Latura 3 | Latura 4 | Latura 2 | Latura 3 | Latura 1 |
|---|---|---|---|---|---|---|
| 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 |
&6 7 8&
# Hello
## Hello 2
### Hello 3

Subsir 2
(problema grea clasa a 9a, problema medie clasa a 10a, problema usoara clasele 11-12)
Problema poate fi considerata asemanatoare cu cea a celui mai lung subsir crescator, avand o rezolvare similara de complexitatea O(N2) folosind metoda programarii dinamice.
Se vor construi doi vectori:
- Ai = lungimea celui mai scurt subsir crescator maximal care incepe cu pozitia i
- Ti = urmatorul element dupa pozitia i in cel mai scurt subsir crescator maximal care incepe cu i (pentru reconstiutire)
Pentru fiecare i, se va cauta un j > i astfel incat Vi ≤ Vj (unde V este vectorul de numere) si se alege acela cu Aj minim, Ai devenind Aj+1, iar Ti devine j. Daca nu exista nici un j, Ai se initializeaza cu 1 si Ti cu i.
Ca sirul construit sa fie maximal trebuie ca atunci cand verificam j-urile pentru un i fixat, j-ul respectiv sa fie "dominant", in sensul ca sa nu existe un i < k < j astfel incat Vi ≤ Vk ≤ Vj, deoarece sirul construit cu primul element in i si al doilea in j ar putea fi extins inserand k intre i si j. Verificarea pentru acest k se poate face in O(N), obtinand o solutie O(N3) care ar fi adus 50-60p. Pentru a face verificarea in O(1), facem observatia ca ne intereseaza doar acel Vk minim care este ≥ Vi. Pe masura ce se avanseaza cu variabila j, se pastreaza o variabila min, reprezentand minimul dintre valorile Vj parcurse pana acum, care sunt ≥ Vi.
Astfel, cand se ajunge la un j, se verifica inainte daca Vj < min (conditie necesara pentru a construi un sir maximal). Un ultim detaliu in solutie este obtinerea solutiei minime din punct de vedere lexicografic. Cand se selecteaza j-ul pentru fiecare i, pe langa faptul ca se alege acela cu Aj minim, in caz de egalitate se va alege acela cu valoarea Vj minima. Selectarea este corecta deoarece nu vor exista j1, j2 cu Aj1 si Aj2 minim , iar Vj1 = Vj2.
Problema se poate rezolva mai bine intr-o complexitate O(N*lg2 N) folosind structuri de date avansate, astfel transformandu-se intr-o problema de clasele 11-12 grea, sau chiar o problema de finala. Lasam aceasta rezolvare ca exercitiu pentru cititor.
Sum
(problema usoara, clasa a 10a)
Vom face o prima observatie:
- (n, d) = 1 <=> (n, n - d) = 1, (n, n + d) = 1
Fie a = phi (n), indicatorul lui Euler. Fie b numarul de numere prime cu n cuprinse intre n si 2 * n.
Deoarece (n, d) = 1 <=> (n, n + d) = 1, a ≤ b. Deoarece (n, d) = 1 <=> (n, n - d) = 1, b ≤ a => b = a. Fie x1, x2, .. xa numerele < n si prime cu n => numerele cuprinse intre n si 2 * n si prime cu n vor fi x1 + n, x2 + n, .. xa + n.
Conform observatiei facute, (n, n - x1) = 1, (n, n - x2) = 1, .. (n, n - xa) = 1 =>
xa = n - x1 <=> x1 + xa = n
xa-1 = n - x2 <=> x2 + xa-1 = n
...
x1 = n - xa <=> xa + x1 = n
Fie S1 suma numerelor prime cu n si mai mici ca n, fie S2 suma numerelor prime cu n, cuprinse intre n si 2 * n.
Adunand cele a egalitati, obtinem 2 * S1 = a * n => S1 = (a * n) / 2.
S2 = a * n + S1 => S1 + S2 = 2 * a * n.
Se foloseste o singura data ciurul lui Erathostene pentru a determina functia phi pentru toate intrebarile. Se poate consulta articolul despre cirulul lui Erathostene.
Pavare 2
(problema grea, clasa a 10a)
Problema se rezolva cu programare dinamica. Utilizam urmatoare structura de date:
- V[i][j][0] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie albe
- V[i][j][1] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie negre
Relatiile de recurenta sunt acum usor de dedus. Odata calculata matricea putem raspunde foarte usor primei cerinte, facand suma V[N][i][0] (pentru 1 ≤ i ≤ A) si V[N][i][1] pentru (1 ≤ i ≤ B).
Pentru a 2-a cerinta incercam sa construim a K-a secventa lexicografica de la inceput catre sfarsit. Astfel, la fiecare pas incercam sa punem o segventa de tipul '0...01' care sa contina un numar maxim de '0'. Daca la pasul curent nu putem pune nici un '0' atunci vom pune o secventa de tipul '1..1' care sa contina un numar minim de 1. Numarul de '0'-uri sau de '1' pe care il punem il vom calcula cu ajutorul matricei precalculate la prima cerinta. Astfel, daca putem pune p de '0' inseamna ca numarul de posibilitati pentru a completa restul solutiei daca punem cel putin p de '0' la inceput este mai mare sau egal cu K. Alegem cel mai mare numar p cu proprietatea de mai sus. Daca p nu exista, incercam sa punem cat mai putini '1' in aceeasi maniera. Continuam apoi cu restul secventei, iar din K scadem numarul de solutii peste care am "sarit".
Tare de tot acest sandbox :)
* Re: chiar ca e! poti sa te joci cu css aici :)
![\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &
\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &](http://www.infoarena.ro/static/images/latex/eef80f4248abc3249af6c045a561bf56_13.50015pt.gif)
scrieti "assert(fail)" la inceputul programului la olimpiada si merge de aprox. 10 ori mai rapid programu ca foloseste mai multe core-uri(merge in c++, dar si in c)
h1. KAKTUS
MULTE SMENURI DE PROGRAMARE IN C/C++... SI NU NUMAI!!!!!!!
Furnicuţa şi-a construit un depozit pentru grăunţe .pdf
oof
O zi frumoasa in cutiuţa cu năsip
Tudor Gălăţan a.k.a. How to be or not to be something.
<tex
| Ionescu | 12 | Constanta | Popescu | 24 | Bucuresti | Popescu | 24 | Bucuresti |
log me
LaTeX pe mai multe rânduri:
sau:
Tabel mic:d
| A | B | A->B |
| 0 | 2 | 3 |
Tabel mare:
| A | B | A->B |
| 1 | 2 | 3 |
Tabel si mai mare:
| A | B | A->B |
| 1 | 2 | 3 |
Diacritice:
Straşnic de îngâmfat, ţăranul crapă streaşina.
Straşnic de îngâmfat, ţăranul crapă streaşina.
In Windows XP sp2 cu IE6 fara update de font se vede asa:

Ordered list:
- 1st item
- 2nd item
Use only F/OSS, Microsft sucks ;) just because I say so.
Love Linux, beacuse I say so.
However, on a GNU system NEVER type <b>sudo make me sandwich</b> , and expect the results...
¡Entendido, amigo!
x
y
a weirdo put this text here
yey im playing with bleach
hi my name is cosine dabe ur frind dont tuch my gotye
Vivi's blog
* 
p. 
Avem suport pentru  !
!
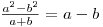
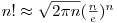
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
| test | test |
Worship me
Feel free to plghay around, but Big Brother is watching you.
What does this button do?
lalallaa
Intrebare: cum poti seta culoarea cu care scrii?
Uite asa: scris cu rosu
Siteul sub IE 7 -- vezi pagina dedicata
Siteul sub FF 2 - mica problema panoul de 'editeaza', 'vezi istoria', 'sterge' etc (in IE7 panoul nu se suprapune)

[test]
OMG test, good work people :D
Acuma doar trebuie putin stimulata comunitatea
[/test]
Interesting choice of words.
a very bold MAN
CAPSOMANII-I DESPISE THEM
gasise pe-un teren viran,
un geamantan.
si-n geamantan,
un pachet.
si in pachet,
un pachetel gasise el.
si-n pachetel,
alt pachetel.
si-un pachetel in pachetel,
legat cu funde elegante.
si-n pachetel...vreo 40 de diamante...
...
Adio voi...va las si plec fiindca mi-e dor...
si a plecat Apolodor
!!!<>
tralalala blablabla lala
salut, aici poate sa scrie oricine ce vrea? Robert
| 1 | 2 | 3 |
|---|---|---|
| unu | doi | trei |
| 1... unu | 2... doi | 3... trei |
Moraru Ionut has been here. :))
shnako was here :)
:) gosh...
inca unul, de tipul cel mai heyyyyyyyyyy prost din corcodus, se joaca cu in nisip.. ura ...
cel mai prost din corcodus a terminat... altcineva?:D
tot el: atentie fratilor ne urmareste big brother 3 (sau 4)
Care imi da o lopata ? :)
// comentariu
#include <cstdio> // comment1
// comment2
int main()
{
return 0;
}| Latura 1 | Latura 2 | Latura 3 | Latura 4 | Latura 2 | Latura 3 | Latura 1 |
|---|---|---|---|---|---|---|
| 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 |
&6 7 8&
# Hello
## Hello 2
### Hello 3

Subsir 2
(problema grea clasa a 9a, problema medie clasa a 10a, problema usoara clasele 11-12)
Problema poate fi considerata asemanatoare cu cea a celui mai lung subsir crescator, avand o rezolvare similara de complexitatea O(N2) folosind metoda programarii dinamice.
Se vor construi doi vectori:
- Ai = lungimea celui mai scurt subsir crescator maximal care incepe cu pozitia i
- Ti = urmatorul element dupa pozitia i in cel mai scurt subsir crescator maximal care incepe cu i (pentru reconstiutire)
Pentru fiecare i, se va cauta un j > i astfel incat Vi ≤ Vj (unde V este vectorul de numere) si se alege acela cu Aj minim, Ai devenind Aj+1, iar Ti devine j. Daca nu exista nici un j, Ai se initializeaza cu 1 si Ti cu i.
Ca sirul construit sa fie maximal trebuie ca atunci cand verificam j-urile pentru un i fixat, j-ul respectiv sa fie "dominant", in sensul ca sa nu existe un i < k < j astfel incat Vi ≤ Vk ≤ Vj, deoarece sirul construit cu primul element in i si al doilea in j ar putea fi extins inserand k intre i si j. Verificarea pentru acest k se poate face in O(N), obtinand o solutie O(N3) care ar fi adus 50-60p. Pentru a face verificarea in O(1), facem observatia ca ne intereseaza doar acel Vk minim care este ≥ Vi. Pe masura ce se avanseaza cu variabila j, se pastreaza o variabila min, reprezentand minimul dintre valorile Vj parcurse pana acum, care sunt ≥ Vi.
Astfel, cand se ajunge la un j, se verifica inainte daca Vj < min (conditie necesara pentru a construi un sir maximal). Un ultim detaliu in solutie este obtinerea solutiei minime din punct de vedere lexicografic. Cand se selecteaza j-ul pentru fiecare i, pe langa faptul ca se alege acela cu Aj minim, in caz de egalitate se va alege acela cu valoarea Vj minima. Selectarea este corecta deoarece nu vor exista j1, j2 cu Aj1 si Aj2 minim , iar Vj1 = Vj2.
Problema se poate rezolva mai bine intr-o complexitate O(N*lg2 N) folosind structuri de date avansate, astfel transformandu-se intr-o problema de clasele 11-12 grea, sau chiar o problema de finala. Lasam aceasta rezolvare ca exercitiu pentru cititor.
Sum
(problema usoara, clasa a 10a)
Vom face o prima observatie:
- (n, d) = 1 <=> (n, n - d) = 1, (n, n + d) = 1
Fie a = phi (n), indicatorul lui Euler. Fie b numarul de numere prime cu n cuprinse intre n si 2 * n.
Deoarece (n, d) = 1 <=> (n, n + d) = 1, a ≤ b. Deoarece (n, d) = 1 <=> (n, n - d) = 1, b ≤ a => b = a. Fie x1, x2, .. xa numerele < n si prime cu n => numerele cuprinse intre n si 2 * n si prime cu n vor fi x1 + n, x2 + n, .. xa + n.
Conform observatiei facute, (n, n - x1) = 1, (n, n - x2) = 1, .. (n, n - xa) = 1 =>
xa = n - x1 <=> x1 + xa = n
xa-1 = n - x2 <=> x2 + xa-1 = n
...
x1 = n - xa <=> xa + x1 = n
Fie S1 suma numerelor prime cu n si mai mici ca n, fie S2 suma numerelor prime cu n, cuprinse intre n si 2 * n.
Adunand cele a egalitati, obtinem 2 * S1 = a * n => S1 = (a * n) / 2.
S2 = a * n + S1 => S1 + S2 = 2 * a * n.
Se foloseste o singura data ciurul lui Erathostene pentru a determina functia phi pentru toate intrebarile. Se poate consulta articolul despre cirulul lui Erathostene.
Pavare 2
(problema grea, clasa a 10a)
Problema se rezolva cu programare dinamica. Utilizam urmatoare structura de date:
- V[i][j][0] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie albe
- V[i][j][1] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie negre
Relatiile de recurenta sunt acum usor de dedus. Odata calculata matricea putem raspunde foarte usor primei cerinte, facand suma V[N][i][0] (pentru 1 ≤ i ≤ A) si V[N][i][1] pentru (1 ≤ i ≤ B).
Pentru a 2-a cerinta incercam sa construim a K-a secventa lexicografica de la inceput catre sfarsit. Astfel, la fiecare pas incercam sa punem o segventa de tipul '0...01' care sa contina un numar maxim de '0'. Daca la pasul curent nu putem pune nici un '0' atunci vom pune o secventa de tipul '1..1' care sa contina un numar minim de 1. Numarul de '0'-uri sau de '1' pe care il punem il vom calcula cu ajutorul matricei precalculate la prima cerinta. Astfel, daca putem pune p de '0' inseamna ca numarul de posibilitati pentru a completa restul solutiei daca punem cel putin p de '0' la inceput este mai mare sau egal cu K. Alegem cel mai mare numar p cu proprietatea de mai sus. Daca p nu exista, incercam sa punem cat mai putini '1' in aceeasi maniera. Continuam apoi cu restul secventei, iar din K scadem numarul de solutii peste care am "sarit".
Tare de tot acest sandbox :)
* Re: chiar ca e! poti sa te joci cu css aici :)
![\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &
\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &](http://www.infoarena.ro/static/images/latex/eef80f4248abc3249af6c045a561bf56_13.50015pt.gif)
scrieti "assert(fail)" la inceputul programului la olimpiada si merge de aprox. 10 ori mai rapid programu ca foloseste mai multe core-uri(merge in c++, dar si in c)
h1. KAKTUS
MULTE SMENURI DE PROGRAMARE IN C/C++... SI NU NUMAI!!!!!!!
Furnicuţa şi-a construit un depozit pentru grăunţe .pdf
oof
O zi frumoasa in cutiuţa cu năsip
Tudor Gălăţan a.k.a. How to be or not to be something.
<tex
| Ionescu | 12 | Constanta | Popescu | 24 | Bucuresti | Popescu | 24 | Bucuresti |
log me
LaTeX pe mai multe rânduri:
sau:
Tabel mic:d
| A | B | A->B |
| 0 | 2 | 3 |
Tabel mare:
| A | B | A->B |
| 1 | 2 | 3 |
Tabel si mai mare:
| A | B | A->B |
| 1 | 2 | 3 |
Diacritice:
Straşnic de îngâmfat, ţăranul crapă streaşina.
Straşnic de îngâmfat, ţăranul crapă streaşina.
In Windows XP sp2 cu IE6 fara update de font se vede asa:

Ordered list:
- 1st item
- 2nd item
Use only F/OSS, Microsft sucks ;) just because I say so.
Love Linux, beacuse I say so.
However, on a GNU system NEVER type <b>sudo make me sandwich</b> , and expect the results...
¡Entendido, amigo!
x
y
a weirdo put this text here
yey im playing with bleach
hi my name is cosine dabe ur frind dont tuch my gotye
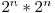
Vivi's blog
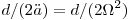
* 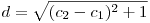
p. 
Avem suport pentru 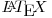 !
!
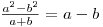
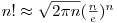
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
| test | test |
Worship me
Feel free to plghay around, but Big Brother is watching you.
What does this button do?
lalallaa
Intrebare: cum poti seta culoarea cu care scrii?
Uite asa: scris cu rosu
Siteul sub IE 7 -- vezi pagina dedicata
Siteul sub FF 2 - mica problema panoul de 'editeaza', 'vezi istoria', 'sterge' etc (in IE7 panoul nu se suprapune)

[test]
OMG test, good work people :D
Acuma doar trebuie putin stimulata comunitatea
[/test]
Interesting choice of words.
a very bold MAN
CAPSOMANII-I DESPISE THEM
gasise pe-un teren viran,
un geamantan.
si-n geamantan,
un pachet.
si in pachet,
un pachetel gasise el.
si-n pachetel,
alt pachetel.
si-un pachetel in pachetel,
legat cu funde elegante.
si-n pachetel...vreo 40 de diamante...
...
Adio voi...va las si plec fiindca mi-e dor...
si a plecat Apolodor
!!!<>
tralalala blablabla lala
salut, aici poate sa scrie oricine ce vrea? Robert
| 1 | 2 | 3 |
|---|---|---|
| unu | doi | trei |
| 1... unu | 2... doi | 3... trei |
Moraru Ionut has been here. :))
shnako was here :)
:) gosh...
inca unul, de tipul cel mai heyyyyyyyyyy prost din corcodus, se joaca cu in nisip.. ura ...
cel mai prost din corcodus a terminat... altcineva?:D
tot el: atentie fratilor ne urmareste big brother 3 (sau 4)
Care imi da o lopata ? :)
// comentariu
#include <cstdio> // comment1
// comment2
int main()
{
return 0;
}| Latura 1 | Latura 2 | Latura 3 | Latura 4 | Latura 2 | Latura 3 | Latura 1 |
|---|---|---|---|---|---|---|
| 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 |
&6 7 8&
# Hello
## Hello 2
### Hello 3

Subsir 2
(problema grea clasa a 9a, problema medie clasa a 10a, problema usoara clasele 11-12)
Problema poate fi considerata asemanatoare cu cea a celui mai lung subsir crescator, avand o rezolvare similara de complexitatea O(N2) folosind metoda programarii dinamice.
Se vor construi doi vectori:
- Ai = lungimea celui mai scurt subsir crescator maximal care incepe cu pozitia i
- Ti = urmatorul element dupa pozitia i in cel mai scurt subsir crescator maximal care incepe cu i (pentru reconstiutire)
Pentru fiecare i, se va cauta un j > i astfel incat Vi ≤ Vj (unde V este vectorul de numere) si se alege acela cu Aj minim, Ai devenind Aj+1, iar Ti devine j. Daca nu exista nici un j, Ai se initializeaza cu 1 si Ti cu i.
Ca sirul construit sa fie maximal trebuie ca atunci cand verificam j-urile pentru un i fixat, j-ul respectiv sa fie "dominant", in sensul ca sa nu existe un i < k < j astfel incat Vi ≤ Vk ≤ Vj, deoarece sirul construit cu primul element in i si al doilea in j ar putea fi extins inserand k intre i si j. Verificarea pentru acest k se poate face in O(N), obtinand o solutie O(N3) care ar fi adus 50-60p. Pentru a face verificarea in O(1), facem observatia ca ne intereseaza doar acel Vk minim care este ≥ Vi. Pe masura ce se avanseaza cu variabila j, se pastreaza o variabila min, reprezentand minimul dintre valorile Vj parcurse pana acum, care sunt ≥ Vi.
Astfel, cand se ajunge la un j, se verifica inainte daca Vj < min (conditie necesara pentru a construi un sir maximal). Un ultim detaliu in solutie este obtinerea solutiei minime din punct de vedere lexicografic. Cand se selecteaza j-ul pentru fiecare i, pe langa faptul ca se alege acela cu Aj minim, in caz de egalitate se va alege acela cu valoarea Vj minima. Selectarea este corecta deoarece nu vor exista j1, j2 cu Aj1 si Aj2 minim , iar Vj1 = Vj2.
Problema se poate rezolva mai bine intr-o complexitate O(N*lg2 N) folosind structuri de date avansate, astfel transformandu-se intr-o problema de clasele 11-12 grea, sau chiar o problema de finala. Lasam aceasta rezolvare ca exercitiu pentru cititor.
Sum
(problema usoara, clasa a 10a)
Vom face o prima observatie:
- (n, d) = 1 <=> (n, n - d) = 1, (n, n + d) = 1
Fie a = phi (n), indicatorul lui Euler. Fie b numarul de numere prime cu n cuprinse intre n si 2 * n.
Deoarece (n, d) = 1 <=> (n, n + d) = 1, a ≤ b. Deoarece (n, d) = 1 <=> (n, n - d) = 1, b ≤ a => b = a. Fie x1, x2, .. xa numerele < n si prime cu n => numerele cuprinse intre n si 2 * n si prime cu n vor fi x1 + n, x2 + n, .. xa + n.
Conform observatiei facute, (n, n - x1) = 1, (n, n - x2) = 1, .. (n, n - xa) = 1 =>
xa = n - x1 <=> x1 + xa = n
xa-1 = n - x2 <=> x2 + xa-1 = n
...
x1 = n - xa <=> xa + x1 = n
Fie S1 suma numerelor prime cu n si mai mici ca n, fie S2 suma numerelor prime cu n, cuprinse intre n si 2 * n.
Adunand cele a egalitati, obtinem 2 * S1 = a * n => S1 = (a * n) / 2.
S2 = a * n + S1 => S1 + S2 = 2 * a * n.
Se foloseste o singura data ciurul lui Erathostene pentru a determina functia phi pentru toate intrebarile. Se poate consulta articolul despre cirulul lui Erathostene.
Pavare 2
(problema grea, clasa a 10a)
Problema se rezolva cu programare dinamica. Utilizam urmatoare structura de date:
- V[i][j][0] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie albe
- V[i][j][1] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie negre
Relatiile de recurenta sunt acum usor de dedus. Odata calculata matricea putem raspunde foarte usor primei cerinte, facand suma V[N][i][0] (pentru 1 ≤ i ≤ A) si V[N][i][1] pentru (1 ≤ i ≤ B).
Pentru a 2-a cerinta incercam sa construim a K-a secventa lexicografica de la inceput catre sfarsit. Astfel, la fiecare pas incercam sa punem o segventa de tipul '0...01' care sa contina un numar maxim de '0'. Daca la pasul curent nu putem pune nici un '0' atunci vom pune o secventa de tipul '1..1' care sa contina un numar minim de 1. Numarul de '0'-uri sau de '1' pe care il punem il vom calcula cu ajutorul matricei precalculate la prima cerinta. Astfel, daca putem pune p de '0' inseamna ca numarul de posibilitati pentru a completa restul solutiei daca punem cel putin p de '0' la inceput este mai mare sau egal cu K. Alegem cel mai mare numar p cu proprietatea de mai sus. Daca p nu exista, incercam sa punem cat mai putini '1' in aceeasi maniera. Continuam apoi cu restul secventei, iar din K scadem numarul de solutii peste care am "sarit".
Tare de tot acest sandbox :)
* Re: chiar ca e! poti sa te joci cu css aici :)
![\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &
\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &](http://www.infoarena.ro/static/images/latex/eef80f4248abc3249af6c045a561bf56_13.50015pt.gif)
scrieti "assert(fail)" la inceputul programului la olimpiada si merge de aprox. 10 ori mai rapid programu ca foloseste mai multe core-uri(merge in c++, dar si in c)
h1. KAKTUS
MULTE SMENURI DE PROGRAMARE IN C/C++... SI NU NUMAI!!!!!!!
Furnicuţa şi-a construit un depozit pentru grăunţe .pdf
oof
O zi frumoasa in cutiuţa cu năsip
Tudor Gălăţan a.k.a. How to be or not to be something.
<tex
| Ionescu | 12 | Constanta | Popescu | 24 | Bucuresti | Popescu | 24 | Bucuresti |
log me
LaTeX pe mai multe rânduri:
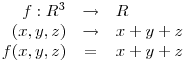
sau:
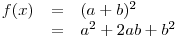
Tabel mic:d
| A | B | A->B |
| 0 | 2 | 3 |
Tabel mare:
| A | B | A->B |
| 1 | 2 | 3 |
Tabel si mai mare:
| A | B | A->B |
| 1 | 2 | 3 |
Diacritice:
Straşnic de îngâmfat, ţăranul crapă streaşina.
Straşnic de îngâmfat, ţăranul crapă streaşina.
In Windows XP sp2 cu IE6 fara update de font se vede asa:

Ordered list:
- 1st item
- 2nd item
Use only F/OSS, Microsft sucks ;) just because I say so.
Love Linux, beacuse I say so.
However, on a GNU system NEVER type <b>sudo make me sandwich</b> , and expect the results...
¡Entendido, amigo!
x
y
a weirdo put this text here
yey im playing with bleach
hi my name is cosine dabe ur frind dont tuch my gotye
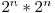
Vivi's blog
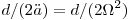
* 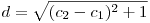
p. 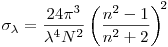
Avem suport pentru 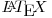 !
!
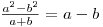
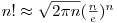
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
| test | test |
Worship me
Feel free to plghay around, but Big Brother is watching you.
What does this button do?
lalallaa
Intrebare: cum poti seta culoarea cu care scrii?
Uite asa: scris cu rosu
Siteul sub IE 7 -- vezi pagina dedicata
Siteul sub FF 2 - mica problema panoul de 'editeaza', 'vezi istoria', 'sterge' etc (in IE7 panoul nu se suprapune)

[test]
OMG test, good work people :D
Acuma doar trebuie putin stimulata comunitatea
[/test]
Interesting choice of words.
a very bold MAN
CAPSOMANII-I DESPISE THEM
gasise pe-un teren viran,
un geamantan.
si-n geamantan,
un pachet.
si in pachet,
un pachetel gasise el.
si-n pachetel,
alt pachetel.
si-un pachetel in pachetel,
legat cu funde elegante.
si-n pachetel...vreo 40 de diamante...
...
Adio voi...va las si plec fiindca mi-e dor...
si a plecat Apolodor
!!!<>
tralalala blablabla lala
salut, aici poate sa scrie oricine ce vrea? Robert
| 1 | 2 | 3 |
|---|---|---|
| unu | doi | trei |
| 1... unu | 2... doi | 3... trei |
Moraru Ionut has been here. :))
shnako was here :)
:) gosh...
inca unul, de tipul cel mai heyyyyyyyyyy prost din corcodus, se joaca cu in nisip.. ura ...
cel mai prost din corcodus a terminat... altcineva?:D
tot el: atentie fratilor ne urmareste big brother 3 (sau 4)
Care imi da o lopata ? :)
// comentariu
#include <cstdio> // comment1
// comment2
int main()
{
return 0;
}| Latura 1 | Latura 2 | Latura 3 | Latura 4 | Latura 2 | Latura 3 | Latura 1 |
|---|---|---|---|---|---|---|
| 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 |
&6 7 8&
# Hello
## Hello 2
### Hello 3

Subsir 2
(problema grea clasa a 9a, problema medie clasa a 10a, problema usoara clasele 11-12)
Problema poate fi considerata asemanatoare cu cea a celui mai lung subsir crescator, avand o rezolvare similara de complexitatea O(N2) folosind metoda programarii dinamice.
Se vor construi doi vectori:
- Ai = lungimea celui mai scurt subsir crescator maximal care incepe cu pozitia i
- Ti = urmatorul element dupa pozitia i in cel mai scurt subsir crescator maximal care incepe cu i (pentru reconstiutire)
Pentru fiecare i, se va cauta un j > i astfel incat Vi ≤ Vj (unde V este vectorul de numere) si se alege acela cu Aj minim, Ai devenind Aj+1, iar Ti devine j. Daca nu exista nici un j, Ai se initializeaza cu 1 si Ti cu i.
Ca sirul construit sa fie maximal trebuie ca atunci cand verificam j-urile pentru un i fixat, j-ul respectiv sa fie "dominant", in sensul ca sa nu existe un i < k < j astfel incat Vi ≤ Vk ≤ Vj, deoarece sirul construit cu primul element in i si al doilea in j ar putea fi extins inserand k intre i si j. Verificarea pentru acest k se poate face in O(N), obtinand o solutie O(N3) care ar fi adus 50-60p. Pentru a face verificarea in O(1), facem observatia ca ne intereseaza doar acel Vk minim care este ≥ Vi. Pe masura ce se avanseaza cu variabila j, se pastreaza o variabila min, reprezentand minimul dintre valorile Vj parcurse pana acum, care sunt ≥ Vi.
Astfel, cand se ajunge la un j, se verifica inainte daca Vj < min (conditie necesara pentru a construi un sir maximal). Un ultim detaliu in solutie este obtinerea solutiei minime din punct de vedere lexicografic. Cand se selecteaza j-ul pentru fiecare i, pe langa faptul ca se alege acela cu Aj minim, in caz de egalitate se va alege acela cu valoarea Vj minima. Selectarea este corecta deoarece nu vor exista j1, j2 cu Aj1 si Aj2 minim , iar Vj1 = Vj2.
Problema se poate rezolva mai bine intr-o complexitate O(N*lg2 N) folosind structuri de date avansate, astfel transformandu-se intr-o problema de clasele 11-12 grea, sau chiar o problema de finala. Lasam aceasta rezolvare ca exercitiu pentru cititor.
Sum
(problema usoara, clasa a 10a)
Vom face o prima observatie:
- (n, d) = 1 <=> (n, n - d) = 1, (n, n + d) = 1
Fie a = phi (n), indicatorul lui Euler. Fie b numarul de numere prime cu n cuprinse intre n si 2 * n.
Deoarece (n, d) = 1 <=> (n, n + d) = 1, a ≤ b. Deoarece (n, d) = 1 <=> (n, n - d) = 1, b ≤ a => b = a. Fie x1, x2, .. xa numerele < n si prime cu n => numerele cuprinse intre n si 2 * n si prime cu n vor fi x1 + n, x2 + n, .. xa + n.
Conform observatiei facute, (n, n - x1) = 1, (n, n - x2) = 1, .. (n, n - xa) = 1 =>
xa = n - x1 <=> x1 + xa = n
xa-1 = n - x2 <=> x2 + xa-1 = n
...
x1 = n - xa <=> xa + x1 = n
Fie S1 suma numerelor prime cu n si mai mici ca n, fie S2 suma numerelor prime cu n, cuprinse intre n si 2 * n.
Adunand cele a egalitati, obtinem 2 * S1 = a * n => S1 = (a * n) / 2.
S2 = a * n + S1 => S1 + S2 = 2 * a * n.
Se foloseste o singura data ciurul lui Erathostene pentru a determina functia phi pentru toate intrebarile. Se poate consulta articolul despre cirulul lui Erathostene.
Pavare 2
(problema grea, clasa a 10a)
Problema se rezolva cu programare dinamica. Utilizam urmatoare structura de date:
- V[i][j][0] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie albe
- V[i][j][1] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie negre
Relatiile de recurenta sunt acum usor de dedus. Odata calculata matricea putem raspunde foarte usor primei cerinte, facand suma V[N][i][0] (pentru 1 ≤ i ≤ A) si V[N][i][1] pentru (1 ≤ i ≤ B).
Pentru a 2-a cerinta incercam sa construim a K-a secventa lexicografica de la inceput catre sfarsit. Astfel, la fiecare pas incercam sa punem o segventa de tipul '0...01' care sa contina un numar maxim de '0'. Daca la pasul curent nu putem pune nici un '0' atunci vom pune o secventa de tipul '1..1' care sa contina un numar minim de 1. Numarul de '0'-uri sau de '1' pe care il punem il vom calcula cu ajutorul matricei precalculate la prima cerinta. Astfel, daca putem pune p de '0' inseamna ca numarul de posibilitati pentru a completa restul solutiei daca punem cel putin p de '0' la inceput este mai mare sau egal cu K. Alegem cel mai mare numar p cu proprietatea de mai sus. Daca p nu exista, incercam sa punem cat mai putini '1' in aceeasi maniera. Continuam apoi cu restul secventei, iar din K scadem numarul de solutii peste care am "sarit".
Tare de tot acest sandbox :)
* Re: chiar ca e! poti sa te joci cu css aici :)
![\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &
\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &](http://www.infoarena.ro/static/images/latex/eef80f4248abc3249af6c045a561bf56_13.50015pt.gif)
scrieti "assert(fail)" la inceputul programului la olimpiada si merge de aprox. 10 ori mai rapid programu ca foloseste mai multe core-uri(merge in c++, dar si in c)
h1. KAKTUS
MULTE SMENURI DE PROGRAMARE IN C/C++... SI NU NUMAI!!!!!!!
Furnicuţa şi-a construit un depozit pentru grăunţe .pdf
oof
O zi frumoasa in cutiuţa cu năsip
Tudor Gălăţan a.k.a. How to be or not to be something.
<tex
| Ionescu | 12 | Constanta | Popescu | 24 | Bucuresti | Popescu | 24 | Bucuresti |
log me
LaTeX pe mai multe rânduri:
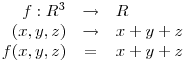
sau:
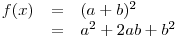
Tabel mic:d
| A | B | A->B |
| 0 | 2 | 3 |
Tabel mare:
| A | B | A->B |
| 1 | 2 | 3 |
Tabel si mai mare:
| A | B | A->B |
| 1 | 2 | 3 |
Diacritice:
Straşnic de îngâmfat, ţăranul crapă streaşina.
Straşnic de îngâmfat, ţăranul crapă streaşina.
In Windows XP sp2 cu IE6 fara update de font se vede asa:

Ordered list:
- 1st item
- 2nd item
Use only F/OSS, Microsft sucks ;) just because I say so.
Love Linux, beacuse I say so.
However, on a GNU system NEVER type <b>sudo make me sandwich</b> , and expect the results...
¡Entendido, amigo!
x
y
a weirdo put this text here
yey im playing with bleach
hi my name is cosine dabe ur frind dont tuch my gotye
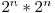
Vivi's blog
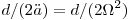
* 
p. 
Avem suport pentru  !
!
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
| test | test |
Worship me
Feel free to plghay around, but Big Brother is watching you.
What does this button do?
lalallaa
Intrebare: cum poti seta culoarea cu care scrii?
Uite asa: scris cu rosu
Siteul sub IE 7 -- vezi pagina dedicata
Siteul sub FF 2 - mica problema panoul de 'editeaza', 'vezi istoria', 'sterge' etc (in IE7 panoul nu se suprapune)

[test]
OMG test, good work people :D
Acuma doar trebuie putin stimulata comunitatea
[/test]
Interesting choice of words.
a very bold MAN
CAPSOMANII-I DESPISE THEM
gasise pe-un teren viran,
un geamantan.
si-n geamantan,
un pachet.
si in pachet,
un pachetel gasise el.
si-n pachetel,
alt pachetel.
si-un pachetel in pachetel,
legat cu funde elegante.
si-n pachetel...vreo 40 de diamante...
...
Adio voi...va las si plec fiindca mi-e dor...
si a plecat Apolodor
!!!<>
tralalala blablabla lala
salut, aici poate sa scrie oricine ce vrea? Robert
| 1 | 2 | 3 |
|---|---|---|
| unu | doi | trei |
| 1... unu | 2... doi | 3... trei |
Moraru Ionut has been here. :))
shnako was here :)
:) gosh...
inca unul, de tipul cel mai heyyyyyyyyyy prost din corcodus, se joaca cu in nisip.. ura ...
cel mai prost din corcodus a terminat... altcineva?:D
tot el: atentie fratilor ne urmareste big brother 3 (sau 4)
Care imi da o lopata ? :)
// comentariu
#include <cstdio> // comment1
// comment2
int main()
{
return 0;
}| Latura 1 | Latura 2 | Latura 3 | Latura 4 | Latura 2 | Latura 3 | Latura 1 |
|---|---|---|---|---|---|---|
| 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 |
&6 7 8&
# Hello
## Hello 2
### Hello 3

Subsir 2
(problema grea clasa a 9a, problema medie clasa a 10a, problema usoara clasele 11-12)
Problema poate fi considerata asemanatoare cu cea a celui mai lung subsir crescator, avand o rezolvare similara de complexitatea O(N2) folosind metoda programarii dinamice.
Se vor construi doi vectori:
- Ai = lungimea celui mai scurt subsir crescator maximal care incepe cu pozitia i
- Ti = urmatorul element dupa pozitia i in cel mai scurt subsir crescator maximal care incepe cu i (pentru reconstiutire)
Pentru fiecare i, se va cauta un j > i astfel incat Vi ≤ Vj (unde V este vectorul de numere) si se alege acela cu Aj minim, Ai devenind Aj+1, iar Ti devine j. Daca nu exista nici un j, Ai se initializeaza cu 1 si Ti cu i.
Ca sirul construit sa fie maximal trebuie ca atunci cand verificam j-urile pentru un i fixat, j-ul respectiv sa fie "dominant", in sensul ca sa nu existe un i < k < j astfel incat Vi ≤ Vk ≤ Vj, deoarece sirul construit cu primul element in i si al doilea in j ar putea fi extins inserand k intre i si j. Verificarea pentru acest k se poate face in O(N), obtinand o solutie O(N3) care ar fi adus 50-60p. Pentru a face verificarea in O(1), facem observatia ca ne intereseaza doar acel Vk minim care este ≥ Vi. Pe masura ce se avanseaza cu variabila j, se pastreaza o variabila min, reprezentand minimul dintre valorile Vj parcurse pana acum, care sunt ≥ Vi.
Astfel, cand se ajunge la un j, se verifica inainte daca Vj < min (conditie necesara pentru a construi un sir maximal). Un ultim detaliu in solutie este obtinerea solutiei minime din punct de vedere lexicografic. Cand se selecteaza j-ul pentru fiecare i, pe langa faptul ca se alege acela cu Aj minim, in caz de egalitate se va alege acela cu valoarea Vj minima. Selectarea este corecta deoarece nu vor exista j1, j2 cu Aj1 si Aj2 minim , iar Vj1 = Vj2.
Problema se poate rezolva mai bine intr-o complexitate O(N*lg2 N) folosind structuri de date avansate, astfel transformandu-se intr-o problema de clasele 11-12 grea, sau chiar o problema de finala. Lasam aceasta rezolvare ca exercitiu pentru cititor.
Sum
(problema usoara, clasa a 10a)
Vom face o prima observatie:
- (n, d) = 1 <=> (n, n - d) = 1, (n, n + d) = 1
Fie a = phi (n), indicatorul lui Euler. Fie b numarul de numere prime cu n cuprinse intre n si 2 * n.
Deoarece (n, d) = 1 <=> (n, n + d) = 1, a ≤ b. Deoarece (n, d) = 1 <=> (n, n - d) = 1, b ≤ a => b = a. Fie x1, x2, .. xa numerele < n si prime cu n => numerele cuprinse intre n si 2 * n si prime cu n vor fi x1 + n, x2 + n, .. xa + n.
Conform observatiei facute, (n, n - x1) = 1, (n, n - x2) = 1, .. (n, n - xa) = 1 =>
xa = n - x1 <=> x1 + xa = n
xa-1 = n - x2 <=> x2 + xa-1 = n
...
x1 = n - xa <=> xa + x1 = n
Fie S1 suma numerelor prime cu n si mai mici ca n, fie S2 suma numerelor prime cu n, cuprinse intre n si 2 * n.
Adunand cele a egalitati, obtinem 2 * S1 = a * n => S1 = (a * n) / 2.
S2 = a * n + S1 => S1 + S2 = 2 * a * n.
Se foloseste o singura data ciurul lui Erathostene pentru a determina functia phi pentru toate intrebarile. Se poate consulta articolul despre cirulul lui Erathostene.
Pavare 2
(problema grea, clasa a 10a)
Problema se rezolva cu programare dinamica. Utilizam urmatoare structura de date:
- V[i][j][0] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie albe
- V[i][j][1] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie negre
Relatiile de recurenta sunt acum usor de dedus. Odata calculata matricea putem raspunde foarte usor primei cerinte, facand suma V[N][i][0] (pentru 1 ≤ i ≤ A) si V[N][i][1] pentru (1 ≤ i ≤ B).
Pentru a 2-a cerinta incercam sa construim a K-a secventa lexicografica de la inceput catre sfarsit. Astfel, la fiecare pas incercam sa punem o segventa de tipul '0...01' care sa contina un numar maxim de '0'. Daca la pasul curent nu putem pune nici un '0' atunci vom pune o secventa de tipul '1..1' care sa contina un numar minim de 1. Numarul de '0'-uri sau de '1' pe care il punem il vom calcula cu ajutorul matricei precalculate la prima cerinta. Astfel, daca putem pune p de '0' inseamna ca numarul de posibilitati pentru a completa restul solutiei daca punem cel putin p de '0' la inceput este mai mare sau egal cu K. Alegem cel mai mare numar p cu proprietatea de mai sus. Daca p nu exista, incercam sa punem cat mai putini '1' in aceeasi maniera. Continuam apoi cu restul secventei, iar din K scadem numarul de solutii peste care am "sarit".
Tare de tot acest sandbox :)
* Re: chiar ca e! poti sa te joci cu css aici :)
![\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &
\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &](http://www.infoarena.ro/static/images/latex/eef80f4248abc3249af6c045a561bf56_13.50015pt.gif)
scrieti "assert(fail)" la inceputul programului la olimpiada si merge de aprox. 10 ori mai rapid programu ca foloseste mai multe core-uri(merge in c++, dar si in c)
h1. KAKTUS
MULTE SMENURI DE PROGRAMARE IN C/C++... SI NU NUMAI!!!!!!!
Furnicuţa şi-a construit un depozit pentru grăunţe .pdf
oof
O zi frumoasa in cutiuţa cu năsip
Tudor Gălăţan a.k.a. How to be or not to be something.
<tex
| Ionescu | 12 | Constanta | Popescu | 24 | Bucuresti | Popescu | 24 | Bucuresti |
log me
LaTeX pe mai multe rânduri:
sau:
Tabel mic:d
| A | B | A->B |
| 0 | 2 | 3 |
Tabel mare:
| A | B | A->B |
| 1 | 2 | 3 |
Tabel si mai mare:
| A | B | A->B |
| 1 | 2 | 3 |
Diacritice:
Straşnic de îngâmfat, ţăranul crapă streaşina.
Straşnic de îngâmfat, ţăranul crapă streaşina.
In Windows XP sp2 cu IE6 fara update de font se vede asa:

Ordered list:
- 1st item
- 2nd item
Use only F/OSS, Microsft sucks ;) just because I say so.
Love Linux, beacuse I say so.
However, on a GNU system NEVER type <b>sudo make me sandwich</b> , and expect the results...
¡Entendido, amigo!
x
y
a weirdo put this text here
yey im playing with bleach
hi my name is cosine dabe ur frind dont tuch my gotye
Vivi's blog
* 
p. 
Avem suport pentru  !
!
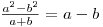
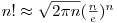
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
| test | test |
Worship me
Feel free to plghay around, but Big Brother is watching you.
What does this button do?
lalallaa
Intrebare: cum poti seta culoarea cu care scrii?
Uite asa: scris cu rosu
Siteul sub IE 7 -- vezi pagina dedicata
Siteul sub FF 2 - mica problema panoul de 'editeaza', 'vezi istoria', 'sterge' etc (in IE7 panoul nu se suprapune)

[test]
OMG test, good work people :D
Acuma doar trebuie putin stimulata comunitatea
[/test]
Interesting choice of words.
a very bold MAN
CAPSOMANII-I DESPISE THEM
gasise pe-un teren viran,
un geamantan.
si-n geamantan,
un pachet.
si in pachet,
un pachetel gasise el.
si-n pachetel,
alt pachetel.
si-un pachetel in pachetel,
legat cu funde elegante.
si-n pachetel...vreo 40 de diamante...
...
Adio voi...va las si plec fiindca mi-e dor...
si a plecat Apolodor
!!!<>
tralalala blablabla lala
salut, aici poate sa scrie oricine ce vrea? Robert
| 1 | 2 | 3 |
|---|---|---|
| unu | doi | trei |
| 1... unu | 2... doi | 3... trei |
Moraru Ionut has been here. :))
shnako was here :)
:) gosh...
inca unul, de tipul cel mai heyyyyyyyyyy prost din corcodus, se joaca cu in nisip.. ura ...
cel mai prost din corcodus a terminat... altcineva?:D
tot el: atentie fratilor ne urmareste big brother 3 (sau 4)
Care imi da o lopata ? :)
// comentariu
#include <cstdio> // comment1
// comment2
int main()
{
return 0;
}| Latura 1 | Latura 2 | Latura 3 | Latura 4 | Latura 2 | Latura 3 | Latura 1 |
|---|---|---|---|---|---|---|
| 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 |
&6 7 8&
# Hello
## Hello 2
### Hello 3

Subsir 2
(problema grea clasa a 9a, problema medie clasa a 10a, problema usoara clasele 11-12)
Problema poate fi considerata asemanatoare cu cea a celui mai lung subsir crescator, avand o rezolvare similara de complexitatea O(N2) folosind metoda programarii dinamice.
Se vor construi doi vectori:
- Ai = lungimea celui mai scurt subsir crescator maximal care incepe cu pozitia i
- Ti = urmatorul element dupa pozitia i in cel mai scurt subsir crescator maximal care incepe cu i (pentru reconstiutire)
Pentru fiecare i, se va cauta un j > i astfel incat Vi ≤ Vj (unde V este vectorul de numere) si se alege acela cu Aj minim, Ai devenind Aj+1, iar Ti devine j. Daca nu exista nici un j, Ai se initializeaza cu 1 si Ti cu i.
Ca sirul construit sa fie maximal trebuie ca atunci cand verificam j-urile pentru un i fixat, j-ul respectiv sa fie "dominant", in sensul ca sa nu existe un i < k < j astfel incat Vi ≤ Vk ≤ Vj, deoarece sirul construit cu primul element in i si al doilea in j ar putea fi extins inserand k intre i si j. Verificarea pentru acest k se poate face in O(N), obtinand o solutie O(N3) care ar fi adus 50-60p. Pentru a face verificarea in O(1), facem observatia ca ne intereseaza doar acel Vk minim care este ≥ Vi. Pe masura ce se avanseaza cu variabila j, se pastreaza o variabila min, reprezentand minimul dintre valorile Vj parcurse pana acum, care sunt ≥ Vi.
Astfel, cand se ajunge la un j, se verifica inainte daca Vj < min (conditie necesara pentru a construi un sir maximal). Un ultim detaliu in solutie este obtinerea solutiei minime din punct de vedere lexicografic. Cand se selecteaza j-ul pentru fiecare i, pe langa faptul ca se alege acela cu Aj minim, in caz de egalitate se va alege acela cu valoarea Vj minima. Selectarea este corecta deoarece nu vor exista j1, j2 cu Aj1 si Aj2 minim , iar Vj1 = Vj2.
Problema se poate rezolva mai bine intr-o complexitate O(N*lg2 N) folosind structuri de date avansate, astfel transformandu-se intr-o problema de clasele 11-12 grea, sau chiar o problema de finala. Lasam aceasta rezolvare ca exercitiu pentru cititor.
Sum
(problema usoara, clasa a 10a)
Vom face o prima observatie:
- (n, d) = 1 <=> (n, n - d) = 1, (n, n + d) = 1
Fie a = phi (n), indicatorul lui Euler. Fie b numarul de numere prime cu n cuprinse intre n si 2 * n.
Deoarece (n, d) = 1 <=> (n, n + d) = 1, a ≤ b. Deoarece (n, d) = 1 <=> (n, n - d) = 1, b ≤ a => b = a. Fie x1, x2, .. xa numerele < n si prime cu n => numerele cuprinse intre n si 2 * n si prime cu n vor fi x1 + n, x2 + n, .. xa + n.
Conform observatiei facute, (n, n - x1) = 1, (n, n - x2) = 1, .. (n, n - xa) = 1 =>
xa = n - x1 <=> x1 + xa = n
xa-1 = n - x2 <=> x2 + xa-1 = n
...
x1 = n - xa <=> xa + x1 = n
Fie S1 suma numerelor prime cu n si mai mici ca n, fie S2 suma numerelor prime cu n, cuprinse intre n si 2 * n.
Adunand cele a egalitati, obtinem 2 * S1 = a * n => S1 = (a * n) / 2.
S2 = a * n + S1 => S1 + S2 = 2 * a * n.
Se foloseste o singura data ciurul lui Erathostene pentru a determina functia phi pentru toate intrebarile. Se poate consulta articolul despre cirulul lui Erathostene.
Pavare 2
(problema grea, clasa a 10a)
Problema se rezolva cu programare dinamica. Utilizam urmatoare structura de date:
- V[i][j][0] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie albe
- V[i][j][1] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie negre
Relatiile de recurenta sunt acum usor de dedus. Odata calculata matricea putem raspunde foarte usor primei cerinte, facand suma V[N][i][0] (pentru 1 ≤ i ≤ A) si V[N][i][1] pentru (1 ≤ i ≤ B).
Pentru a 2-a cerinta incercam sa construim a K-a secventa lexicografica de la inceput catre sfarsit. Astfel, la fiecare pas incercam sa punem o segventa de tipul '0...01' care sa contina un numar maxim de '0'. Daca la pasul curent nu putem pune nici un '0' atunci vom pune o secventa de tipul '1..1' care sa contina un numar minim de 1. Numarul de '0'-uri sau de '1' pe care il punem il vom calcula cu ajutorul matricei precalculate la prima cerinta. Astfel, daca putem pune p de '0' inseamna ca numarul de posibilitati pentru a completa restul solutiei daca punem cel putin p de '0' la inceput este mai mare sau egal cu K. Alegem cel mai mare numar p cu proprietatea de mai sus. Daca p nu exista, incercam sa punem cat mai putini '1' in aceeasi maniera. Continuam apoi cu restul secventei, iar din K scadem numarul de solutii peste care am "sarit".
Tare de tot acest sandbox :)
* Re: chiar ca e! poti sa te joci cu css aici :)
![\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &
\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &](http://www.infoarena.ro/static/images/latex/eef80f4248abc3249af6c045a561bf56_13.50015pt.gif)
scrieti "assert(fail)" la inceputul programului la olimpiada si merge de aprox. 10 ori mai rapid programu ca foloseste mai multe core-uri(merge in c++, dar si in c)
h1. KAKTUS
MULTE SMENURI DE PROGRAMARE IN C/C++... SI NU NUMAI!!!!!!!
Furnicuţa şi-a construit un depozit pentru grăunţe .pdf
oof
O zi frumoasa in cutiuţa cu năsip
Tudor Gălăţan a.k.a. How to be or not to be something.
<tex
| Ionescu | 12 | Constanta | Popescu | 24 | Bucuresti | Popescu | 24 | Bucuresti |
log me
LaTeX pe mai multe rânduri:
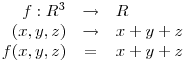
sau:
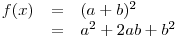
Tabel mic:d
| A | B | A->B |
| 0 | 2 | 3 |
Tabel mare:
| A | B | A->B |
| 1 | 2 | 3 |
Tabel si mai mare:
| A | B | A->B |
| 1 | 2 | 3 |
Diacritice:
Straşnic de îngâmfat, ţăranul crapă streaşina.
Straşnic de îngâmfat, ţăranul crapă streaşina.
In Windows XP sp2 cu IE6 fara update de font se vede asa:

Ordered list:
- 1st item
- 2nd item
Use only F/OSS, Microsft sucks ;) just because I say so.
Love Linux, beacuse I say so.
However, on a GNU system NEVER type <b>sudo make me sandwich</b> , and expect the results...
¡Entendido, amigo!
x
y
a weirdo put this text here
yey im playing with bleach
hi my name is cosine dabe ur frind dont tuch my gotye
Vivi's blog
* 
p. 
Avem suport pentru  !
!
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
| test | test |
Worship me
Feel free to plghay around, but Big Brother is watching you.
What does this button do?
lalallaa
Intrebare: cum poti seta culoarea cu care scrii?
Uite asa: scris cu rosu
Siteul sub IE 7 -- vezi pagina dedicata
Siteul sub FF 2 - mica problema panoul de 'editeaza', 'vezi istoria', 'sterge' etc (in IE7 panoul nu se suprapune)

[test]
OMG test, good work people :D
Acuma doar trebuie putin stimulata comunitatea
[/test]
Interesting choice of words.
a very bold MAN
CAPSOMANII-I DESPISE THEM
gasise pe-un teren viran,
un geamantan.
si-n geamantan,
un pachet.
si in pachet,
un pachetel gasise el.
si-n pachetel,
alt pachetel.
si-un pachetel in pachetel,
legat cu funde elegante.
si-n pachetel...vreo 40 de diamante...
...
Adio voi...va las si plec fiindca mi-e dor...
si a plecat Apolodor
!!!<>
tralalala blablabla lala
salut, aici poate sa scrie oricine ce vrea? Robert
| 1 | 2 | 3 |
|---|---|---|
| unu | doi | trei |
| 1... unu | 2... doi | 3... trei |
Moraru Ionut has been here. :))
shnako was here :)
:) gosh...
inca unul, de tipul cel mai heyyyyyyyyyy prost din corcodus, se joaca cu in nisip.. ura ...
cel mai prost din corcodus a terminat... altcineva?:D
tot el: atentie fratilor ne urmareste big brother 3 (sau 4)
Care imi da o lopata ? :)
// comentariu
#include <cstdio> // comment1
// comment2
int main()
{
return 0;
}| Latura 1 | Latura 2 | Latura 3 | Latura 4 | Latura 2 | Latura 3 | Latura 1 |
|---|---|---|---|---|---|---|
| 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 |
&6 7 8&
# Hello
## Hello 2
### Hello 3

Subsir 2
(problema grea clasa a 9a, problema medie clasa a 10a, problema usoara clasele 11-12)
Problema poate fi considerata asemanatoare cu cea a celui mai lung subsir crescator, avand o rezolvare similara de complexitatea O(N2) folosind metoda programarii dinamice.
Se vor construi doi vectori:
- Ai = lungimea celui mai scurt subsir crescator maximal care incepe cu pozitia i
- Ti = urmatorul element dupa pozitia i in cel mai scurt subsir crescator maximal care incepe cu i (pentru reconstiutire)
Pentru fiecare i, se va cauta un j > i astfel incat Vi ≤ Vj (unde V este vectorul de numere) si se alege acela cu Aj minim, Ai devenind Aj+1, iar Ti devine j. Daca nu exista nici un j, Ai se initializeaza cu 1 si Ti cu i.
Ca sirul construit sa fie maximal trebuie ca atunci cand verificam j-urile pentru un i fixat, j-ul respectiv sa fie "dominant", in sensul ca sa nu existe un i < k < j astfel incat Vi ≤ Vk ≤ Vj, deoarece sirul construit cu primul element in i si al doilea in j ar putea fi extins inserand k intre i si j. Verificarea pentru acest k se poate face in O(N), obtinand o solutie O(N3) care ar fi adus 50-60p. Pentru a face verificarea in O(1), facem observatia ca ne intereseaza doar acel Vk minim care este ≥ Vi. Pe masura ce se avanseaza cu variabila j, se pastreaza o variabila min, reprezentand minimul dintre valorile Vj parcurse pana acum, care sunt ≥ Vi.
Astfel, cand se ajunge la un j, se verifica inainte daca Vj < min (conditie necesara pentru a construi un sir maximal). Un ultim detaliu in solutie este obtinerea solutiei minime din punct de vedere lexicografic. Cand se selecteaza j-ul pentru fiecare i, pe langa faptul ca se alege acela cu Aj minim, in caz de egalitate se va alege acela cu valoarea Vj minima. Selectarea este corecta deoarece nu vor exista j1, j2 cu Aj1 si Aj2 minim , iar Vj1 = Vj2.
Problema se poate rezolva mai bine intr-o complexitate O(N*lg2 N) folosind structuri de date avansate, astfel transformandu-se intr-o problema de clasele 11-12 grea, sau chiar o problema de finala. Lasam aceasta rezolvare ca exercitiu pentru cititor.
Sum
(problema usoara, clasa a 10a)
Vom face o prima observatie:
- (n, d) = 1 <=> (n, n - d) = 1, (n, n + d) = 1
Fie a = phi (n), indicatorul lui Euler. Fie b numarul de numere prime cu n cuprinse intre n si 2 * n.
Deoarece (n, d) = 1 <=> (n, n + d) = 1, a ≤ b. Deoarece (n, d) = 1 <=> (n, n - d) = 1, b ≤ a => b = a. Fie x1, x2, .. xa numerele < n si prime cu n => numerele cuprinse intre n si 2 * n si prime cu n vor fi x1 + n, x2 + n, .. xa + n.
Conform observatiei facute, (n, n - x1) = 1, (n, n - x2) = 1, .. (n, n - xa) = 1 =>
xa = n - x1 <=> x1 + xa = n
xa-1 = n - x2 <=> x2 + xa-1 = n
...
x1 = n - xa <=> xa + x1 = n
Fie S1 suma numerelor prime cu n si mai mici ca n, fie S2 suma numerelor prime cu n, cuprinse intre n si 2 * n.
Adunand cele a egalitati, obtinem 2 * S1 = a * n => S1 = (a * n) / 2.
S2 = a * n + S1 => S1 + S2 = 2 * a * n.
Se foloseste o singura data ciurul lui Erathostene pentru a determina functia phi pentru toate intrebarile. Se poate consulta articolul despre cirulul lui Erathostene.
Pavare 2
(problema grea, clasa a 10a)
Problema se rezolva cu programare dinamica. Utilizam urmatoare structura de date:
- V[i][j][0] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie albe
- V[i][j][1] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie negre
Relatiile de recurenta sunt acum usor de dedus. Odata calculata matricea putem raspunde foarte usor primei cerinte, facand suma V[N][i][0] (pentru 1 ≤ i ≤ A) si V[N][i][1] pentru (1 ≤ i ≤ B).
Pentru a 2-a cerinta incercam sa construim a K-a secventa lexicografica de la inceput catre sfarsit. Astfel, la fiecare pas incercam sa punem o segventa de tipul '0...01' care sa contina un numar maxim de '0'. Daca la pasul curent nu putem pune nici un '0' atunci vom pune o secventa de tipul '1..1' care sa contina un numar minim de 1. Numarul de '0'-uri sau de '1' pe care il punem il vom calcula cu ajutorul matricei precalculate la prima cerinta. Astfel, daca putem pune p de '0' inseamna ca numarul de posibilitati pentru a completa restul solutiei daca punem cel putin p de '0' la inceput este mai mare sau egal cu K. Alegem cel mai mare numar p cu proprietatea de mai sus. Daca p nu exista, incercam sa punem cat mai putini '1' in aceeasi maniera. Continuam apoi cu restul secventei, iar din K scadem numarul de solutii peste care am "sarit".
Tare de tot acest sandbox :)
* Re: chiar ca e! poti sa te joci cu css aici :)
![\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &
\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &](http://www.infoarena.ro/static/images/latex/eef80f4248abc3249af6c045a561bf56_13.50015pt.gif)
scrieti "assert(fail)" la inceputul programului la olimpiada si merge de aprox. 10 ori mai rapid programu ca foloseste mai multe core-uri(merge in c++, dar si in c)
h1. KAKTUS
MULTE SMENURI DE PROGRAMARE IN C/C++... SI NU NUMAI!!!!!!!
Furnicuţa şi-a construit un depozit pentru grăunţe .pdf
oof
O zi frumoasa in cutiuţa cu năsip
Tudor Gălăţan a.k.a. How to be or not to be something.
<tex
| Ionescu | 12 | Constanta | Popescu | 24 | Bucuresti | Popescu | 24 | Bucuresti |
log me
LaTeX pe mai multe rânduri:
sau:
Tabel mic:d
| A | B | A->B |
| 0 | 2 | 3 |
Tabel mare:
| A | B | A->B |
| 1 | 2 | 3 |
Tabel si mai mare:
| A | B | A->B |
| 1 | 2 | 3 |
Diacritice:
Straşnic de îngâmfat, ţăranul crapă streaşina.
Straşnic de îngâmfat, ţăranul crapă streaşina.
In Windows XP sp2 cu IE6 fara update de font se vede asa:

Ordered list:
- 1st item
- 2nd item
Use only F/OSS, Microsft sucks ;) just because I say so.
Love Linux, beacuse I say so.
However, on a GNU system NEVER type <b>sudo make me sandwich</b> , and expect the results...
¡Entendido, amigo!
x
y
a weirdo put this text here
yey im playing with bleach
hi my name is cosine dabe ur frind dont tuch my gotye
Vivi's blog
* 
p. 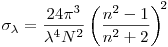
Avem suport pentru 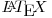 !
!
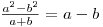
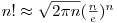
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
| test | test |
Worship me
Feel free to plghay around, but Big Brother is watching you.
What does this button do?
lalallaa
Intrebare: cum poti seta culoarea cu care scrii?
Uite asa: scris cu rosu
Siteul sub IE 7 -- vezi pagina dedicata
Siteul sub FF 2 - mica problema panoul de 'editeaza', 'vezi istoria', 'sterge' etc (in IE7 panoul nu se suprapune)

[test]
OMG test, good work people :D
Acuma doar trebuie putin stimulata comunitatea
[/test]
Interesting choice of words.
a very bold MAN
CAPSOMANII-I DESPISE THEM
gasise pe-un teren viran,
un geamantan.
si-n geamantan,
un pachet.
si in pachet,
un pachetel gasise el.
si-n pachetel,
alt pachetel.
si-un pachetel in pachetel,
legat cu funde elegante.
si-n pachetel...vreo 40 de diamante...
...
Adio voi...va las si plec fiindca mi-e dor...
si a plecat Apolodor
!!!<>
tralalala blablabla lala
salut, aici poate sa scrie oricine ce vrea? Robert
| 1 | 2 | 3 |
|---|---|---|
| unu | doi | trei |
| 1... unu | 2... doi | 3... trei |
Moraru Ionut has been here. :))
shnako was here :)
:) gosh...
inca unul, de tipul cel mai heyyyyyyyyyy prost din corcodus, se joaca cu in nisip.. ura ...
cel mai prost din corcodus a terminat... altcineva?:D
tot el: atentie fratilor ne urmareste big brother 3 (sau 4)
Care imi da o lopata ? :)
// comentariu
#include <cstdio> // comment1
// comment2
int main()
{
return 0;
}| Latura 1 | Latura 2 | Latura 3 | Latura 4 | Latura 2 | Latura 3 | Latura 1 |
|---|---|---|---|---|---|---|
| 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 |
&6 7 8&
# Hello
## Hello 2
### Hello 3

Subsir 2
(problema grea clasa a 9a, problema medie clasa a 10a, problema usoara clasele 11-12)
Problema poate fi considerata asemanatoare cu cea a celui mai lung subsir crescator, avand o rezolvare similara de complexitatea O(N2) folosind metoda programarii dinamice.
Se vor construi doi vectori:
- Ai = lungimea celui mai scurt subsir crescator maximal care incepe cu pozitia i
- Ti = urmatorul element dupa pozitia i in cel mai scurt subsir crescator maximal care incepe cu i (pentru reconstiutire)
Pentru fiecare i, se va cauta un j > i astfel incat Vi ≤ Vj (unde V este vectorul de numere) si se alege acela cu Aj minim, Ai devenind Aj+1, iar Ti devine j. Daca nu exista nici un j, Ai se initializeaza cu 1 si Ti cu i.
Ca sirul construit sa fie maximal trebuie ca atunci cand verificam j-urile pentru un i fixat, j-ul respectiv sa fie "dominant", in sensul ca sa nu existe un i < k < j astfel incat Vi ≤ Vk ≤ Vj, deoarece sirul construit cu primul element in i si al doilea in j ar putea fi extins inserand k intre i si j. Verificarea pentru acest k se poate face in O(N), obtinand o solutie O(N3) care ar fi adus 50-60p. Pentru a face verificarea in O(1), facem observatia ca ne intereseaza doar acel Vk minim care este ≥ Vi. Pe masura ce se avanseaza cu variabila j, se pastreaza o variabila min, reprezentand minimul dintre valorile Vj parcurse pana acum, care sunt ≥ Vi.
Astfel, cand se ajunge la un j, se verifica inainte daca Vj < min (conditie necesara pentru a construi un sir maximal). Un ultim detaliu in solutie este obtinerea solutiei minime din punct de vedere lexicografic. Cand se selecteaza j-ul pentru fiecare i, pe langa faptul ca se alege acela cu Aj minim, in caz de egalitate se va alege acela cu valoarea Vj minima. Selectarea este corecta deoarece nu vor exista j1, j2 cu Aj1 si Aj2 minim , iar Vj1 = Vj2.
Problema se poate rezolva mai bine intr-o complexitate O(N*lg2 N) folosind structuri de date avansate, astfel transformandu-se intr-o problema de clasele 11-12 grea, sau chiar o problema de finala. Lasam aceasta rezolvare ca exercitiu pentru cititor.
Sum
(problema usoara, clasa a 10a)
Vom face o prima observatie:
- (n, d) = 1 <=> (n, n - d) = 1, (n, n + d) = 1
Fie a = phi (n), indicatorul lui Euler. Fie b numarul de numere prime cu n cuprinse intre n si 2 * n.
Deoarece (n, d) = 1 <=> (n, n + d) = 1, a ≤ b. Deoarece (n, d) = 1 <=> (n, n - d) = 1, b ≤ a => b = a. Fie x1, x2, .. xa numerele < n si prime cu n => numerele cuprinse intre n si 2 * n si prime cu n vor fi x1 + n, x2 + n, .. xa + n.
Conform observatiei facute, (n, n - x1) = 1, (n, n - x2) = 1, .. (n, n - xa) = 1 =>
xa = n - x1 <=> x1 + xa = n
xa-1 = n - x2 <=> x2 + xa-1 = n
...
x1 = n - xa <=> xa + x1 = n
Fie S1 suma numerelor prime cu n si mai mici ca n, fie S2 suma numerelor prime cu n, cuprinse intre n si 2 * n.
Adunand cele a egalitati, obtinem 2 * S1 = a * n => S1 = (a * n) / 2.
S2 = a * n + S1 => S1 + S2 = 2 * a * n.
Se foloseste o singura data ciurul lui Erathostene pentru a determina functia phi pentru toate intrebarile. Se poate consulta articolul despre cirulul lui Erathostene.
Pavare 2
(problema grea, clasa a 10a)
Problema se rezolva cu programare dinamica. Utilizam urmatoare structura de date:
- V[i][j][0] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie albe
- V[i][j][1] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie negre
Relatiile de recurenta sunt acum usor de dedus. Odata calculata matricea putem raspunde foarte usor primei cerinte, facand suma V[N][i][0] (pentru 1 ≤ i ≤ A) si V[N][i][1] pentru (1 ≤ i ≤ B).
Pentru a 2-a cerinta incercam sa construim a K-a secventa lexicografica de la inceput catre sfarsit. Astfel, la fiecare pas incercam sa punem o segventa de tipul '0...01' care sa contina un numar maxim de '0'. Daca la pasul curent nu putem pune nici un '0' atunci vom pune o secventa de tipul '1..1' care sa contina un numar minim de 1. Numarul de '0'-uri sau de '1' pe care il punem il vom calcula cu ajutorul matricei precalculate la prima cerinta. Astfel, daca putem pune p de '0' inseamna ca numarul de posibilitati pentru a completa restul solutiei daca punem cel putin p de '0' la inceput este mai mare sau egal cu K. Alegem cel mai mare numar p cu proprietatea de mai sus. Daca p nu exista, incercam sa punem cat mai putini '1' in aceeasi maniera. Continuam apoi cu restul secventei, iar din K scadem numarul de solutii peste care am "sarit".
Tare de tot acest sandbox :)
* Re: chiar ca e! poti sa te joci cu css aici :)
![\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &
\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &](http://www.infoarena.ro/static/images/latex/eef80f4248abc3249af6c045a561bf56_13.50015pt.gif)
scrieti "assert(fail)" la inceputul programului la olimpiada si merge de aprox. 10 ori mai rapid programu ca foloseste mai multe core-uri(merge in c++, dar si in c)
h1. KAKTUS
MULTE SMENURI DE PROGRAMARE IN C/C++... SI NU NUMAI!!!!!!!
Furnicuţa şi-a construit un depozit pentru grăunţe .pdf
oof
O zi frumoasa in cutiuţa cu năsip
Tudor Gălăţan a.k.a. How to be or not to be something.
<tex
| Ionescu | 12 | Constanta | Popescu | 24 | Bucuresti | Popescu | 24 | Bucuresti |
log me
LaTeX pe mai multe rânduri:
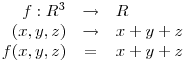
sau:
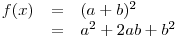
Tabel mic:d
| A | B | A->B |
| 0 | 2 | 3 |
Tabel mare:
| A | B | A->B |
| 1 | 2 | 3 |
Tabel si mai mare:
| A | B | A->B |
| 1 | 2 | 3 |
Diacritice:
Straşnic de îngâmfat, ţăranul crapă streaşina.
Straşnic de îngâmfat, ţăranul crapă streaşina.
In Windows XP sp2 cu IE6 fara update de font se vede asa:

Ordered list:
- 1st item
- 2nd item
Use only F/OSS, Microsft sucks ;) just because I say so.
Love Linux, beacuse I say so.
However, on a GNU system NEVER type <b>sudo make me sandwich</b> , and expect the results...
¡Entendido, amigo!
x
y
a weirdo put this text here
yey im playing with bleach
hi my name is cosine dabe ur frind dont tuch my gotye
Vivi's blog
* 
p. 
Avem suport pentru  !
!
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
| test | test |
Worship me
Feel free to plghay around, but Big Brother is watching you.
What does this button do?
lalallaa
Intrebare: cum poti seta culoarea cu care scrii?
Uite asa: scris cu rosu
Siteul sub IE 7 -- vezi pagina dedicata
Siteul sub FF 2 - mica problema panoul de 'editeaza', 'vezi istoria', 'sterge' etc (in IE7 panoul nu se suprapune)

[test]
OMG test, good work people :D
Acuma doar trebuie putin stimulata comunitatea
[/test]
Interesting choice of words.
a very bold MAN
CAPSOMANII-I DESPISE THEM
gasise pe-un teren viran,
un geamantan.
si-n geamantan,
un pachet.
si in pachet,
un pachetel gasise el.
si-n pachetel,
alt pachetel.
si-un pachetel in pachetel,
legat cu funde elegante.
si-n pachetel...vreo 40 de diamante...
...
Adio voi...va las si plec fiindca mi-e dor...
si a plecat Apolodor
!!!<>
tralalala blablabla lala
salut, aici poate sa scrie oricine ce vrea? Robert
| 1 | 2 | 3 |
|---|---|---|
| unu | doi | trei |
| 1... unu | 2... doi | 3... trei |
Moraru Ionut has been here. :))
shnako was here :)
:) gosh...
inca unul, de tipul cel mai heyyyyyyyyyy prost din corcodus, se joaca cu in nisip.. ura ...
cel mai prost din corcodus a terminat... altcineva?:D
tot el: atentie fratilor ne urmareste big brother 3 (sau 4)
Care imi da o lopata ? :)
// comentariu
#include <cstdio> // comment1
// comment2
int main()
{
return 0;
}| Latura 1 | Latura 2 | Latura 3 | Latura 4 | Latura 2 | Latura 3 | Latura 1 |
|---|---|---|---|---|---|---|
| 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 |
&6 7 8&
# Hello
## Hello 2
### Hello 3

Subsir 2
(problema grea clasa a 9a, problema medie clasa a 10a, problema usoara clasele 11-12)
Problema poate fi considerata asemanatoare cu cea a celui mai lung subsir crescator, avand o rezolvare similara de complexitatea O(N2) folosind metoda programarii dinamice.
Se vor construi doi vectori:
- Ai = lungimea celui mai scurt subsir crescator maximal care incepe cu pozitia i
- Ti = urmatorul element dupa pozitia i in cel mai scurt subsir crescator maximal care incepe cu i (pentru reconstiutire)
Pentru fiecare i, se va cauta un j > i astfel incat Vi ≤ Vj (unde V este vectorul de numere) si se alege acela cu Aj minim, Ai devenind Aj+1, iar Ti devine j. Daca nu exista nici un j, Ai se initializeaza cu 1 si Ti cu i.
Ca sirul construit sa fie maximal trebuie ca atunci cand verificam j-urile pentru un i fixat, j-ul respectiv sa fie "dominant", in sensul ca sa nu existe un i < k < j astfel incat Vi ≤ Vk ≤ Vj, deoarece sirul construit cu primul element in i si al doilea in j ar putea fi extins inserand k intre i si j. Verificarea pentru acest k se poate face in O(N), obtinand o solutie O(N3) care ar fi adus 50-60p. Pentru a face verificarea in O(1), facem observatia ca ne intereseaza doar acel Vk minim care este ≥ Vi. Pe masura ce se avanseaza cu variabila j, se pastreaza o variabila min, reprezentand minimul dintre valorile Vj parcurse pana acum, care sunt ≥ Vi.
Astfel, cand se ajunge la un j, se verifica inainte daca Vj < min (conditie necesara pentru a construi un sir maximal). Un ultim detaliu in solutie este obtinerea solutiei minime din punct de vedere lexicografic. Cand se selecteaza j-ul pentru fiecare i, pe langa faptul ca se alege acela cu Aj minim, in caz de egalitate se va alege acela cu valoarea Vj minima. Selectarea este corecta deoarece nu vor exista j1, j2 cu Aj1 si Aj2 minim , iar Vj1 = Vj2.
Problema se poate rezolva mai bine intr-o complexitate O(N*lg2 N) folosind structuri de date avansate, astfel transformandu-se intr-o problema de clasele 11-12 grea, sau chiar o problema de finala. Lasam aceasta rezolvare ca exercitiu pentru cititor.
Sum
(problema usoara, clasa a 10a)
Vom face o prima observatie:
- (n, d) = 1 <=> (n, n - d) = 1, (n, n + d) = 1
Fie a = phi (n), indicatorul lui Euler. Fie b numarul de numere prime cu n cuprinse intre n si 2 * n.
Deoarece (n, d) = 1 <=> (n, n + d) = 1, a ≤ b. Deoarece (n, d) = 1 <=> (n, n - d) = 1, b ≤ a => b = a. Fie x1, x2, .. xa numerele < n si prime cu n => numerele cuprinse intre n si 2 * n si prime cu n vor fi x1 + n, x2 + n, .. xa + n.
Conform observatiei facute, (n, n - x1) = 1, (n, n - x2) = 1, .. (n, n - xa) = 1 =>
xa = n - x1 <=> x1 + xa = n
xa-1 = n - x2 <=> x2 + xa-1 = n
...
x1 = n - xa <=> xa + x1 = n
Fie S1 suma numerelor prime cu n si mai mici ca n, fie S2 suma numerelor prime cu n, cuprinse intre n si 2 * n.
Adunand cele a egalitati, obtinem 2 * S1 = a * n => S1 = (a * n) / 2.
S2 = a * n + S1 => S1 + S2 = 2 * a * n.
Se foloseste o singura data ciurul lui Erathostene pentru a determina functia phi pentru toate intrebarile. Se poate consulta articolul despre cirulul lui Erathostene.
Pavare 2
(problema grea, clasa a 10a)
Problema se rezolva cu programare dinamica. Utilizam urmatoare structura de date:
- V[i][j][0] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie albe
- V[i][j][1] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie negre
Relatiile de recurenta sunt acum usor de dedus. Odata calculata matricea putem raspunde foarte usor primei cerinte, facand suma V[N][i][0] (pentru 1 ≤ i ≤ A) si V[N][i][1] pentru (1 ≤ i ≤ B).
Pentru a 2-a cerinta incercam sa construim a K-a secventa lexicografica de la inceput catre sfarsit. Astfel, la fiecare pas incercam sa punem o segventa de tipul '0...01' care sa contina un numar maxim de '0'. Daca la pasul curent nu putem pune nici un '0' atunci vom pune o secventa de tipul '1..1' care sa contina un numar minim de 1. Numarul de '0'-uri sau de '1' pe care il punem il vom calcula cu ajutorul matricei precalculate la prima cerinta. Astfel, daca putem pune p de '0' inseamna ca numarul de posibilitati pentru a completa restul solutiei daca punem cel putin p de '0' la inceput este mai mare sau egal cu K. Alegem cel mai mare numar p cu proprietatea de mai sus. Daca p nu exista, incercam sa punem cat mai putini '1' in aceeasi maniera. Continuam apoi cu restul secventei, iar din K scadem numarul de solutii peste care am "sarit".
Tare de tot acest sandbox :)
* Re: chiar ca e! poti sa te joci cu css aici :)
![\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &
\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &](http://www.infoarena.ro/static/images/latex/eef80f4248abc3249af6c045a561bf56_13.50015pt.gif)
scrieti "assert(fail)" la inceputul programului la olimpiada si merge de aprox. 10 ori mai rapid programu ca foloseste mai multe core-uri(merge in c++, dar si in c)
h1. KAKTUS
MULTE SMENURI DE PROGRAMARE IN C/C++... SI NU NUMAI!!!!!!!
Furnicuţa şi-a construit un depozit pentru grăunţe .pdf
oof
O zi frumoasa in cutiuţa cu năsip
Tudor Gălăţan a.k.a. How to be or not to be something.
<tex
| Ionescu | 12 | Constanta | Popescu | 24 | Bucuresti | Popescu | 24 | Bucuresti |
log me
LaTeX pe mai multe rânduri:
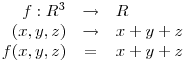
sau:
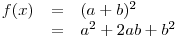
Tabel mic:d
| A | B | A->B |
| 0 | 2 | 3 |
Tabel mare:
| A | B | A->B |
| 1 | 2 | 3 |
Tabel si mai mare:
| A | B | A->B |
| 1 | 2 | 3 |
Diacritice:
Straşnic de îngâmfat, ţăranul crapă streaşina.
Straşnic de îngâmfat, ţăranul crapă streaşina.
In Windows XP sp2 cu IE6 fara update de font se vede asa:

Ordered list:
- 1st item
- 2nd item
Use only F/OSS, Microsft sucks ;) just because I say so.
Love Linux, beacuse I say so.
However, on a GNU system NEVER type <b>sudo make me sandwich</b> , and expect the results...
¡Entendido, amigo!
x
y
a weirdo put this text here
yey im playing with bleach
hi my name is cosine dabe ur frind dont tuch my gotye
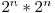
Vivi's blog
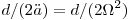
* 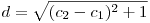
p. 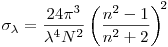
Avem suport pentru 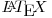 !
!
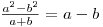
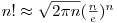
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
| test | test |
Worship me
Feel free to plghay around, but Big Brother is watching you.
What does this button do?
lalallaa
Intrebare: cum poti seta culoarea cu care scrii?
Uite asa: scris cu rosu
Siteul sub IE 7 -- vezi pagina dedicata
Siteul sub FF 2 - mica problema panoul de 'editeaza', 'vezi istoria', 'sterge' etc (in IE7 panoul nu se suprapune)

[test]
OMG test, good work people :D
Acuma doar trebuie putin stimulata comunitatea
[/test]
Interesting choice of words.
a very bold MAN
CAPSOMANII-I DESPISE THEM
gasise pe-un teren viran,
un geamantan.
si-n geamantan,
un pachet.
si in pachet,
un pachetel gasise el.
si-n pachetel,
alt pachetel.
si-un pachetel in pachetel,
legat cu funde elegante.
si-n pachetel...vreo 40 de diamante...
...
Adio voi...va las si plec fiindca mi-e dor...
si a plecat Apolodor
!!!<>
tralalala blablabla lala
salut, aici poate sa scrie oricine ce vrea? Robert
| 1 | 2 | 3 |
|---|---|---|
| unu | doi | trei |
| 1... unu | 2... doi | 3... trei |
Moraru Ionut has been here. :))
shnako was here :)
:) gosh...
inca unul, de tipul cel mai heyyyyyyyyyy prost din corcodus, se joaca cu in nisip.. ura ...
cel mai prost din corcodus a terminat... altcineva?:D
tot el: atentie fratilor ne urmareste big brother 3 (sau 4)
Care imi da o lopata ? :)
// comentariu
#include <cstdio> // comment1
// comment2
int main()
{
return 0;
}| Latura 1 | Latura 2 | Latura 3 | Latura 4 | Latura 2 | Latura 3 | Latura 1 |
|---|---|---|---|---|---|---|
| 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 |
&6 7 8&
# Hello
## Hello 2
### Hello 3

Subsir 2
(problema grea clasa a 9a, problema medie clasa a 10a, problema usoara clasele 11-12)
Problema poate fi considerata asemanatoare cu cea a celui mai lung subsir crescator, avand o rezolvare similara de complexitatea O(N2) folosind metoda programarii dinamice.
Se vor construi doi vectori:
- Ai = lungimea celui mai scurt subsir crescator maximal care incepe cu pozitia i
- Ti = urmatorul element dupa pozitia i in cel mai scurt subsir crescator maximal care incepe cu i (pentru reconstiutire)
Pentru fiecare i, se va cauta un j > i astfel incat Vi ≤ Vj (unde V este vectorul de numere) si se alege acela cu Aj minim, Ai devenind Aj+1, iar Ti devine j. Daca nu exista nici un j, Ai se initializeaza cu 1 si Ti cu i.
Ca sirul construit sa fie maximal trebuie ca atunci cand verificam j-urile pentru un i fixat, j-ul respectiv sa fie "dominant", in sensul ca sa nu existe un i < k < j astfel incat Vi ≤ Vk ≤ Vj, deoarece sirul construit cu primul element in i si al doilea in j ar putea fi extins inserand k intre i si j. Verificarea pentru acest k se poate face in O(N), obtinand o solutie O(N3) care ar fi adus 50-60p. Pentru a face verificarea in O(1), facem observatia ca ne intereseaza doar acel Vk minim care este ≥ Vi. Pe masura ce se avanseaza cu variabila j, se pastreaza o variabila min, reprezentand minimul dintre valorile Vj parcurse pana acum, care sunt ≥ Vi.
Astfel, cand se ajunge la un j, se verifica inainte daca Vj < min (conditie necesara pentru a construi un sir maximal). Un ultim detaliu in solutie este obtinerea solutiei minime din punct de vedere lexicografic. Cand se selecteaza j-ul pentru fiecare i, pe langa faptul ca se alege acela cu Aj minim, in caz de egalitate se va alege acela cu valoarea Vj minima. Selectarea este corecta deoarece nu vor exista j1, j2 cu Aj1 si Aj2 minim , iar Vj1 = Vj2.
Problema se poate rezolva mai bine intr-o complexitate O(N*lg2 N) folosind structuri de date avansate, astfel transformandu-se intr-o problema de clasele 11-12 grea, sau chiar o problema de finala. Lasam aceasta rezolvare ca exercitiu pentru cititor.
Sum
(problema usoara, clasa a 10a)
Vom face o prima observatie:
- (n, d) = 1 <=> (n, n - d) = 1, (n, n + d) = 1
Fie a = phi (n), indicatorul lui Euler. Fie b numarul de numere prime cu n cuprinse intre n si 2 * n.
Deoarece (n, d) = 1 <=> (n, n + d) = 1, a ≤ b. Deoarece (n, d) = 1 <=> (n, n - d) = 1, b ≤ a => b = a. Fie x1, x2, .. xa numerele < n si prime cu n => numerele cuprinse intre n si 2 * n si prime cu n vor fi x1 + n, x2 + n, .. xa + n.
Conform observatiei facute, (n, n - x1) = 1, (n, n - x2) = 1, .. (n, n - xa) = 1 =>
xa = n - x1 <=> x1 + xa = n
xa-1 = n - x2 <=> x2 + xa-1 = n
...
x1 = n - xa <=> xa + x1 = n
Fie S1 suma numerelor prime cu n si mai mici ca n, fie S2 suma numerelor prime cu n, cuprinse intre n si 2 * n.
Adunand cele a egalitati, obtinem 2 * S1 = a * n => S1 = (a * n) / 2.
S2 = a * n + S1 => S1 + S2 = 2 * a * n.
Se foloseste o singura data ciurul lui Erathostene pentru a determina functia phi pentru toate intrebarile. Se poate consulta articolul despre cirulul lui Erathostene.
Pavare 2
(problema grea, clasa a 10a)
Problema se rezolva cu programare dinamica. Utilizam urmatoare structura de date:
- V[i][j][0] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie albe
- V[i][j][1] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie negre
Relatiile de recurenta sunt acum usor de dedus. Odata calculata matricea putem raspunde foarte usor primei cerinte, facand suma V[N][i][0] (pentru 1 ≤ i ≤ A) si V[N][i][1] pentru (1 ≤ i ≤ B).
Pentru a 2-a cerinta incercam sa construim a K-a secventa lexicografica de la inceput catre sfarsit. Astfel, la fiecare pas incercam sa punem o segventa de tipul '0...01' care sa contina un numar maxim de '0'. Daca la pasul curent nu putem pune nici un '0' atunci vom pune o secventa de tipul '1..1' care sa contina un numar minim de 1. Numarul de '0'-uri sau de '1' pe care il punem il vom calcula cu ajutorul matricei precalculate la prima cerinta. Astfel, daca putem pune p de '0' inseamna ca numarul de posibilitati pentru a completa restul solutiei daca punem cel putin p de '0' la inceput este mai mare sau egal cu K. Alegem cel mai mare numar p cu proprietatea de mai sus. Daca p nu exista, incercam sa punem cat mai putini '1' in aceeasi maniera. Continuam apoi cu restul secventei, iar din K scadem numarul de solutii peste care am "sarit".
Tare de tot acest sandbox :)
* Re: chiar ca e! poti sa te joci cu css aici :)
![\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &
\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &](http://www.infoarena.ro/static/images/latex/eef80f4248abc3249af6c045a561bf56_13.50015pt.gif)
scrieti "assert(fail)" la inceputul programului la olimpiada si merge de aprox. 10 ori mai rapid programu ca foloseste mai multe core-uri(merge in c++, dar si in c)
h1. KAKTUS
MULTE SMENURI DE PROGRAMARE IN C/C++... SI NU NUMAI!!!!!!!
Furnicuţa şi-a construit un depozit pentru grăunţe .pdf
oof
O zi frumoasa in cutiuţa cu năsip
Tudor Gălăţan a.k.a. How to be or not to be something.
<tex
| Ionescu | 12 | Constanta | Popescu | 24 | Bucuresti | Popescu | 24 | Bucuresti |
log me
LaTeX pe mai multe rânduri:
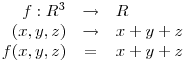
sau:
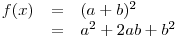
Tabel mic:d
| A | B | A->B |
| 0 | 2 | 3 |
Tabel mare:
| A | B | A->B |
| 1 | 2 | 3 |
Tabel si mai mare:
| A | B | A->B |
| 1 | 2 | 3 |
Diacritice:
Straşnic de îngâmfat, ţăranul crapă streaşina.
Straşnic de îngâmfat, ţăranul crapă streaşina.
In Windows XP sp2 cu IE6 fara update de font se vede asa:

Ordered list:
- 1st item
- 2nd item
Use only F/OSS, Microsft sucks ;) just because I say so.
Love Linux, beacuse I say so.
However, on a GNU system NEVER type <b>sudo make me sandwich</b> , and expect the results...
¡Entendido, amigo!
x
y
a weirdo put this text here
yey im playing with bleach
hi my name is cosine dabe ur frind dont tuch my gotye
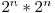
Vivi's blog
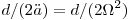
* 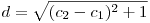
p. 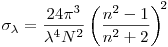
Avem suport pentru 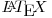 !
!
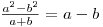
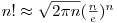
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
| test | test |
Worship me
Feel free to plghay around, but Big Brother is watching you.
What does this button do?
lalallaa
Intrebare: cum poti seta culoarea cu care scrii?
Uite asa: scris cu rosu
Siteul sub IE 7 -- vezi pagina dedicata
Siteul sub FF 2 - mica problema panoul de 'editeaza', 'vezi istoria', 'sterge' etc (in IE7 panoul nu se suprapune)

[test]
OMG test, good work people :D
Acuma doar trebuie putin stimulata comunitatea
[/test]
Interesting choice of words.
a very bold MAN
CAPSOMANII-I DESPISE THEM
gasise pe-un teren viran,
un geamantan.
si-n geamantan,
un pachet.
si in pachet,
un pachetel gasise el.
si-n pachetel,
alt pachetel.
si-un pachetel in pachetel,
legat cu funde elegante.
si-n pachetel...vreo 40 de diamante...
...
Adio voi...va las si plec fiindca mi-e dor...
si a plecat Apolodor
!!!<>
tralalala blablabla lala
salut, aici poate sa scrie oricine ce vrea? Robert
| 1 | 2 | 3 |
|---|---|---|
| unu | doi | trei |
| 1... unu | 2... doi | 3... trei |
Moraru Ionut has been here. :))
shnako was here :)
:) gosh...
inca unul, de tipul cel mai heyyyyyyyyyy prost din corcodus, se joaca cu in nisip.. ura ...
cel mai prost din corcodus a terminat... altcineva?:D
tot el: atentie fratilor ne urmareste big brother 3 (sau 4)
Care imi da o lopata ? :)
// comentariu
#include <cstdio> // comment1
// comment2
int main()
{
return 0;
}| Latura 1 | Latura 2 | Latura 3 | Latura 4 | Latura 2 | Latura 3 | Latura 1 |
|---|---|---|---|---|---|---|
| 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 |
&6 7 8&
# Hello
## Hello 2
### Hello 3

Subsir 2
(problema grea clasa a 9a, problema medie clasa a 10a, problema usoara clasele 11-12)
Problema poate fi considerata asemanatoare cu cea a celui mai lung subsir crescator, avand o rezolvare similara de complexitatea O(N2) folosind metoda programarii dinamice.
Se vor construi doi vectori:
- Ai = lungimea celui mai scurt subsir crescator maximal care incepe cu pozitia i
- Ti = urmatorul element dupa pozitia i in cel mai scurt subsir crescator maximal care incepe cu i (pentru reconstiutire)
Pentru fiecare i, se va cauta un j > i astfel incat Vi ≤ Vj (unde V este vectorul de numere) si se alege acela cu Aj minim, Ai devenind Aj+1, iar Ti devine j. Daca nu exista nici un j, Ai se initializeaza cu 1 si Ti cu i.
Ca sirul construit sa fie maximal trebuie ca atunci cand verificam j-urile pentru un i fixat, j-ul respectiv sa fie "dominant", in sensul ca sa nu existe un i < k < j astfel incat Vi ≤ Vk ≤ Vj, deoarece sirul construit cu primul element in i si al doilea in j ar putea fi extins inserand k intre i si j. Verificarea pentru acest k se poate face in O(N), obtinand o solutie O(N3) care ar fi adus 50-60p. Pentru a face verificarea in O(1), facem observatia ca ne intereseaza doar acel Vk minim care este ≥ Vi. Pe masura ce se avanseaza cu variabila j, se pastreaza o variabila min, reprezentand minimul dintre valorile Vj parcurse pana acum, care sunt ≥ Vi.
Astfel, cand se ajunge la un j, se verifica inainte daca Vj < min (conditie necesara pentru a construi un sir maximal). Un ultim detaliu in solutie este obtinerea solutiei minime din punct de vedere lexicografic. Cand se selecteaza j-ul pentru fiecare i, pe langa faptul ca se alege acela cu Aj minim, in caz de egalitate se va alege acela cu valoarea Vj minima. Selectarea este corecta deoarece nu vor exista j1, j2 cu Aj1 si Aj2 minim , iar Vj1 = Vj2.
Problema se poate rezolva mai bine intr-o complexitate O(N*lg2 N) folosind structuri de date avansate, astfel transformandu-se intr-o problema de clasele 11-12 grea, sau chiar o problema de finala. Lasam aceasta rezolvare ca exercitiu pentru cititor.
Sum
(problema usoara, clasa a 10a)
Vom face o prima observatie:
- (n, d) = 1 <=> (n, n - d) = 1, (n, n + d) = 1
Fie a = phi (n), indicatorul lui Euler. Fie b numarul de numere prime cu n cuprinse intre n si 2 * n.
Deoarece (n, d) = 1 <=> (n, n + d) = 1, a ≤ b. Deoarece (n, d) = 1 <=> (n, n - d) = 1, b ≤ a => b = a. Fie x1, x2, .. xa numerele < n si prime cu n => numerele cuprinse intre n si 2 * n si prime cu n vor fi x1 + n, x2 + n, .. xa + n.
Conform observatiei facute, (n, n - x1) = 1, (n, n - x2) = 1, .. (n, n - xa) = 1 =>
xa = n - x1 <=> x1 + xa = n
xa-1 = n - x2 <=> x2 + xa-1 = n
...
x1 = n - xa <=> xa + x1 = n
Fie S1 suma numerelor prime cu n si mai mici ca n, fie S2 suma numerelor prime cu n, cuprinse intre n si 2 * n.
Adunand cele a egalitati, obtinem 2 * S1 = a * n => S1 = (a * n) / 2.
S2 = a * n + S1 => S1 + S2 = 2 * a * n.
Se foloseste o singura data ciurul lui Erathostene pentru a determina functia phi pentru toate intrebarile. Se poate consulta articolul despre cirulul lui Erathostene.
Pavare 2
(problema grea, clasa a 10a)
Problema se rezolva cu programare dinamica. Utilizam urmatoare structura de date:
- V[i][j][0] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie albe
- V[i][j][1] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie negre
Relatiile de recurenta sunt acum usor de dedus. Odata calculata matricea putem raspunde foarte usor primei cerinte, facand suma V[N][i][0] (pentru 1 ≤ i ≤ A) si V[N][i][1] pentru (1 ≤ i ≤ B).
Pentru a 2-a cerinta incercam sa construim a K-a secventa lexicografica de la inceput catre sfarsit. Astfel, la fiecare pas incercam sa punem o segventa de tipul '0...01' care sa contina un numar maxim de '0'. Daca la pasul curent nu putem pune nici un '0' atunci vom pune o secventa de tipul '1..1' care sa contina un numar minim de 1. Numarul de '0'-uri sau de '1' pe care il punem il vom calcula cu ajutorul matricei precalculate la prima cerinta. Astfel, daca putem pune p de '0' inseamna ca numarul de posibilitati pentru a completa restul solutiei daca punem cel putin p de '0' la inceput este mai mare sau egal cu K. Alegem cel mai mare numar p cu proprietatea de mai sus. Daca p nu exista, incercam sa punem cat mai putini '1' in aceeasi maniera. Continuam apoi cu restul secventei, iar din K scadem numarul de solutii peste care am "sarit".
Tare de tot acest sandbox :)
* Re: chiar ca e! poti sa te joci cu css aici :)
![\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &
\[
viz[i][ j]=
\begin{cases}
1,& \text{daca } n \cdot 2^{i} \cdot 3^{j} $\text{ a fost deja generat}$ \\
0, & \text{altfel}
\end{cases}
\] &](http://www.infoarena.ro/static/images/latex/eef80f4248abc3249af6c045a561bf56_13.50015pt.gif)
scrieti "assert(fail)" la inceputul programului la olimpiada si merge de aprox. 10 ori mai rapid programu ca foloseste mai multe core-uri(merge in c++, dar si in c)
h1. KAKTUS
MULTE SMENURI DE PROGRAMARE IN C/C++... SI NU NUMAI!!!!!!!
Furnicuţa şi-a construit un depozit pentru grăunţe .pdf
oof
O zi frumoasa in cutiuţa cu năsip
Tudor Gălăţan a.k.a. How to be or not to be something.
<tex
| Ionescu | 12 | Constanta | Popescu | 24 | Bucuresti | Popescu | 24 | Bucuresti |
log me
LaTeX pe mai multe rânduri:
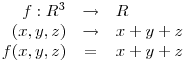
sau:
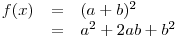
Tabel mic:d
| A | B | A->B |
| 0 | 2 | 3 |
Tabel mare:
| A | B | A->B |
| 1 | 2 | 3 |
Tabel si mai mare:
| A | B | A->B |
| 1 | 2 | 3 |
Diacritice:
Straşnic de îngâmfat, ţăranul crapă streaşina.
Straşnic de îngâmfat, ţăranul crapă streaşina.
In Windows XP sp2 cu IE6 fara update de font se vede asa:

Ordered list:
- 1st item
- 2nd item
Use only F/OSS, Microsft sucks ;) just because I say so.
Love Linux, beacuse I say so.
However, on a GNU system NEVER type <b>sudo make me sandwich</b> , and expect the results...
¡Entendido, amigo!
x
y
a weirdo put this text here
yey im playing with bleach
hi my name is cosine dabe ur frind dont tuch my gotye
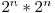
Vivi's blog
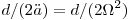
* 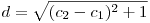
p. 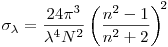
Avem suport pentru 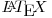 !
!
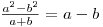
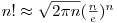
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
| test | test |
Worship me
Feel free to plghay around, but Big Brother is watching you.
What does this button do?
lalallaa
Intrebare: cum poti seta culoarea cu care scrii?
Uite asa: scris cu rosu
Siteul sub IE 7 -- vezi pagina dedicata
Siteul sub FF 2 - mica problema panoul de 'editeaza', 'vezi istoria', 'sterge' etc (in IE7 panoul nu se suprapune)

[test]
OMG test, good work people :D
Acuma doar trebuie putin stimulata comunitatea
[/test]
Interesting choice of words.
a very bold MAN
CAPSOMANII-I DESPISE THEM
gasise pe-un teren viran,
un geamantan.
si-n geamantan,
un pachet.
si in pachet,
un pachetel gasise el.
si-n pachetel,
alt pachetel.
si-un pachetel in pachetel,
legat cu funde elegante.
si-n pachetel...vreo 40 de diamante...
...
Adio voi...va las si plec fiindca mi-e dor...
si a plecat Apolodor
!!!<>
tralalala blablabla lala
salut, aici poate sa scrie oricine ce vrea? Robert
| 1 | 2 | 3 |
|---|---|---|
| unu | doi | trei |
| 1... unu | 2... doi | 3... trei |
Moraru Ionut has been here. :))
shnako was here :)
:) gosh...
inca unul, de tipul cel mai heyyyyyyyyyy prost din corcodus, se joaca cu in nisip.. ura ...
cel mai prost din corcodus a terminat... altcineva?:D
tot el: atentie fratilor ne urmareste big brother 3 (sau 4)
Care imi da o lopata ? :)
// comentariu
#include <cstdio> // comment1
// comment2
int main()
{
return 0;
}| Latura 1 | Latura 2 | Latura 3 | Latura 4 | Latura 2 | Latura 3 | Latura 1 |
|---|---|---|---|---|---|---|
| 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0 |
&6 7 8&
# Hello
## Hello 2
### Hello 3

Subsir 2
(problema grea clasa a 9a, problema medie clasa a 10a, problema usoara clasele 11-12)
Problema poate fi considerata asemanatoare cu cea a celui mai lung subsir crescator, avand o rezolvare similara de complexitatea O(N2) folosind metoda programarii dinamice.
Se vor construi doi vectori:
- Ai = lungimea celui mai scurt subsir crescator maximal care incepe cu pozitia i
- Ti = urmatorul element dupa pozitia i in cel mai scurt subsir crescator maximal care incepe cu i (pentru reconstiutire)
Pentru fiecare i, se va cauta un j > i astfel incat Vi ≤ Vj (unde V este vectorul de numere) si se alege acela cu Aj minim, Ai devenind Aj+1, iar Ti devine j. Daca nu exista nici un j, Ai se initializeaza cu 1 si Ti cu i.
Ca sirul construit sa fie maximal trebuie ca atunci cand verificam j-urile pentru un i fixat, j-ul respectiv sa fie "dominant", in sensul ca sa nu existe un i < k < j astfel incat Vi ≤ Vk ≤ Vj, deoarece sirul construit cu primul element in i si al doilea in j ar putea fi extins inserand k intre i si j. Verificarea pentru acest k se poate face in O(N), obtinand o solutie O(N3) care ar fi adus 50-60p. Pentru a face verificarea in O(1), facem observatia ca ne intereseaza doar acel Vk minim care este ≥ Vi. Pe masura ce se avanseaza cu variabila j, se pastreaza o variabila min, reprezentand minimul dintre valorile Vj parcurse pana acum, care sunt ≥ Vi.
Astfel, cand se ajunge la un j, se verifica inainte daca Vj < min (conditie necesara pentru a construi un sir maximal). Un ultim detaliu in solutie este obtinerea solutiei minime din punct de vedere lexicografic. Cand se selecteaza j-ul pentru fiecare i, pe langa faptul ca se alege acela cu Aj minim, in caz de egalitate se va alege acela cu valoarea Vj minima. Selectarea este corecta deoarece nu vor exista j1, j2 cu Aj1 si Aj2 minim , iar Vj1 = Vj2.
Problema se poate rezolva mai bine intr-o complexitate O(N*lg2 N) folosind structuri de date avansate, astfel transformandu-se intr-o problema de clasele 11-12 grea, sau chiar o problema de finala. Lasam aceasta rezolvare ca exercitiu pentru cititor.
Sum
(problema usoara, clasa a 10a)
Vom face o prima observatie:
- (n, d) = 1 <=> (n, n - d) = 1, (n, n + d) = 1
Fie a = phi (n), indicatorul lui Euler. Fie b numarul de numere prime cu n cuprinse intre n si 2 * n.
Deoarece (n, d) = 1 <=> (n, n + d) = 1, a ≤ b. Deoarece (n, d) = 1 <=> (n, n - d) = 1, b ≤ a => b = a. Fie x1, x2, .. xa numerele < n si prime cu n => numerele cuprinse intre n si 2 * n si prime cu n vor fi x1 + n, x2 + n, .. xa + n.
Conform observatiei facute, (n, n - x1) = 1, (n, n - x2) = 1, .. (n, n - xa) = 1 =>
xa = n - x1 <=> x1 + xa = n
xa-1 = n - x2 <=> x2 + xa-1 = n
...
x1 = n - xa <=> xa + x1 = n
Fie S1 suma numerelor prime cu n si mai mici ca n, fie S2 suma numerelor prime cu n, cuprinse intre n si 2 * n.
Adunand cele a egalitati, obtinem 2 * S1 = a * n => S1 = (a * n) / 2.
S2 = a * n + S1 => S1 + S2 = 2 * a * n.
Se foloseste o singura data ciurul lui Erathostene pentru a determina functia phi pentru toate intrebarile. Se poate consulta articolul despre cirulul lui Erathostene.
Pavare 2
(problema grea, clasa a 10a)
Problema se rezolva cu programare dinamica. Utilizam urmatoare structura de date:
- V[i][j][0] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie albe
- V[i][j][1] = numarul de posibilitati pentru a pava i metri astfel incat primele j placi sa fie negre
Relatiile de recurenta sunt acum usor de dedus. Odata calculata matricea putem raspunde foarte usor primei cerinte, facand suma V[N][i][0] (pentru 1 ≤ i ≤ A) si V[N][i][1] pentru (1 ≤ i ≤ B).
Pentru a 2-a cerinta incercam sa construim a K-a secventa lexicografica de la inceput catre sfarsit. Astfel, la fiecare pas incercam sa punem o segventa de tipul '0...01' care sa contina un numar maxim de '0'. Daca la pasul curent nu putem pune nici un '0' atunci vom pune o secventa de tipul '1..1' care sa contina un numar minim de 1. Numarul de '0'-uri sau de '1' pe care il punem il vom calcula cu ajutorul matricei precalculate la prima cerinta. Astfel, daca putem pune p de '0' inseamna ca numarul de posibilitati pentru a completa restul solutiei daca punem cel putin p de '0' la inceput este mai mare sau egal cu K. Alegem cel mai mare numar p cu proprietatea de mai sus. Daca p nu exista, incercam sa punem cat mai putini '1' in aceeasi maniera. Continuam apoi cu restul secventei, iar din K scadem numarul de solutii peste care am "sarit".
Tare de tot acest sandbox :)
* Re: chiar ca e! poti sa te joci cu css aici :)











































































































































































































 hmmmmm interesting marmot
hmmmmm interesting marmotTOIE was here
www.infoarena.ro/toie
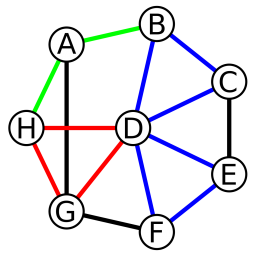 Am rezolvat asta pentru tine, nu merg HTML tags
Am rezolvat asta pentru tine, nu merg HTML tags
Am gasit pe dark web solutiile la problemele de la IOI 2021 !!1! click aici
skibidi toilet a dat rizz up la 1 sau 2 gyatturi masive
