În materie de rezultate la competiţiile internaţionale (liceu şi facultate), anul 2017 se poate mândri ca fiind unul dintre cei mai buni, comparându-se cu vestitul 2012.

Cu o mică întârziere, vă invit să rememorăm cele mai frumoase şi interesante momente la care echipa Infoarena, împreună cu comunitatea Infoarena, a asistat pe parcursul acestui an îmbelşugat.

Aşa că luaţi-vă un pahar cu ce vreţi voi, admiraţi şi salivaţi la tortul Infoarena şi să începem:

Rezultat fabulos obţinut la IOI

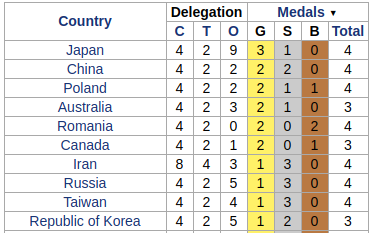
Anul 2017 a adus României două noi medalii de aur. Constantin-Buliga Stefan •fanache99 şi Tamio Vesa Nakajima •tamionv au reuşit să se lupte până la capăt, obţinând astfel locurile 11, respectiv 15. Alături de aceştia, Oncescu Costin •geniucos şi Andrei Constantinescu •Andrei1998 (foşti medaliaţi cu argint) au obţinut 2 medalii de bronz, situând astfel România pe locul 5 în clasamentul pe ţări (cel mai bun rezultat din 2012 încoace). Dar să lăsăm screenshot-urile să vorbească: (sursa: stats.ioinformatics.org).

I-am rugat pe cei doi medaliaţi cu aur să ne scrie câteva păreri despre participarea la olimpiadă, pe care vi le las aici:

Constantin-Buliga Stefan •fanache99 :

Din punct de vedere al informaticii, mi-a placut trains din prima zi, are un jmen destul de dragut si util care initial nu pare neaparat ca merge (si mna, am scos-o in concurs, normal ca imi place :)) ), dar si problema cu queryuri de arbori partiali din a doua zi, nu mai stiu numele, pentru ca, in sine, era o problema grea atat de tehnica, cat si de idee. Experienta de Iran a fost una interesanta cel putin. M-a lovit un pic diferenta de culturi si cum ei chiar sunt obisnuiti cu a lor si nu li se pare nimic dubios in a avea tablouri cu liderul lor peste tot, ca un fel de icoane.

Tamio Vesa Nakajima •tamionv :

Mi s-a parut ca organizarea concursului a fost foarte buna, in special cand vine vorba de probleme, care au si interesante in sine, dar si cu un text clar si nostim. Problemele mele favorite au fost wiring si nowruz. Wiring e o problema excelenta de informatica “clasica”: 2-3 observatii, un brut si o optimizare de la O(n^2) la O(nlog(n)). Nowruz mi-a placut pentru ca a fost o problema de constructie ce-ti cere ceva interesant si original. Social, mi s-a parut foarte distractiv sa ma intalnesc cu olimpici internationali din mai multe tari, dintre care acuma unii imi sunt si colegi de facultate.

Îi felicităm pe toţi şi le urăm succes în anul care urmează.

Rezultate excepţionale la ACM-ICPC

Dacă aţi citit retrospectiva anului trecut, puteţi observa o secţiune în care este specificat faptul că, la nivel universitar, România participă pentru prima dată de foarte mulţi ani cu două echipe la finala ACM-ICPC. Cele două echipe date de Universitatea Politehnică Bucureşti (TeamName) şi Universitatea din Bucureşti (Echipa Lachetă) au obţinut rezultate bune, ocupând locurile 47, respectiv 28.

În anul care urmează, România va fi reprezentată la finala ACM ICPC 2018 de către noua Echipa Lachetă (versiunea 2.5) a Universităţii Bucureşti, formată din (de la stânga la dreapta în poză:

• Popa Andrei •andreiiii
• Alex Velea •veleandu
• Lucian Bicsi •retrograd
• Mihai Calancea •klamathix (Coach).

Ei au reuşit o performanţă de excepţie la SEERC 2017, nu numai obţinând locul I (pentru prima dată ocupat de români în ultimii 13 ani), dar şi devansând echipa clasată pe locul al doilea cu 2 probleme.

De asemenea, deşi nu vor concura sub steagul României, Universitatea Oxford din UK se poate mândri cu cei 3 români (toţi studenţi în anul 1) care au calificat universitatea la aceeaşi finală mondială. Urăm întregii echipe mult noroc şi ne dorim să obţină un rezultat cât mai frumos la acest concurs. Echipa este formată din:

• Chichirim George •george_stelian
• Andrei Constantinescu •Andrei1998
• Tamio Vesa Nakajima •tamionv
• Jianu Mihail •mihail.jianu (Coach)

Le urăm mult succes la finala ACM care va avea loc între 15 şi 20 aprilie la Beijing.

Aur absolut la BOI şi CEOI

BOI (Balkan Olympiad in Informatics) şi CEOI (Central European Olympiad in Informatics) sunt cele două competiţii internaţionale regionale la care România anual se bate nu numai să iasă în top, ci chiar să câştige locul 1. Întrucât competiţiile ne scutesc de powerhouse-uri precum Rusia şi China, concurenţa la acest nivel rămâne aprigă în momentul în care încerci să detronezi ţări precum Polonia, Bulgaria sau Croaţia. La competiţiile regionale, românilor le place să se mândrească cu medaliile de aur şi argint pe care le obţin, bucuria fiind astfel mult mai mare atunci când obţinem nu doar aur, ci chiar aur ABSOLUT (locul 1).

La Olimpiada Balcanică de Informatică, România a obţinut 2 medalii de aur absolut ( Chichirim George •george_stelian si Tatomir Alex •atatomir), acompaniate de alte 2 medalii de argint.

La Olimpiada Central Europeană de Informatică, România a punctat fabulos, obţinand 3 medalii de aur şi una de argint. Mai mult, una din cele 3 medalii de aur este aur absolut, obţinut de Popa Andrei •andreiiii. CEOI-ul este un concurs recunoscut pentru faptul că nu este foarte uşor să obţii medalie de aur. Acest rezultat excepţional marchează probabil cel mai bun rezultat din istorie al României la olimpiada ţărilor central europene.

Şi dacă tot am deschis subiectul medaliilor de aur absolut, nu putem să nu îl menţionăm şi pe Bogdan Sitaru •bogdan10bos care a obţinut aur absolut la olimpiada Pluridisciplinară din Yakutia.

Nu în ultimul rând, dorim să facem un rezumat prin care felicităm toţi participanţii noştri oficiali la competiţiile internaţionale:

Juniori

• Tinca Matei •TincaMatei - Aur la EJOI, Aur la JBOI, Aur la Shumen
• Tiberiu Musat •Tiberiu02 - Aur la JBOI, Argint la EJOI, Argint la Shumen
• Mirica Matei •MiricaMatei - Argint la EJOI, Argint la JBOI, Argint la Shumen
• Rapeanu George •georgerapeanu - Argint la EJOI, Argint la JBOI
• Boni Daniel Stefan •refugiat - Bronz la Shumen
• Tudor Mocioi •tgm000 - Bronz la Shumen
• Al An Gr •Albert - Bronz la Shumen

Seniori

• Tamio Vesa Nakajima •tamionv - Aur la IOI, Aur la CEOI
• Constantin-Buliga Stefan •fanache99 - Aur la IOI, Aur la Shumen, Argint la BOI
• Oncescu Costin •geniucos - Bronz la IOI, Aur la CEOI, Aur la Shumen
• Andrei Constantinescu •Andrei1998 - Bronz la IOI, Argint la CEOI
• Popa Andrei •andreiiii - Aur absolut la CEOI, Aur la Shumen
• Tatomir Alex •atatomir - Aur absolut la BOI, Aur la Shumen
• Bogdan Sitaru •bogdan10bos - Aur absolut la Yakutia, Argint la Shumen
• Chichirim George •george_stelian - Aur absolut la BOI
• Theodor Moroianu •theodor.moroianu - Argint la BOI, Argint la Yakutia, Argint la Shumen
• Alexandru Petrescu •alexpetrescu - Argint la Yakutia, Bronz la Shumen

2018 şi New Year's Resolutions

La ce ne putem aştepta de la anul care tocmai a început? Cel mai important eveniment planificat pentru 2018 este, desigur, organizarea BOI în România, care are drept consecinţă 4 locuri suplimentare pentru echipa noastră la această competiţie. Astfel, cei calificaţi în lot vor avea mai multe şanse de a prinde o olimpiadă internaţională. De asemenea, cum 2 dintre participanţii la IOI de anul trecut au absolvit liceul, ne putem aştepta la o întrecere strânsă pentru calificarea la cel mai prestigios concurs de liceu, organizat anul acesta în Tokyo, Japonia.

New Year's Resolutions de anul acesta le includ în mod tradiţional şi pe cele de anul trecut (care, recursiv, le includ pe cele pentru 2016 ;) ), cu o adiţie legată mai mult de spiritul competiţiei, decât de partea tehnică sau de pregătire: olimpiadele şi concursurile, deşi le consideraţi importante, nu vă definesc ca oameni. Rezultatele pe care le obţineţi la un concurs nu arată decât cât de bine v-aţi descurcat în acel interval de timp să rezolvaţi cele câteva probleme propuse. Aşa că deznădejdea după obţinerea un rezultat mai slab decât cel aşteptat, încrâncenarea pentru o calificare, sau îngrijorarea că ratarea unei competiţii va fi un minus pe CV sau la admiterea la facultate nu fac decât să vă îndepărteze de ceea ce v-a adus şi v-a ţinut în comunitatea programării competitive: pasiunea de a rezolva probleme de informatică. Aşa că New Year's Resolution pentru 2018 este să nu uitaţi ce vă atrage spre acest domeniu, şi să nu puneţi un preţ mai mare decât cel real pe rezultate.

Facultatea de Ştiinţe Exacte şi Inginereşti din cadrul Universităţii „1 Decembrie 1918” din Alba Iulia lansează un concurs naţional pentru elevii din clasele a XI-a şi a XII-a pasionaţi de informatică.

Concursul se va desfăşura în primăvara anului viitor – 14 Aprilie 2018, înscrierea fiind deschisă din 17 noiembrie 2017. Termenul final de înscriere este 7 Aprilie 2018.

În cadrul concursului se vor oferi premii în bani totalizând 15000 lei.

De asemenea, concurenţilor premianţi li se oferă anumite facilităţi la Concursul de Admitere 2018, în cazul în care vor opta pentru specializarea Informatică din cadrul Facultăţii de Ştiinţe Exacte şi Inginereşti a Universităţii „1 Decembrie 1918” din Alba Iulia, mai multe detalii fiind menţionate în regulamentul concursului.

Concursul este organizat în parteneriat cu Consiliul Judeţean Alba, Inspectoratul Şcolar Judeţean Alba şi Casa Corpului Didactic Alba. Sponsorul evenimentului este firma Optimal Programs SRL.

Concursul se adresează elevilor de clasele a XI-a şi a XII-a din România, indiferent de profilul liceului sau specializarea urmată.

În plus, gazdele vin în întâmpinarea elevilor, oferindu-le în lunile următoare cursuri de pregătire în domeniul Informaticii. Cursanţii nu sunt condiţionaţi de participarea la concursul naţional in4it-UAB. Astfel, echipa de organizare propune un format inedit prin care toţi liceenii pasionaţi de informatică sunt sprijiniţi şi încurajaţi să participe la concurs, la admiterea la facultate sau să opteze pentru o carieră în domeniul IT.

Pentru informaţii suplimentare vizitaţi pagina web a concursului: www.uab.ro/in4it.

Vă anunţăm cu mare plăcere că finala Algoritmiada 2017 va avea loc în perioada 2-5 noiembrie, la Craiova. Mulţumim domnului Marius Nicoli •mariusn01 pentru primire, ajutorul în organizare, cât şi pentru găsirea noilor sponsori Oxygen şi Caphyon. Programul complet al weekend-ului îl puteţi găsi aici.

Puteţi găsi aici lista cu concurenţii calificaţi la runda finală. Criteriile de calificare presupun aflarea clasei fiecărui concurent, iar pentru cei de gimnaziu nu am putut afla întotdeauna această informaţie. Dacă credeţi că, conform regulamentului, sunteţi calificaţi la runda finală, vă rugăm să scrieţi un comentariu la acest post pentru a vă putea trece pe listă. De asemenea, rugăm şi pe ceilalţi concurenţi să verifice lista şi să ne semnaleze eventualele greşeli, deoarece această listă nu e finală şi poate suferi modificări. Dacă unii concurenţi nu pot participa, locurile lor sunt redistribuite.

Cei mai atenţi pot observa că Tamio Vesa Nakajima •tamionv nu apare în lista calificaţilor, deşi ar trebui. Asta se datorează faptului că a devenit membru al echipei infoarena! Îi urăm bun venit în echipă şi spor la treabă! ;)

Calificati Juniori:

Nume	Clasa
Rapeanu George •georgerapeanu	8
Donciu Mircea •Mircea_Donciu	8
Ciuperceanu Vlad •LeVladz	7
Nicola Alexandra Mihaela •Nicolaalexandra	7
Dart Monkey •lucametehau	6
Alex Luchianov •AlexandruLuchianov1	6
?	5
?	5
Tiberiu Musat •Tiberiu02	8
Tinca Matei •TincaMatei	8
Popescu Ioan •gioto	8
Coroian David •Coroian_David	8
Nanu Ruxandra Laura •Ruxandra985	8
Nicolae Radu •RaduXD1	8
Stefan Dascalescu •stefdascalescu	9
Mirica Matei •MiricaMatei	8
Gheorghe Liviu Armand •armighe	8

Calificati Seniori:

Nume	Clasa
Emanuel Nrx •StarGold2	9
Udristoiu Alexandra Maria •alexandra_udristoiu	9
Alexa Tudose •Alexa2001	9
Alexandru Petrescu •alexpetrescu	10
Bogdan Sitaru •bogdan10bos	10
Laura Georgescu •laurageorgescu	10
Oncescu Costin •geniucos	11
Tatomir Alex •atatomir	11
Constantin-Buliga Stefan •fanache99	11
Chichirim George •george_stelian	12
Andrei Constantinescu •Andrei1998	12
Iordache Ioan-Bogdan •iordache.bogdan	12
Lucian Bicsi •retrograd	Open
Radu Muntean •heracle	Open
Mihai Nitu •Impaler_009	Open
Dan-Constantin Spatarel •spatarel	Open
Babalau Alexandru •alex_Harry	11
Cozma Tudor •tudi98	12
Gabi Tulba-Lecu •GabiTulba	11
Chris Luntraru •Brandon	12
Ana Kapros •akapros	10
Ozturk Arif •pepsiM4A1	11
Theodor Moroianu •theodor.moroianu	10
turcuman vlad •vladtt	10
Serban Cercelescu •oldatlantian	10
Dobre Bogdan Mihai •dobrebogdan	12
Andrei Stanciu •assa98	12
Turdean Alexandru •alexmisto342	12
Andi Arnautu •andrei.arnautu	12
Puscasu Felix •felixi	10

Un feature pe care îl asteptaţi de multă vreme, sursele libere la toate problemele din arhivă, a fost lansat astăzi! Mulţumim lui Adrian Budau •freak93 pentru că l-a implementat!

Pentru că ştim cu toţii ce zicea Uncle Ben, am dorit să ne asigurăm că folosiţi corect această posibilitate de a vedea sursele altor concurenţi. De aceea, înainte de a accesa pentru prima oară o sursă a unei probleme pe care nu aveţi deja 100 de puncte, veţi primi următorul text:

Acest mesaj apare deoarece încerci să vizualizezi o sursă a unei probleme la care nu ai punctaj maxim. Feature-ul de surse libere a fost lansat pentru a nu restricţiona accesul utilizatorilor la nicio sursă şi a le oferi toate resursele posibile pentru a progresa. Cu toate acestea, modul în care fiecare învăţă optim diferă de la persoană la persoană, iar a vedea această sursă poate să nu fie neapărat spre beneficiul tău. De aceea te sfătuim să nu continui dacă:

1. Nu te-ai gândit serios la această problemă. 5 minute nu sunt suficiente pentru a găsi soluţia niciunei probleme. Gândeşte-te serios măcar câteva ore. Cere apoi hint-uri pe forum. Revino aici doar ca ultimă variantă.
2. Ai observat că ai învăţat mai mult rezolvând probleme la care nu ai avut acces la surse. Tentaţia poate fi mare, însă dacă nu te uiţi vei progresa mai mult. :)
3. Problema face parte dintr-o temă pe care ar trebui să o rezolvi independent. Nu este onest să copiezi, iar profesorul tău va şti că ai copiat.
4. Nu cunoşti algoritmii sau structurile de date necesare pentru a rezolva această problemă: în acest caz îţi recomandăm să verifici întâi arhiva educaţională.

În schimb, îţi recomandăm să continui dacă:

1. Ai obţinut un scor mare, dar nu maxim, şi doreşti să vezi posibile optimizări sau stiluri diferite de implementare.
2. Eşti profesor pregătitor şi doreşti să vezi sursele elevilor tăi.
3. Cineva ţi-a recomandat această sursă pentru a învăţa un algoritm nou.

Nu dorim ca acest text să fie un impediment în procesul vostru de învăţare; ne dorim să fie o reamintire a motivelor de a vedea o sursă pe care noi le considerăm corecte şi optime pentru a progresa, şi să vă ofere posibilitatea de a vă răzgândi în cazul în care aveţi un moment de "slăbiciune". :)

În acelaşi timp, suntem conştienţi că nu toţi utilizatorii vor respecta aceste principii. Din acest motiv, clasamentele arhivelor de probleme nu mai pot fi accesate din linkul Clasament din stânga paginii (care arată acum doar clasamentul după rating), pentru a evidenţia scăderea lor ca relevanţă. Ele pot fi accesate în continuare de pe paginile arhivelor.

În încheiere, sperăm că acest feature nou să vă ajute să progresaţi. Folosiţi-l cu înţelepciune!

Linear algebra is very useful in engineering. Usually in school it's a dry subject. The problems seem to be solved by mechanically following some rules without much intuition behind them.

Catalin Tiseanu recommended a short course on youtube with very good insights about geometrical intuition behind linear algebra concepts. I've enjoyed watching it and I highly recommend it.
Essence of linear algebra
Thanks Catalin!

For a Machine Learning view of Linear Algebra you can go through chapter 2 of the Deep Learning Book available online
Deep Learning, Chapter 2: Linear Algebra

I recently attended a Q&A session about this chapter and deep learning in general given by Yaroslav Bulatov (OpenAi, previously Google Street View). It has interesting content for all levels. You might even hear my voice asking tons of questions :).
Yaroslav Bulatov (OpenAi) Q&A Deep Learning Book, Chapter 2: Linear Algebra 

The best introductory linear algebra resource is Gilbert Strang's course taught MIT. He explains things very clearly and with a lot of simple examples. It's all available on youtube!
Gilbert Strang MIT Linear Algebra Video Lectures
You may want to play it at 1.5 or 2x speed though :). There are a lot of lectures, you can skip to the ones you're interested in.

If you just want some visual intuition behind eigen values and eigen vectors there's a very good blog post:
Eigen Vectors and Eigen Values explained visually
where the authors have dynamic visualizations. It's super fun to move things around and observe the effects.

There are lots of applications of linear algebra:
- Pagerank, the algorithm behind Google's success is based on eigen values and eigen vectors
- the winning entry in the Netflix Prize was based on Singular Value Decomposition
- 3D games use matrix multiplications for computing rotations, translations, shearing transforms
- in machine learning figuring out if the function you are learning is well conditioned for Gradient Descent corresponds to having a small ratio between the min and max eigen value of the hessian matrix
- again in machine learning figuring out if you're in a saddle point, local minima or local maxima can be done by looking at the signs of the eigen values of the hessian in the current point
- and of course they are sometime used in coding contest competitions :) (fast matrix exponentation, gaussian elimination etc)

Have fun!

CONCURSUL infO(1) CUP

Centrul Judeţean de Excelenţă Prahova lansează concursul "infO(1) CUP"!

Adresat tuturor elevilor si studenţilor pasionaţi de informatică, acesta presupune rezolvarea a 4-5 probleme de natură algoritmică pe parcursul a 5 ore. Întrucât se apropie Olimpiada Naţională de Informatică, considerăm că problemele pe care le propunem reprezintă un bun antrenament, dar şi o modalitate eficientă de a vă verifica cunostinţele în materie de algoritmică.

Aflându-se la prima ediţie, competiţia va avea numai o variantă online, însă sperăm ca, începând de anul următor, să organizăm şi o editie on-site! De remarcat faptul că proiectul este realizat în parteneriat cu Centrele Judeţene de Excelenţă din Olt, Neamţ, Sălaj, Satu Mare, Iaşi, Braşov şi Colegiul Naţional “Ion Luca Caragiale” Ploieşti.

Concursul constă în două runde:
Runda Naţională se va desfăşura pe 8 aprilie 2017 şi este adresată elevilor şcolarizaţi în Centrele Judeţene de Excelenţă din Romania. Din punctul de vedere al dificultăţii, această rundă este comparabilă unei runde Codeforces Div 2.
Runda Internaţională va avea loc pe 9 aprilie 2017 şi beneficiază de participarea unor echipe reprezentative din Bulgaria, Rusia, Republica Moldova, Serbia, Ungaria, Croaţia, Iran, Siria si Kazahstan.

Comisia ştiinţifică şi comisia tehnică sunt formate din elevi olimpici medaliaţi la Olimpiada Naţională şi Internaţională de Informatică şi absolvenţi ai unor prestigioase universităţi din lume.

Concursul va avea disponibilă şi o variantă online mirror. Înregistrarea este disponibilă pe site-ul concursului, prin intermediul form-ului de register înscriindu-vă la ambele probe. Variantele online mirror corespunzătoare celor două runde pot fi incepute sâmbătă, respectiv duminică, de la ora 15:00, participanţii alegându-şi un time frame de 5 ore în care pot simula concursul. Acestea sunt disponibile până duminică, ora 7:00, respectiv până miercuri, ora 15:00.
Informaţii suplimentare sunt disponibile pe site-ul competiţiei si pe blog-ul scris de Oncescu Costin •geniucos pe Codeforces.

Mulţumim sponsorilor noştri şi tuturor celor care ne-au fost alături! De asemenea, le dorim mult succes participanţilor!

Dupa doua editii in care initiativa unor elevi de la Colegiul National "Spiru Haret" din capitala a fost implementata cu succes, fiind sprijinita de conducerea liceului dar si de suportul material oferit de companii precum eMAG sau Siveco Romania, Concursul National de Informatica "Adolescent Grigore Moisil" revine cu cea de-a treia editie!

Avand un format de tip ACM-ICPC si adresandu-se tuturor elevilor din Romania, A.G.M incearca an de an sa reuneasca la Bucuresti elevi din cat mai multe judete ale tarii si sa creeze o atmosfera care sa ii incurajeze pe acestia sa se autodepaseasca pentru a reusi sa obtina un loc fruntas in cadrul competitiei.

Ca in fiecare an, initiativei noastre se alatura si persoane care nu au avut neaaparat vreo tangenta cu Colegiul National "Spiru Haret", dar care isi doresc ca prin sprijinul lor sa incurajeze toate persoanele din comunitate sa contribuie intr-un fel sau altul la buna dezvoltare a elevilor pasionati de informatica din Romania. Tin sa le multumesc tuturor acestor persoane si am sa incerc sa ii nominalizez pe toti cei care fac parte din aceasta categorie nu tocmai restransa :

- Echipa Infoarena, care ne-au sustinut inca de la prima editie si care prin ajutorul oferit si anul acesta raman un invariant atunci cand ne referim la A.G.M
- Florin Elfus •florin.elfus, Chichirim George •george_stelian, Ionescu Teodor •teoionescu si George Marcus •PlayLikeNeverB4 . Impreuna cu ei, am reusit sa creez nucleul comisiei stiintifice, care s-a mentinut inca de la prima editie a concursului. De asemenea, ei reprezinta un exemplu foarte bun cand vine vorba de notiunea de "invariant".
- Fundatia eMAG , care ne-a sarit pentru al doilea an la rand cu un ajutor financiar si care, prin contributia sa, ne-a facut sa fim optimisti cu privire la faptul ca cea de-a treia editie se va desfasura in conditii cel putin la fel de bune ca a doua.
- Atooom Industry and Resources SRL , un nume complet nou pentru unii, destul de familiar pentru altii. Start-up-ul la care doi dintre cei sase membrii ai comisiei stiintifice lucreaza (in speta, eu si cu Teodor Ionescu) va contribui intr-un mod mai putin obisnuit la premierea participantilor : in functie de rezultatele obtinute la concurs, un numar limitat de participanti din top va avea ocazia sa lucreze pe perioada verii in cadrul unui stagiu de practica in firma, dand piept cu un tip diferit de programare fata de cea competitiva.

Chiar daca au fost mai putin vizibili de-a lungul primelor doua editii si nu fac parte din categoria de mai sus (majoritatea fiind elevi la Colegiul National "Spiru Haret" din capitala), tin sa felicit intreaga echipa organizatorica a A.G.M pentru munca depusa in vederea organizarii concursului in conditii optime.

Dupa cum bine stiti, inscrierile pentru elevii din afara Bucurestiului se vor incheia pe 20 martie la ora 23:59. Din fericire pentru cei care nu au apucat sa se inscrie, s-a decis prelungirea termenului cu inca doua zile, astfel ca acestia mai au dreptul sa se inscrie pana la data de 22 martie, ora 23:59. Participantii din Bucuresti pot efectua inscrierea completand formularul de inscriere incepand cu data de 21 martie, ora 00:00. In apropierea concursului, site-ul oficial al competitiei si pagina oficiala de Facebook vor fi in permanenta actualizate cu ultimele informatii.

Inchei prin a spune ca dincolo de aceste persoane minunate pe care le-am nominalizat si care au sprijinit concursul, responsabili de o mare parte din succesul pe care acesta l-a avut sunteti voi: comunitatea Infoarena.

Keep coding!

Avem plăcerea de a da start-ul celei de-a patra ediţii a concursului de algoritmică MindCoding, ce se adresează tuturor celor pasionaţi de algoritmi şi arta programării, care îşi doresc îmbunătăţirea performanţelor şi a abilităţilor tehnice, dar şi să îşi extindă orizonturile spre adevărata industrie a programării.

MindCoding este structurat în 4 runde online şi o etapă finală, ce va avea loc în municipiul Cluj-Napoca, România, în perioada 28 - 30 aprilie 2017.

După prima ediţie, site-ul competiţiei a devenit o platformă educaţională, unde programatorii pasionaţi, indiferent de vârstă, îşi împărtăşesc rezultatele cercetărilor şi soluţiile la probleme cu întreaga noastră comunitate, care a atins peste 2500 de prieteni pe reţelele de socializare datorită implicării noastre continue.

În această nouă ediţie, concursul constă în rezolvare de probleme, ce implică îmbinarea algoritmilor cu aplicaţiile lor în viaţa reală. Mai mult, ediţia a 4-a aduce în întâmpinarea candidaţilor o nouă posibilitate: candidaţii pot alege să participe la divizia 2, unde, în comparaţie cu divizia 1, problemele vor avea un grad de dificultate mai scăzut. Scorul obţinut în divizia a doua nu va reprezenta un criteriu de calificare pentru runda finală, dar încurajăm participarea în număr cât mai mare indiferent de experienţa curentă şi participarea în divizia 1 în rundele următoare, în lupta pentru locul meritat în finală.

Fiecare rundă online se desfăşoară pe parcursul a 90 de minute, suficiente pentru rezolvarea a 4 probleme de algoritmică. Fiecărei probleme i se asociază la început un punctaj între 100 şi 1000, care scade odată cu trecerea timpului. Alegerea strategiei potrivite şi entuziasmul pot fi cheia pentru transformarea experienţei algoritmilor într-una remarcabilă.

Scorul total obţinut pentru calificarea în finală va fi calculat ca suma punctajelor obţinute de fiecare participant în toate rundele la care au participat în divizia 1. Următoarele categorii de participanţi vor ocupa locuri în finală: 15 concurenţi absolvenţi de liceu care nu locuiesc în Cluj-Napoca, 5 elevi din afara oraşului Cluj-Napoca, 20 de concurenţi absolvenţi de liceu din Cluj-Napoca, 10 elevi din Cluj-Napoca şi 5 concurenţi internaţionali.

După cele patru runde de calificare şi cele două runde finale, cei mai talentaţi şi vigilenţi participanţi vor fi recompensaţi cu 10 premii consistente, în bani.

Cu ocazia ultimei etape organizate la Cluj-Napoca, concurenţilor le va fi răsplătit efortul cu premii generoase, oferite de companii cunoscute precum eMAG, Bitdefender, Bosch şi TakeoffLabs. De asemenea, în atenţia participanţilor vor fi ofertele de job sau internship, interacţiunile cu participanţi la etapa internaţională a olimpiadei de informatică şi nu numai.

Le urăm mult succes participanţilor şi ne bucurăm să ne întâlnim şi în 2017 în comunitatea MindCoding!

Here's a fun question from Marius Dumitran.

Website visit counter: Given n log lines from a website, design a datastructure that can answer count_distinct queries efficiently. Log lines are given in sorted order and contain a timestamp (int64) and a user_id (int_64). count_distinct queries have a two int64 parameters: start_time and end_time. For each query you have to return the number of distinct users that have visited the website in the time range [start_time, end_time].

For example given the log lines
(0, 1)
(1, 2)
(2, 2)
(3, 1)
(4, 3)
(5, 1)
(6, 2)
(7, 3)
And the query count_distinct(1, 5), you should return 3, since we have user 2 visiting twice in that time range, user 1 visiting twice as well and user 3 visiting only once.

Catalysts Coding Contest este un concurs popular printre programatorii romani. Anul acesta, pentru prima data, se va desfasura si in Bucuresti, in cadrul Facultatii de Matematica si Informatica a Universitatii Bucuresti. In continuare va redam mesajul organizatorilor. Spor la treaba!

Dear Coder!

On 31 March 2017 the Catalysts Coding Contest (CCC) is coming to Bucharest!

The CCC is the largest programming competition in the German-speaking countries and among the Top 10 across Europe. This year the contest will be organized on an international level in several host cities in Germany, Spain, Belgium, Austria, France, South Africa, Nepal.

The University of Bucharest will be one of the Romanian hosts of the contest.

Whether it is C++, Java, .NET, JavaScript, Smalltalk, MATLAB or Excel - with us, everything is allowed, the target (an algorithm organized on 7 levels) is given, the path (any programming language you prefer) is left to everyone.

Prepare yourself for an exciting afternoon where you´ll meet a lot of people who share your passion. Make some noise at the contest and show us that you‘re up for the challenge!

Where: Str. Academiei 14, Sector 1, 010014, Bucharest – Faculty of Mathematics and Informatics

When: Friday, March 31, 15:00 - 19:00

PLEASE BRING YOUR OWN LAPTOP!

Usefull information about the competition:
- You have to register online first, before participating. Register here for both the CCC and the Online School CCC.
- You can participate individually or in teams of 2 or 3 people.
- You will use your own, personal laptop ; every team will only use one laptop.
- On our website you will find the Catcoder Platform for practicing with many examples of past contests.
- In the Hall of Fame you can compare your results with the best programmers of the last years

We are very pleased to welcome you at the CCC!*