Revizia anterioară Revizia următoare
Solutii Autumn WarmUp 2019
Problema Sec
Nu exista inca...
Solutia Problemei Rogvaiv
Solutia este prezentata de unul din concurenti,
Solutia 1
Vom rezolva problema prin metoda programării dinamice.
Fie ![d[i][j][k] d[i][j][k]](http://www.infoarena.ro/static/images/latex/cfda7589ada28adc71380b9ddd701354_3.5pt.gif) numărul de şiruri de lungime
numărul de şiruri de lungime 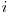 care au pe ultima poziţie al
care au pe ultima poziţie al 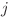 -lea caracter şi care conţin deja sau nu şirul
-lea caracter şi care conţin deja sau nu şirul 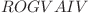 sau
sau 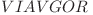 în funcţie de cerinţă.
în funcţie de cerinţă.
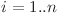
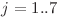 (considerăm primul </tex>V</tex> diferit de al doilea
(considerăm primul </tex>V</tex> diferit de al doilea 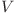 )
)
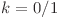 (
(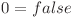 ,
, 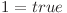 )
)
Pentru cerinţa 1.
Observăm că putem să punem pe ultima poziţie orice caracter din primele 6 fără a forma 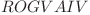 .
.
Deci ![d[i][j][k] d[i][j][k]](http://www.infoarena.ro/static/images/latex/5f6e8dbfd0e206d9d5a03ab309b43b96_3.5pt.gif) =
= ![d[i - 1][j][k] d[i - 1][j][k]](http://www.infoarena.ro/static/images/latex/f34a6320189e0542cd577469404e2787_3.5pt.gif) (
(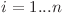 ,
, 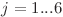 ,
, 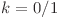 )
)
Pentru 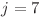 pot să formez şirul
pot să formez şirul 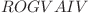 .
.
![d[i][7][1] = d[i][7][1] =](http://www.infoarena.ro/static/images/latex/93c310e1672541fafb12666549ab5bba_3.5pt.gif)
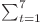
![d[i - 1][t][1] + d[i - 6][1][0] d[i - 1][t][1] + d[i - 6][1][0]](http://www.infoarena.ro/static/images/latex/250ec2618ed2bacc854e335b22424a78_3.5pt.gif) .
.
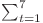
![d[i - 1][t][1] d[i - 1][t][1]](http://www.infoarena.ro/static/images/latex/2067335d224b72542cd35b459d36bfc0_3.5pt.gif) reprezintă toate şirurile care conţin deja şirul
reprezintă toate şirurile care conţin deja şirul 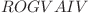 , iar
, iar ![d[i - 6][1][0] d[i - 6][1][0]](http://www.infoarena.ro/static/images/latex/9dd4694c5975f8be762aa4435ea8b867_3.5pt.gif) reprezintă numărul de subşiruri care au caracterul
reprezintă numărul de subşiruri care au caracterul 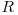 pe prima poziţie şi nu conţin deja şirul dat. Deci pe poziţiile rămase voi completa cu caracterele necesare pentru a forma
pe prima poziţie şi nu conţin deja şirul dat. Deci pe poziţiile rămase voi completa cu caracterele necesare pentru a forma 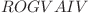 .
.
![d[i][7][0] d[i][7][0]](http://www.infoarena.ro/static/images/latex/8b71364d981f035d4f02cbd0ef573e8c_3.5pt.gif) =
= 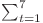
![d[i - 1][t][0] - d[i - 6][1][0] d[i - 1][t][0] - d[i - 6][1][0]](http://www.infoarena.ro/static/images/latex/414d53e8b6031f9a568645ee2cfeaf6f_3.5pt.gif) (scad cazurile în care se formează
(scad cazurile în care se formează 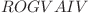 ).
).
Pentru cerinţa 2.
Recurenţa este asemănătoare.
De data aceasta doar caracterele cu indicii 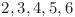 nu pot forma
nu pot forma 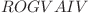 sau
sau 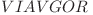 .
.
Deci ![d[i][j][k] = d[i - 1][j][k] d[i][j][k] = d[i - 1][j][k]](http://www.infoarena.ro/static/images/latex/f72a0fc06bc6b60169bc2addac7b61fc_3.5pt.gif) (
(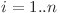 ,
, 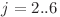 ,
, 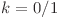 )
)
Cazul 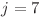 este identic cu cel de la cerinţa 1.
este identic cu cel de la cerinţa 1.
Pentru 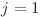 recurenţa devine:
recurenţa devine:
![d[i][1][1] = d[i][1][1] =](http://www.infoarena.ro/static/images/latex/e9c7bd672a560c839a8097616a37f0e3_3.5pt.gif)
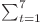
![d[i - 1][t][1] + d[i - 6][7][0] d[i - 1][t][1] + d[i - 6][7][0]](http://www.infoarena.ro/static/images/latex/c1b61a18646b8f88586f5ea76a703e3a_3.5pt.gif)
![d[i][1][0] = d[i][1][0] =](http://www.infoarena.ro/static/images/latex/8596add565c98f3192b6f6c163a10d5c_3.5pt.gif)
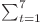
![d[i - 1][t][0] - d[i - 6][7][0] d[i - 1][t][0] - d[i - 6][7][0]](http://www.infoarena.ro/static/images/latex/f06a8a592dbef981b043cf1944e00d90_3.5pt.gif)
Rezultatul şi complexitatea.
Rezultatul este 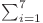
![dp[n][i][1] dp[n][i][1]](http://www.infoarena.ro/static/images/latex/8b35b5def5eedb33433d70f98de59fa0_3.5pt.gif) .
.
Complexitatea este 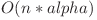 .
.
Solutia 2.
Considerăm următoarele stări:
Starea 1 = 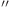 (nu conţine niciun caracter)
(nu conţine niciun caracter)
Starea 2 = 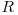
Starea 3 = 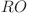
.
.
Starea 7 = 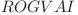
Astfel putem să ne folosim de dinamica ![d[i][j][k] d[i][j][k]](http://www.infoarena.ro/static/images/latex/a9e24b69d50e16a8031de5035c0140f2_3.5pt.gif) = numărul de şiruri de lungime
= numărul de şiruri de lungime 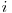 care se află în starea
care se află în starea 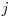 şi care conţin deja sau nu unul din şirurile date.
şi care conţin deja sau nu unul din şirurile date.
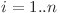
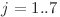
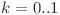
Pentru cerinţa 1.
La adăugarea unui caracter nou observăm că ori transformă starea 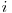 în starea
în starea 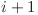 ori îl aduce la starea 1. Când se formeaza
ori îl aduce la starea 1. Când se formeaza 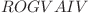
 devine 1 şi starea devine 0 (
devine 1 şi starea devine 0 (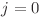 ).
).
Pentru cerinta 2.
Adăugăm încă 7 stări care corespund şirului inversat (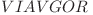 ), iar recurenţa este la fel.
), iar recurenţa este la fel.
Starea 8: 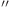
Starea 9: 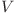
Starea 10: 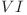
.
.
Starea 14: 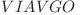
Răspunsul şi complexitatea.
Răspunsul este 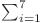
![d[n][i][1] d[n][i][1]](http://www.infoarena.ro/static/images/latex/9efdffa89443e99d444bed06f341289f_3.5pt.gif) .
.
Complexitatea este 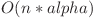
O optimizare care nu era necesară pentru a obţine punctaj maxim.
Menţionez că soluţia a doua poate fi îmbunătăţită.
Dacă liniarizăm dinamica putem să formăm o matrice care ridicată la puterea 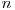 conţine valorile din care este format rezultatul.
conţine valorile din care este format rezultatul.
Astfel complexitatea devine 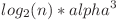 .
.
Soluţia problemei Shoturi
Solutia este prezentata de unul din concurenti,
Soluţie backtracking - 10 puncte
Generăm toate variantele posibile ale vectorului  pentru care
pentru care ![x[1] + x[2] + ... + x[N] = K x[1] + x[2] + ... + x[N] = K](http://www.infoarena.ro/static/images/latex/506d3abf4add17c6f8d9d61040f832f4_3.5pt.gif) . Această soluţie obţine 0 sau 10 puncte în funcţie de implementarea backtrackingului, care ar avea complexitatea
. Această soluţie obţine 0 sau 10 puncte în funcţie de implementarea backtrackingului, care ar avea complexitatea 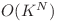 amortizat
amortizat
Soluţie N*K2 - 50 de puncte
Această soluţie presupune tehnica programării dinamice. Vom folosi matricea dp[n][k], pentru care:
- dp[i][j] = suma potenţelor tuturor amestecurilor posibile ingerând j
shoturipăhărele din primele isubstanţe interzisesucuri
De aici deducem recurenţa: ![\displaystyle \ dp[i][j]=\sum_{x=0}^{j-1} dp[i-1][x]*(j-x)*hazard[i] + dp[i-1][j] \displaystyle \ dp[i][j]=\sum_{x=0}^{j-1} dp[i-1][x]*(j-x)*hazard[i] + dp[i-1][j]](http://www.infoarena.ro/static/images/latex/350bc00be9751338c5f93cd121fb40d3_13.67783pt.gif)
De ce? Pentru că, din cum am definit dinamica, dp[i-1][x] = suma potenţelor tuturor amestecurilor posibile ingerând x păhărele din primele i-1 sucuri. Cum dp[i][j] presupune ingerarea a j pahare => se vor ingera j-x pahare de tipul i, care vor inmulţi fiecare potenţă cu ![(j-x)*hazard[i] (j-x)*hazard[i]](http://www.infoarena.ro/static/images/latex/0033c42641a5acba6e1599c5e7199a94_3.5pt.gif) . Adunăm dp[i-1][j] la dp[i][j] deoarece tinerii pot alege să nu bea niciun shot din cazanul i.
. Adunăm dp[i-1][j] la dp[i][j] deoarece tinerii pot alege să nu bea niciun shot din cazanul i.
Observatie: ![$dp[i][0]=1$ $dp[i][0]=1$](http://www.infoarena.ro/static/images/latex/bfe19fe89d285f60d71e66f929ceebec_3.5pt.gif) ,
, 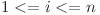 , ca să ne iasă calculele :)
, ca să ne iasă calculele :)
Voi exemplifica explicaţia cu cod în limbajul C++
dp[1][0]=1;
for(j=1; j<=k; j++)
dp[1][j]=(1LL*j*hazard[1])%MOD;
for(i=2; i<=n; i++)
{
dp[i][0]=1;
for(j=1; j<=k; j++)
{
for(x=0; x<=j-1; x++)
dp[i][j]=(dp[i][j]+1LL*dp[i-1][x]*(j-x)*hazard[i])%MOD;
dp[i][j]=(dp[i][j]+dp[i-1][j])%MOD;
}
}Obs: MOD=269 696 969 Nice
Solutie N*K, memorie N*K - 80 de puncte
Trecerea de la O(N*K2) la O(N*K) se face cu ajutorul sumelor parţiale.
Observăm că, dacă atunci când parcurgem cu j-ul ţinem o variabilă suma = ![\displaystyle \ \sum_{x=0}^{j-1} dp[i-1][x] \displaystyle \ \sum_{x=0}^{j-1} dp[i-1][x]](http://www.infoarena.ro/static/images/latex/497f6179355563d151c9cc06c568ca39_13.67783pt.gif) pe care o updatăm adăugând
pe care o updatăm adăugând ![dp[i-1][j] dp[i-1][j]](http://www.infoarena.ro/static/images/latex/1981cb1aafff8b6938e974f37b43f8b0_3.5pt.gif) şi o variabila suma_de_suma pe care o updatăm cu suma, acestea vor arata aşa:
şi o variabila suma_de_suma pe care o updatăm cu suma, acestea vor arata aşa:
| j | suma | suma_de_suma |
|---|---|---|
| 1 | 1*dp[i-1][0]1*dp[i-1][j-1] | 1*dp[i-1][0]1*dp[i-1][j-1] |
| 2 | 1*dp[i-1][0]+1*dp[i-1][1]1*dp[i-1][j-2]+1*dp[i-1][j-1] | 2*dp[i-1][0]+1*dp[i-1][1]2*dp[i-1][j-2]+1*dp[i-1][j-1] |
| 3 | 1*dp[i-1][0]+1*dp[i-1][1]+1*dp[i-1][2]1*dp[i-1][j-3]+1*dp[i-1][j-2]+1*dp[i-1][j-1] | 3*dp[i-1][0]+2*dp[i-1][1]+1*dp[i-1][2]3*dp[i-1][j-3]+2*dp[i-1][j-2]+1*dp[i-1][j-1] |
Se observă că, inmulţind suma_de_suma cu ![hazard[i] hazard[i]](http://www.infoarena.ro/static/images/latex/8005549c2c1828f4f40d6d94dfa68ae0_3.5pt.gif) , obţinem rezlultatul pentru dp[i][j].
, obţinem rezlultatul pentru dp[i][j].
Cum suma şi suma_de_suma sunt calculate in timpul parcurgerii cu j, complexitatea este 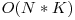
dp[1][0]=1;
for(i=1; i<=k; i++)
dp[1][i]=(1LL*i*hazard[1])%MOD;
for(i=2; i<=n; i++)
{
dp[i][0]=1;
suma=1;
suma_de_suma=1;
for(j=1; j<=k; j++)
{
dp[i][j]+=(1LL*suma_de_suma*hazard[i]+dp[i-1][j])%MOD;
suma=(suma+dp[i-1][j])%MOD;
suma_de_suma=(suma_de_suma+suma)%MOD;
}
}Soluţie N*K, memorie N - 100 de puncte
Deoarece pentru a calcula ![dp[i][ceva] dp[i][ceva]](http://www.infoarena.ro/static/images/latex/df42fd85b6be1d0e34ed35e5d7f426c0_3.5pt.gif) avem nevoie doar de
avem nevoie doar de ![dp[i-1][altceva] dp[i-1][altceva]](http://www.infoarena.ro/static/images/latex/c81007367c23eeb71adc73958d4f2f01_3.5pt.gif) , folosim doar 2 linii din matrice, de aceea putem să scăpăm de ea şi să păstrăm doar 2 vectori reprezentând ultimele 2 linii in ordinea parcurgerii. Astfel,
, folosim doar 2 linii din matrice, de aceea putem să scăpăm de ea şi să păstrăm doar 2 vectori reprezentând ultimele 2 linii in ordinea parcurgerii. Astfel, ![dp[j] dp[j]](http://www.infoarena.ro/static/images/latex/9a96dbccf71341082dd68c900a13960e_3.5pt.gif) va fi fostul
va fi fostul ![dp[i][j] dp[i][j]](http://www.infoarena.ro/static/images/latex/c35a5ee4b5fc770df50356fd1e333d59_3.5pt.gif) , iar
, iar ![aux[j] aux[j]](http://www.infoarena.ro/static/images/latex/8439505bb283899e0e0c67e6fd82fefb_3.5pt.gif) va fi fostul
va fi fostul ![dp[i-1][j] dp[i-1][j]](http://www.infoarena.ro/static/images/latex/1981cb1aafff8b6938e974f37b43f8b0_3.5pt.gif) . De aceea, memoria folosită este
. De aceea, memoria folosită este  în loc de
în loc de 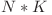 .
.
dp[0]=1;
for(i=1; i<=k; i++)
dp[i]=(1LL*i*hazard[1])%MOD;
for(i=2; i<=n; i++)
{
for(j=0; j<=k; j++)
aux[j]=dp[j];
dp[0]=1;
suma=1;
suma_de_suma=1;
for(j=1; j<=k; j++)
{
dp[j]=(1LL*suma_de_suma*hazard[i]+aux[j])%MOD;
suma=suma+aux[j];
if(suma>=MOD)
suma-=MOD;
suma_de_suma=suma_de_suma+suma;
if(suma_de_suma>=MOD)
suma_de_suma-=MOD;
}
}NOTA: Deoarece suma, suma_de_suma şi aux sunt deja 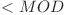 , adunarea lor va fi
, adunarea lor va fi 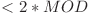 de aceea este necesar doar să scădem
de aceea este necesar doar să scădem 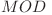 din ele când sunt
din ele când sunt 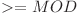 pentru a fi, din nou,
pentru a fi, din nou,