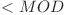Soluţia problemei Shoturi

Solutia este prezentata de unul din concurenti,

verde.cristian2005Verde Flaviu-Cristian
•verde.cristian2005

Soluţie backtracking - 10 puncte

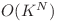Generăm toate variantele posibile ale vectorului x pentru care x[1] + x[2] + ... + x[N] = K. Această soluţie obţine 0 sau 10 puncte în funcţie de implementarea backtrackingului, care ar avea complexitatea O(K^N) amortizat

Soluţie N*K2 - 50 de puncte

Această soluţie presupune tehnica programării dinamice. Vom folosi matricea dp[n][k], pentru care:

  • dp[i][j] = suma potenţelor tuturor amestecurilor posibile ingerând j shoturi păhărele din primele i substanţe interzise sucuri

De aici deducem recurenţa: \displaystyle \ dp[i][j]=\sum_{x=0}^{j-1} dp[i-1][x]*(j-x)*hazard[i] + dp[i-1][j]

De ce? Pentru că, din cum am definit dinamica, dp[i-1][x] = suma potenţelor tuturor amestecurilor posibile ingerând x păhărele din primele i-1 sucuri. Cum dp[i][j] presupune ingerarea a j pahare => se vor ingera j-x pahare de tipul i, care vor inmulţi fiecare potenţă cu (j-x)*hazard[i]. Adunăm dp[i-1][j] la dp[i][j] deoarece tinerii pot alege să nu bea niciun shot din cazanul i.

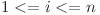Observatie: $dp[i][0]=1$, 1<=i<=n, ca să ne iasă calculele :)

Voi exemplifica explicaţia cu cod în limbajul C++

dp[1][0]=1;
    for(j=1; j<=k; j++)
        dp[1][j]=(1LL*j*hazard[1])%MOD;
    for(i=2; i<=n; i++)
    {
        dp[i][0]=1;
        for(j=1; j<=k; j++)
        {
            for(x=0; x<=j-1; x++)
                dp[i][j]=(dp[i][j]+1LL*dp[i-1][x]*(j-x)*hazard[i])%MOD;
            dp[i][j]=(dp[i][j]+dp[i-1][j])%MOD;
        }
    }

Obs: MOD=269 696 969 Nice

Solutie N*K, memorie N*K - 80 de puncte

Trecerea de la O(N*K2) la O(N*K) se face cu ajutorul sumelor parţiale.
Observăm că, dacă atunci când parcurgem cu j-ul ţinem o variabilă suma = \displaystyle \ \sum_{x=0}^{j-1} dp[i-1][x] pe care o updatăm adăugând dp[i-1][j] şi o variabila suma_de_suma pe care o updatăm cu suma, acestea vor arata aşa:

jsumasuma_de_suma
11*dp[i-1][0]
1*dp[i-1][j-1]		1*dp[i-1][0]
1*dp[i-1][j-1]
21*dp[i-1][0]+1*dp[i-1][1]
1*dp[i-1][j-2]+1*dp[i-1][j-1]		2*dp[i-1][0]+1*dp[i-1][1]
2*dp[i-1][j-2]+1*dp[i-1][j-1]
31*dp[i-1][0]+1*dp[i-1][1]+1*dp[i-1][2]
1*dp[i-1][j-3]+1*dp[i-1][j-2]+1*dp[i-1][j-1]		3*dp[i-1][0]+2*dp[i-1][1]+1*dp[i-1][2]
3*dp[i-1][j-3]+2*dp[i-1][j-2]+1*dp[i-1][j-1]

Se observă că, inmulţind suma_de_suma cu hazard[i], obţinem rezlultatul pentru dp[i][j].
Cum suma şi suma_de_suma sunt calculate in timpul parcurgerii cu j, complexitatea este 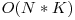O(N*K)

Cod c++
dp[1][0]=1;
    for(i=1; i<=k; i++)
        dp[1][i]=(1LL*i*hazard[1])%MOD;
    for(i=2; i<=n; i++)
    {
        dp[i][0]=1;
        suma=1;
        suma_de_suma=1;
        for(j=1; j<=k; j++)
        {
            dp[i][j]+=(1LL*suma_de_suma*hazard[i]+dp[i-1][j])%MOD;
            suma=(suma+dp[i-1][j])%MOD;
            suma_de_suma=(suma_de_suma+suma)%MOD;
        }
    }

Soluţie N*K, memorie N - 100 de puncte

Deoarece pentru a calcula dp[i][ceva] avem nevoie doar de dp[i-1][altceva], folosim doar 2 linii din matrice, de aceea putem să scăpăm de ea şi să păstrăm doar 2 vectori reprezentând ultimele 2 linii in ordinea parcurgerii. Astfel, dp[j] va fi fostul dp[i][j], iar aux[j] va fi fostul dp[i-1][j]. De aceea, memoria folosită este N în loc de N*K.

Cod c++
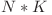dp[0]=1;
    for(i=1; i<=k; i++)
        dp[i]=(1LL*i*hazard[1])%MOD;
    for(i=2; i<=n; i++)
    {
        for(j=0; j<=k; j++)
            aux[j]=dp[j];
        dp[0]=1;
        suma=1;
        suma_de_suma=1;
        for(j=1; j<=k; j++)
        {
            dp[j]=(1LL*suma_de_suma*hazard[i]+aux[j])%MOD;
            suma=suma+aux[j];
            if(suma>=MOD)
                suma-=MOD;
            suma_de_suma=suma_de_suma+suma;
            if(suma_de_suma>=MOD)
                suma_de_suma-=MOD;
        }
    }

NOTA: Deoarece suma, suma_de_suma şi aux sunt deja 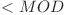<MOD, adunarea lor va fi 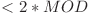<2*MOD de aceea este necesar doar să scădem 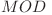MOD din ele când sunt 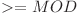>=MOD pentru a fi, din nou, <MOD