| Fişierul intrare/ieşire: | sdo.in, sdo.out | Sursă | Arhiva educationala |
| Autor | Arhiva Educationala | Adăugată de |  Andrei Misarca •Mishu91 |
| Timp execuţie pe test | 0.6 sec | Limită de memorie | 36864 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Poti vedea testele pentru aceasta problema accesand atasamentele.Vezi solutiile trimise | Statistici
Statistici de ordine
A i-a statistică de ordine a unei mulţimi este al i-lea cel mai mic element al mulţimi. Fiind date o mulţime de numere naturale M, de n elemente şi un număr natural k, să se determine a k-a statistică de ordine a mulţimii.
Date de intrare
Fişierul de intrare sdo.in conţine pe prima linie n şi k, iar pe a doua linie n numere naturale, reprezentând elementele mulţimii M.
Date de ieşire
În fişierul de ieşire sdo.out se va afla un singur număr natural, reprezentând a k-a statistică de ordine a mulţimii.
Restricţii
- 1 ≤ k ≤ n ≤ 3 000 000.
- Toate cele n elemente ale mulţimii M sunt din intervalul [1, 109].
Exemplu
| sdo.in | sdo.out |
|---|---|
| 8 3 1 10 4 13 7 6 11 14 | 6 |
Explicaţie
În exemplu, se observă că elementele aranjate în ordine crescătoare sunt: 1 4 6 7 10 11 13 14, prin urmare al 3-lea cel mai mic element este 6.
Indicaţii de rezolvare
Soluţia ce numără pentru fiecare element câte elemente sunt mai mici decât el, având complexitatea de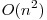 
, ar trebui să obţină 10 puncte.
Dacă modificăm algoritmul de sortare prin selecţie pentru a selecta cele mai mici k elemente, obţinem complexitatea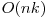 
. Această soluţie obţine în jur de 20 puncte.
Una din îmbunătăţiri constă în sortarea elementelor în complexitate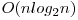 
şi selectarea valorii căutate în O(1). Soluţia ar trebui să obţină 50-60 puncte.
O altă soluţie, cu complexitatea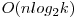 
, foloseşte un heap pentru a menţine cele mai mici k valori. Aceasta ar trebui să obţină 60 puncte, fiind o îmbunătăţire faţă de soluţia anterioară. În continuare, dacă construim un heap în complexitate 
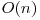iar pe acesta realizăm o parcurgere în lăţime ajungem la soluţia ce obţine acelaşi punctaj de complexitate 
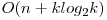. Deşi complexitatea este teoretic mai bună, ea se comportă mai slab decât cea menţionată anterior, datorită folosirii unei structuri de date ce încetineşte uşor, priority_queue.
O soluţie care foloseşte proprietatea că valorile sunt numere întregi, sortează elementele în timp liniar cu algoritmul radix sort. Această sursă ar trebui să obţină în jur de 70 de puncte. Motivele acestui punctaj constau în dimensiunea mare a datelor de intrare şi memoria suplimentară folosită.
Soluţia cea mai eficientă foloseşte funcţia de partiţionare a quicksort-ului pentru a determina a k-a statistică de ordine. Practic, acest algoritm este asemănător algoritmului Quicksort, cu deosebirea că se vor sorta doar anumite porţiuni care ajută la determinarea soluţiei. Însă, această soluţie obţine 90 de puncte. În sursa de 100 de puncte se va folosi un pivot ales aleator, în locul unui pivot fixat. Complexitatea acestui algoritm este în medie 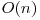, însă, teoretic, în cel mai defavorabil caz poate atinge 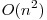pentru că am putea fi extrem de nenorocoşi să partiţionăm în jurul celui mai mare element rămas. Dar, deoarece algoritmul este aleator, nu există date de intrare particulare care să provoace comportamentul celui mai defavorabil caz. Iată motivul pentru care algoritmul ce selectează pivotul random este mai eficient decât cel care selectează un pivot fixat. Acest algoritm este implementat şi în STL: funcţia nth_element găsindu-se în headerul algorithm. O sursă demonstrativă se găseşte aici. Există şi un algoritm teoretic ce garantează 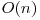pe cel mai defavorabil caz, şi se poate găsi în cartea „Introducere în algoritmi” la capitolul „10. Statistici de Ordine”.
