| Fişierul intrare/ieşire: | algsort.in, algsort.out | Sursă | Arhiva educationala |
| Autor | Arhiva Educationala | Adăugată de | |
| Timp execuţie pe test | 0.45 sec | Limită de memorie | 12288 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Sortare prin comparare
Se dau N numere naturale, intr-o ordine oarecare. Se pune problema sortarii lor in ordine crescatoare.
Date de intrare
Fisierul de intrare algsort.in va avea pe prima linie numarul N, iar pe a doua linie N numere naturale, separate prin cate un spatiu.
Date de iesire
In fisierul algsort.out veti tipari cele N numere din fisierul de intrare, sortate in ordine crescatoare.
Restrictii
- 1 ≤ N ≤ 500 000
- Toate cele N numere vor fi cuprinse intre 0 si 231-1 inclusiv.
Exemplu
| algsort.in | algsort.out |
|---|---|
| 6 4 1 7 5 1 3 | 1 1 3 4 5 7 |
Observatii
Limitele de timp si memorie folosite va ofera posibilitatea de a studia comparativ diverse implementari ale diversilor algoritmi de sortare intalniti.
In analiza comportamentului surselor evaluate trebuie sa tineti cont de faptul ca cea mai mare parte a timpului de executie va fi ocupata de citirea si scrierea datelor in fisier (pentru testele maxime, intre 400 si 600 ms vor fi ocupate de operatiile de intrare/iesire). Nu este necesara folosirea functiilor specializate de citire a blocurilor de caractere (parsarea citirii) pentru a obtine punctajul maxim, insa recomandam folosirea stream-urilor C++, care se comporta mai bine in mediul de evaluare decat functiile de citire din libraria standard C.
Structura testelor
Datorita largii varietati de algoritmi de sortare si comportarii lor diferite in functie de anumite particularitati structurale ale datelor de intrare, pentru evaluarea problemei se folosesc 5 grupe de cate 4 teste. Toate testele aflate in aceeasi grupa vor avea aceeasi valoare pentru N si acelasi domeniu de valori pentru cele N numere: ![0 \le v[i] \le \lfloor N \cdot \gamma \rfloor 0 \le v[i] \le \lfloor N \cdot \gamma \rfloor](http://www.infoarena.ro/static/images/latex/e9a880498a0bc23090c06d42a9b108e8_3.5pt.gif) , unde
, unde 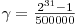 . Valorile lui N pentru cele 5 grupe de teste sunt 10, 1.000, 100.000, 350.000 respectiv 500.000. Testele din cadrul fiecarei grupe se vor diferentia astfel:
. Valorile lui N pentru cele 5 grupe de teste sunt 10, 1.000, 100.000, 350.000 respectiv 500.000. Testele din cadrul fiecarei grupe se vor diferentia astfel:
- primul test va contine numere generate aleator
- al doilea test va contine numere "aproape sortate" (numarul de inversiuni din lista de numere este mic)
- al treilea test va contine numerele sortate in ordine descrescatoare
- al patrulea test va contine numerele in ordine aleatoare, insa vor exista putine perechi de numere distincte (foarte multe dintre numere vor aparea de mai multe ori in fisierul de intrare)
Solutie
Structura problemei cere implementarea unui algoritm de sortare pe baza de comparatii. Exista, de asemenea, algoritmi de sortare care nu compara explicit elementele si care au performante mai bune pentru anumite cazuri particulare ale structurii datelor de intrare; acestia nu se preteaza insa cerintelor impuse in cazul de fata.
Orice algoritm de sortare bazat pe comparatii trebuie sa efectueze, pentru a putea distinge corect toate cele 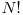 permutari posibile ale sirului de valori,
permutari posibile ale sirului de valori, 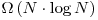 comparatii (o justificare a acestui rezultat se afla aici). Din aceasta perspectiva, algoritmi precum Merge Sort, Heapsort sau Introsort sunt optimi, executand
comparatii (o justificare a acestui rezultat se afla aici). Din aceasta perspectiva, algoritmi precum Merge Sort, Heapsort sau Introsort sunt optimi, executand 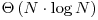 operatii in cazul cel mai defavorabil. Dintre acestia, Merge Sort foloseste
operatii in cazul cel mai defavorabil. Dintre acestia, Merge Sort foloseste 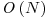 memorie suplimentara in implementarea clasica.
memorie suplimentara in implementarea clasica.
Un alt algoritm de sortare foarte popular este Quicksort. Desi complexitatea sa pentru cazul cel mai defavorabil este 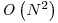 , in practica se comporta foarte bine si cunoaste multe imbunatatiri (detalii in prezentarea profesorului Robert Sedgewick aici si a profesorului Jon Bentley aici).
, in practica se comporta foarte bine si cunoaste multe imbunatatiri (detalii in prezentarea profesorului Robert Sedgewick aici si a profesorului Jon Bentley aici).
In libraria standard a limbajului C este implementata o varianta naiva de Quicksort (poate fi apelata prin qsort(...) - o sursa demonstrativa gasiti aici), iar STL-ul ofera programatorilor C++ atat functia sort, o implementare a algoritmului Introsort (o sursa demonstrativa aici), cat si functiile make_heap si sort_heap, pentru a putea implementa usor Heapsort (sursa demonstrativa aici). De asemenea, o varianta scurta de implementare a algoritmului Merge Sort (inspirata din acest articol) puteti gasi aici.
Alti algoritmi neoptimi, ce ruleaza in cazul mediu in complexitate 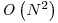 , dar elementari si foarte usor de inteles sunt: Bubblesort, Selection Sort si Insertion Sort.
, dar elementari si foarte usor de inteles sunt: Bubblesort, Selection Sort si Insertion Sort.
Pentru mai multe detalii si un studiu comparativ al algoritmilor de sortare vizitati pagina Wikipedia dedicata acestui subiect.
Aplicatii
Sortarea datelor apare ca subproblema sau etapa intermediara intr-o larga varietate de probleme si algoritmi, fiind considerata astfel una dintre temele principale de studiu in informatica teoretica. Diverse strategii greedy cu aplicatii in planificarea activitatilor, determinarea arborilor partiali de cost minim (algoritmul lui Kruskal) sau constructia codurilor Huffman, implica o prima etapa de sortare a datelor. De asemenea, in geometria computationala intalnim sortarea punctelor dupa unghiul polar pentru determinarea infasuratorii convexe sau metoda dreptei de baleiere, care presupune sortarea punctelor-eveniment dupa anumite criterii.
Alte probleme in care este folosita (intr-o forma sau alta) sortarea datelor:
- Loto
- Reactivi
- Akbardin’s Roads
- Granita
- Lungimi de interval
- Sport
- Rooks
- Cai
- Inversions
- Cutii
- Invsort
- Mexc
- Demolish
- Wolves and Sheep
- Antenna, CEOI 2006
- Sails, IOI 2007
 Poti vedea testele pentru aceasta problema accesand
Poti vedea testele pentru aceasta problema accesand 