Soluţii ONIS 2014, Runda 2
- Lista de probleme
- Pufarina
- Progr
- Progr2
- X si 0
- Heavytask
- Baruri
- ADN 2
- Facebook Search
- Pomi
- Fallingb
- Sireturi
Pufarina
Dacă procentajele ar fi numere naturale, un răspuns cu potenţial de a fi minim pentru orice set de intrare ar fi fost 100. Procentajele sunt numere reale însă, cu exact trei zecimale. Având acest lucru în vedere, pentru uşurinţa rezolvării problemei, vom transforma procentajele în numere naturale ≤ 100 000. Pentru acest lucru, se recomandă citirea fiecărui procentaj sub forma a două numere întregi x.y, procentajul după transformare fiind egal cu x * 1000 + y.
Astfel, suma tuturor procentajelor va fi egală cu 100 000. Putem deduce simplu că un răspuns cu potenţial de a fi minim este astfel 100 000. Se pune problema acum, dacă nu cumva există şi un număr mai mic decât acesta. Pentru a descoperi acest număr, va trebui să micşorăm procentajele, astfel încât raportul dintre ele să se păstreze. O modalitate de a face acest lucru este de a împărţi toate procentajele la un divizor comun al lor. Având în vedere că în final, vrem ca suma acestora să fie minimă, vom împărţi toate procentajele la cel mai mare divizor comun al lor. Numărul minim de votanţi va fi egal cu suma acestor procentaje. Dacă acest număr depaşeşte 50 000, votul este invalid.
Progr
Progresia aritmetică este unic determinată de primul termen şi raţia sa. Având în vedere că numerele pot lua valori până la 109, vom determina progresiile în functie de primii doi termeni conţinuti în acestea. Vom sorta numerele crescător, pentru că ne interesează doar progresiile cu raţie pozitivă. Vom seta termenul de start cu un indice i, iar cel de-al doilea termen cu un indice j. Pentru ca progresia care începe cu v[i] şi se termină cu v[j] să fie maximală, trebuie să verificăm existenţa unui număr x, cu proprietatea: x = v[i]-(v[j]-v[i]). Dacă acest număr x există în vector, progresia nu este maximală, deci nu o vom număra. Dacă nu există, o vom număra ca progresie maximală. Vom verifica existenţa acestui număr în vector folosind o tabelă hash.
Progr2
Asemănător ca la problema Progr, vom seta doi termeni consecutivi din cadrul unei progresii şi îl vom căuta pe un al treilea. Pentru afişarea răspunsului, ne vom ajuta de următoarea dinamică:
- d[i][j] = numărul de progresii care au ca ultimi doi termeni v[j] şi v[i], în această ordine.
Vom calcula această matrice astfel: Setăm indicele i, iar apoi setăm indicele j la stânga acestuia. Vom verifica existenţa unui număr v[k], k < j care are următoarea proprietate: v[k] = v[j]-(v[i]-v[j]).
- Dacă acest număr există, noi avem deja calculată valoarea din dinamică în d[j][k]. Deci, cum v[k] v[j] v[i] este o progresie, numărul de progresii care se termină cu v[j] şi v[i] este egal cu numărul de progresii care se termină cu v[k] şi v[j], la care se adaugă înca una, deci d[i][j] = d[j][k] + 1.
- Dacă acest număr nu există, singura progresie va fi chiar cea formată din v[j] şi v[i], deci d[i][j] = 1.
Existenţa acestui număr va fi verificată cu o tabelă hash, în care vom reţine pentru fiecare valoare poziţia pe care se află aceasta în vector. Rezultatul final va fi egal cu suma valorilor din această dinamică.
Heavytask
Putem sa ne gandim la solutie in felul urmator:
Descompunem numerele din sirul A in factori primi, si construim "imaginar" o matrice
- Exp[i][j] = exponentul celui de-al j-lea numar prim in descompunerea lui A[i]
Observam ca cmmmc al numerelor din A este produsul maximelor de pe coloane din matricea Exp.
Atunci pentru a obtine sirul B, noi trebuie sa modificam matricea Exp astfel incat maximul pe coloane sa nu se modifice, si toate valorile sa fie mai mici sau egale cu cele initiale. Astfel respectam cele doua conditii impuse pentru sirul B.
Acum, pentru a avea sirul B minim lexicografic, pastram un singur element per coloana din Exp egal cu maximul din acea coloana pentru sirul A, iar celelalte le setam la valoarea 0, iar in caz ca avem mai multi indici i pentru care Exp[i] pentru coloana curenta este maxim, il pastram doar pe cel mai mare, pentru a obtine sirul minim lexicografic.
Pentru rezolvarea problemei nu este necesara retinerea matricei Exp, ci doar pentru intelegerea solutiei. Operatiile descrise mai sus pot fi simulate cu GCD.
Baruri
Pentru a raspunde la intrebari, trebuia sa calculam suma tuturor elementelor dintre pozitiile B-D si B+D. Acum, nu putem calcula iterativ suma pentru fiecare din cele M intrebari, fiindca complexitatea ar fi O(N*M), unde N si M sunt foarte mari.
O prima abordare ar fi sa calculam sume partiale, astfel putand raspunde in O(1) la fiecare intrebare:
- sume[B + D] - sume[B - D - 1] - nr_prieteni[B].
Dar, la operatiile 1-3 trebuie sa modificam aceste sume partiale, ceea ce are o complexitate de O(N) pe update.
Solutia optima se foloseste de Arbori Indexati Binar, care au o complexitate de O(logN) atat pentru query, cat si pentru update. Un link care explica foarte bine aceasta structura de date este: Topcoder Binary Indexed Trees
ADN 2
Vom construi un automat finit ce va contine cele M secvente ADN (vezi Aho-Corasick). Vom nota cu Set(s) multimea secventelor ADN (din cele M) acceptate de starea s. Folosim metoda programari dinamice. Fie A[i][j][k] numarul de secvente ADN de lungime i, aflandu-ne la sfarsit in starea j si care sa contina ca subsecventa fiecare secventa ADN din multimea k (valoarea k fiind codificarea pe biti a unei submultimi a celor M secvente ADN). Daca avem calculate toate valorile A[i][j][k] pentru un i fixat, putem calcula valorile A[i + 1][j][k] astfel:
![A[i + 1][\delta_{j,c}][k \cup Set[\delta_{j,c}] += A[i][j][k], c \in \Sigma = \{A, C, G, T\} A[i + 1][\delta_{j,c}][k \cup Set[\delta_{j,c}] += A[i][j][k], c \in \Sigma = \{A, C, G, T\}](http://www.infoarena.ro/static/images/latex/a83dd115de36f3f9c23946a683f78bca_3.86108pt.gif) , unde
, unde 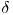 este functia de tranzitie a automatului.
este functia de tranzitie a automatului.
Constructia automatului are complexitatea 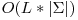 unde L reprezinta suma lungimilor celor M secvente ADN.
unde L reprezinta suma lungimilor celor M secvente ADN.
Calcularea tabloului A are complexitatea 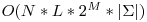 .
.
Facebook Search
Solutia se foloseste de structura de date numita Trie. Pentru fiecare nod din trie va mai trebui sa retinem nodul urmator cu relevanta maxima (a lui sau a fiilor lui), astfel incat daca se termina termenul introdus sa continuam cu nodul cel mai relevant.
Complexitate O(N + M * LUNG), unde LUNG = lungimea medie a cuvintelor introduse (~ 32)
Pomi
Problema se poate rezolva folosind programare dinamica.
In faza initiala se precalculeaza pentru fiecare pereche de tarusi/puncte (i, j):
- left[i][j] = numarul de pomi care se afla de partea 'stanga' a segmentului i-j, considerand directia de la i la j pentru a defini 'stanga'.
Pentru starea initiala la programare dinamica trebuie sa consideram un tarus I ca fiind parte din solutia optima. Vom alege toate posibilitatile pentru acest I, si apoi vom construi prin programare dinamica matricea min[i][j] cu semnificatia:
- min[i][k] = numarul minim de copaci care sunt in afara 'poligonului partial' obtinut din k-1 segmente cu capetele in multimea punctelor I, I + 1, I +2, ... i, dintre care s-au ales k puncte (=> k-1 segmente); printre care obligatoriu I si i.
Pentru recurenta iteram toate posibilitatile pentru capatul segmentului i (j de la I la i-1), si k de la 2 la P. Din toate posibilitatile vom alege pe cea care minimizeaza min[i][k], folosind left[i][j] calculat la pasul anterior.
Complexitate O(N2*M) + O(N3*P).
Fallingb
Problema se rezolva folosind programare dinamica.
Mai intai se observa ca orice rand din caroiaj poate fi reprezentat cu un numar de la 0 la 255 (deoarece randul are fix 8 pozitii si fiecare pozitie poate fi ocupata sau nu).
Ideea este sa retinem intr-un vector A[i][x] numarul de posibilitati (modulo 9901) de a umple un caroiaj de i + 1 linii astfel incat primele i linii sa fie complet umplute si pe ultima linie sa se gaseasca configuratia x.
De exemplu, pentru i = 3 si x = 00111111, A[i][x] reprezinta numarul de modalitati de a obtine urmatoarea figura: 00xxxxxx xxxxxxxx xxxxxxxx xxxxxxxx, unde 0 reprezinta o casuta libera si x o casuta ocupata.
Pentru a calcula A[i + 1][y] (pentru toate configuratiile y) in functie de A[i][x] (pentru toate configuratiile x), precalculam mai intai:
- B[x][y] = in cate moduri pot fi adaugate tipuri de forme pe linia cu configuratia x astfel incat linia (ce contine initial x) sa fie plina si imediat urmatoare sa aiba configuratia y.
De exemplu, pentru a ajunde de la x = 00xxxxxx la y = xx000000, exista trei modalitati:
- Se pun doua dreptunghiuri verticale (notate aa si respectiv bb)
ab000000 abxxxxxx
- Se pun un patrat (notat b) si un triunghi (notat aaa) (in doua moduri):
aa000000
baxxxxxx
sau
aa000000
abxxxxxx
In concluzie, B[00xxxxxx][xx000000] = 3.
De notat ca cele trei modalitati de a ajunge de la 00xxxxxx la xx000000 nu include posibilitatile de a adauga 4 patratele sau de a adauga doua dreptunghiuri orizontale deoarece acestea nu se pun doar pe linia x (s-ar aseza piese pe linia y (cele doua patratele de sus, respectiv dreptunghiul orizontal de sus).
Matricea B se poate calcula folosind backtracking. Odata calculata matricea B, formula pentru A[i + 1][x] este:
- A[i + 1][x] = Sum_y A[i][y] * B[y][x] (modulo 9901)
(numarul de moduri de a umple complet i + 1 linii si configuratia x pe linia i + 2 = numarul de moduri de a umple complet i linii si configuratia y pe linia i + 1 inmultit cu numarul de moduri de a ajunge de la y la x).
Rezultatul se gaseste in A[ M ][ 0 ]. (M linii complete, configuratia vida pe linia M + 1).
Sireturi
Mai intai se observa ca exista ((n-1)!)2 moduri de a lega sireturile respectand cerintele problemei. Acesta formula se poate gasi folosind urmatorul rationament:
Fie 1 1' 2 2' ... n n' o numerotare a gaurilor. Incepem in 1 si observam ca exista (n-1) posibilitati (2', 3', ..., n') de a ajunge in partea dreapta a pantofului. Din partea dreapta, avem din nou (n-1) posibilati de revenire in stanga (nu avem voie sa revenim in pozitia 1 decat la sfarsit). Mai departe, avem (n-2) posibilitati de a ajunge din nou in dreapta si (n-2) spre stanga, etc. In concluzie, (n-1) * (n-1) * (n-2) * ... * (n-2) * ... * 1 * 1. Formula se poate gasi si folosind alte rationamente.
Acum nu mai avem decat sa calculam numarul de divizori ai lui ((n-1)!)2. Fie p1, p2, ..., pk toate numerele prime de la 1 la 7500 (se pot calcula de exemplu folosind Ciurul lui Eratosthenes). Se calculeaza apoi factorizarea tuturor numerelor de la 1 la 7500:
- f[ i ] = vectorul [a1, a2, ..., ak] astfel incat i = p1a1 * ... * pkak (i de 1 la 7500)
Folosind f[i], se poate calcula factorizarea in numere prime a lui n! ca fiind:
- f[ (n-1)!2 ] = (f[ 1 ] + f[ 2 ] + ... + f[ n-1 ]) * 2
Avand factorizarea lui ((n-1)!2): ((n-1)!2) = p1b1 * ... * pkbk, numarul de divizori este (b1 + 1) * ... * (bk + 1). Raspunsul probleme este chiar acest produs modulo 9901.
