Solutii Junior Challenge 2020
- Lista de probleme
- Aparate
- Heist
- Plangaciosi
- Nambartiori
- Papagali
- Shopping
Soluţia problemei Aparate
Subtask 1 (10 puncte) - Q ≤ 1.000
Putem simula direct toate operaţiile cu brute-force. La un update, luăm toate coloanele şi le rotim în O(N) cu k poziţii, iar la un query luăm toate elementele de pe linia k cu coloanele de la l până la r şi le facem suma. Complexitatea pe un query este O(M), iar complexitatea unui update este O(N * M), deci complexitatea totală o să fie O(Q * N * M) pe cel mai rău caz.
Subtask 2 (20 puncte) - M ≤ 1.000
Putem să nu facem rotaţiile fizice şi să ţinem minte pentru fiecare coloană cu câte poziţii a fost rotită în sus. Dacă o coloană c a fost rotită în sus cu k poziţii, ca să accesăm elementul de pe linia l, putem defapt să accesăm din matricea iniţială elementul de pe linia (l + k) % N şi coloana c (cu precizarea că în soluţie indexăm liniile şi coloanele de la 0, nu de la 1).
La un update trebuie doar să actualizăm pentru fiecare coloană cu câte poziţii am rotit-o în sus, iar la un query putem direct să facem suma elementelor cerute.
Astfel complexitatea unui update devine O(M), iar complexitatea unui query devine tot O(M). Astfel, complexitatea finală o să fie O(Q * M).
Subtask 3 (30 puncte) - N = 2
Dacă N = 2, atunci M ≤ 50.000. La acest subtask avem două soluţii.
Prima ar fi să folosim un arbore de intervale pentru a simula operaţiile. Pentru fiecare nod din arborele de intervale (care ţine minte date despre intervalul de coloane [l, r]), trebuie să ţinem minte suma elementelor de pe linia 1 cu coloanele din intervalul respectiv, suma elementelor de pe linia 2 cu coloanele din intervalul respectiv, şi un lazy care să ne spună dacă trebuie să interschimbăm cele două linii pe care îl propagăm in fiii nodului. Această soluţie va avea complexitatea O(Q * logM).
O altă soluţie mai uşor de implementat ar fi să grupăm coloanele în grupe de câte B coloane. La un update, dacă o grupă este complet inclusă în intervalul respectiv, putem să ţinem minte ca şi la subtaskul 2 o valoare care să ne spună cu cât am rotit toate acele coloane din grupa respectivă. Dacă o grupă de coloane este doar parţial inclusă într-un update, putem să rotim fizic (ca şi la subtaskul 1) coloanele care sunt afectate de operaţie. Pentru fiecare grupă trebuie să menţinem şi sumele elementelor de pe fiecare linie. Ca să răspundem la un query luăm toate grupele: dacă o grupă este total inclusă, putem să facem ca şi la subtaskul 2, să vedem care este poziţia adevărată a liniei pe care o vrem, altfel dacă o grupă este inclusa parţial, atunci putem să luăm cu brut elementele din query. Complexitatea pentru un update sau un query va fi O(B * N + M / B). Deoarece N = 2, complexitatea finală va fi O(Q * (B * N + M / B)). Dacă fixăm B = sqrt(M), vom obţine complexitatea finală O(Q * sqrt(M)).
Subtask 4 (40 puncte)
La momentul acesta avem foarte multe soluţii care se încadrează în limita de timp pe anumite clase de teste: soluţia de la subtaskul 2 merge bine pe testele cu M mic, dar iese din timp pe celălalte teste, prima soluţie de la subtaskul 3 merge pe teste cu M mare (dacă îl adaptăm să meargă pe teste cu N > 2 în complexitate O(Q * N * logM)), iar a doua soluţie de la subtaskul 3 merge bine pe testele cu M mare, dar merge prost pe teste cu M mic (asta dacă ne fixăm B la început ca şi o constantă, precum 300, 500 sau 420).
Putem să combinăm mai multe soluţii între ele pentru a obţine soluţii care să se încadreze în limita de timp.
Cum combinăm soluţiile între ele?
Dacă avem o complexitate de forma N * B + M / B, şi trebuie să ne alegem convenabil un B, cel mai eficient este să egalăm cei doi termeni şi să aflăm astfel B-ul. Astfel o să obţinem:
N * B = M / B <=>
B^2 = M / N => B = sqrt(M / N)
Varianta aceasta este optimă. Putem demonstra asta folosind inegalitatea mediilor care spune că (a + b) / 2 ≥ sqrt(a * b), iar egalitatea se obţine dacă a şi b sunt egale. Astfel, dacă înlocuim termenii cu expresia noastră iniţială, o să obţinem că (N * B + M / B) / 2 ≥ sqrt(N * M), deci (N * B + M / B) ≥ sqrt(N * M) care este o constantă. Deci dacă egalăm cei doi termeni (aşa cum am procedat mai sus), vom obţine complexitatea optimă.
Acuma putem să combinăm toate soluţiile între ele şi să vedem ce obţinem:
# Putem combina soluţia de la subtaskul 2 cu prima de la subtaskul 3
# Putem combina soluţia de la subtaskul 2 cu a doua de la subtaskul 3
Totuşi, din punct de vedere al implementării ar însemna să implementăm două soluţii independente şi ar ieşi mult mai greoi implementarea. În continuare vom analiza mai mult soluţia de la subtaskul 3.
Complexitatea soluţiei este O(Q * (N * B + M / B)). Dacă folosim formula de mai sus, vom obţine că B trebuie să fie sqrt(M / N). Complexitatea finală va fi O(Q * (N * sqrt(M / N) + M / sqrt(M / N))) = O(Q * sqrt(M * N)).
De menţionat că sqrt(M / N) poate fi mai mic decât 1. Cum nu putem fixa un bucket cu 0, putem folosi funcţia ceil() pentru a evita astfel de probleme. În cazul acesta, practic soluţia noastră care face mai multe bucketuri imită soluţia de la subtaskul 2.
Altă menţiune ar mai fi faptul că aici mărimea bucketului variază, şi este esenţial să avem grija de acest lucru şi să nu fixăm mărimea lui ca şi o constantă în cod.
Soluţia problemei Heist
Prima observaţie importantă este că 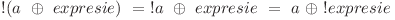 si ca
si ca 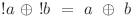 . Aşadar ne dăm seama că orice expresie poate fi rescrisă fără semne de negaţie sau cu un singur semn de negaţie, în funcţie de paritatea numărului semnelor de negaţie care apar în expresia iniţială.
. Aşadar ne dăm seama că orice expresie poate fi rescrisă fără semne de negaţie sau cu un singur semn de negaţie, în funcţie de paritatea numărului semnelor de negaţie care apar în expresia iniţială.
Cum operaţia xor e asociativă şi comutativă şi 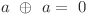 , putem scrie orice expresie fără paranteze şi fiecare variabilă să apară fie o dată, fie deloc. Astfel singurele expresii pe care trebuie să le luăm în considerare sunt cele cu maxim
, putem scrie orice expresie fără paranteze şi fiecare variabilă să apară fie o dată, fie deloc. Astfel singurele expresii pe care trebuie să le luăm în considerare sunt cele cu maxim  variabile în care putem avea maxim un semn de negaţie. În total sunt
variabile în care putem avea maxim un semn de negaţie. În total sunt 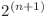 astfel de expresii deci dacă le-am genera pe toate şi le-am evalua cu un backtracking, complexitatea finală ar fi
astfel de expresii deci dacă le-am genera pe toate şi le-am evalua cu un backtracking, complexitatea finală ar fi 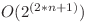 , o soluţie care dacă este suficient de bine optimizată poate să ia 60 de puncte.
, o soluţie care dacă este suficient de bine optimizată poate să ia 60 de puncte.
Ne dăm seama că dacă pe prima poziţie din şirul de biţi apare  , atunci semnul de negaţie apare neapărat. La fel dacă pe prima poziţie din şirul de biţi apare
, atunci semnul de negaţie apare neapărat. La fel dacă pe prima poziţie din şirul de biţi apare  , atunci nu avem semn de negaţie. Astfel putem determina în
, atunci nu avem semn de negaţie. Astfel putem determina în 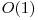 dacă avem negaţie sau nu. Dacă avem negaţie, putem nega întreg şirul de biţi şi putem rezolva problema la fel ca în cazul în care nu avem negaţie. Mai departe rezolvăm problema când nu avem negaţie.
dacă avem negaţie sau nu. Dacă avem negaţie, putem nega întreg şirul de biţi şi putem rezolva problema la fel ca în cazul în care nu avem negaţie. Mai departe rezolvăm problema când nu avem negaţie.
Dacă indexăm şirul de biţi de la  , ştim că bitul de pe poziţia
, ştim că bitul de pe poziţia 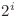 , unde
, unde 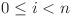 , îi corespunde valorii expresiei atunci când toate variabilele mai puţin variabila cu ordinul
, îi corespunde valorii expresiei atunci când toate variabilele mai puţin variabila cu ordinul 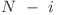 sunt egale cu
sunt egale cu  . Dacă bitul de pe poziţia
. Dacă bitul de pe poziţia 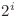 are valoarea
are valoarea  înseamnă că variabila nu apare în expresie, iar dacă are valoarea
înseamnă că variabila nu apare în expresie, iar dacă are valoarea  înseamnă că variabila apare în expresie. Astfel am determinat în
înseamnă că variabila apare în expresie. Astfel am determinat în 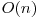 o expresie posibil validă. Trebuie să verificăm dacă expresia determinată este corecta, asta fiind foarte uşor cu un backtracking de complexitate
o expresie posibil validă. Trebuie să verificăm dacă expresia determinată este corecta, asta fiind foarte uşor cu un backtracking de complexitate 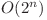 , soluţie care obţine 100 de puncte.
, soluţie care obţine 100 de puncte.
Soluţia problemei Plangaciosi
O primă observaţie este că pentru a rezolva problema trebuie să aflăm câte secvenţe de alegeri există pentru fiecare lungime posibilă.
Subtaskul 1
Când numărul de secvenţe posibile este cel mult 2 * 106, problema poate fi rezolvată prin backtracking, generând toate secvenţele posibile.
Subtaskul 2
Când Ai = 1, pentru orice i, numărul de secvenţe de alegeri de lungime L este combinari(N, L) * L.
Subtaskul 3
Putem fixa, pe rând, tortul din care şi-ar dori să manânce PlângăciosulNr1. Fie acesta tortul x.
Vom folosi programarea dinamică pentru a calcula dp[i][j] = în câte moduri putem alege j felii, considerând doar primele i torturi, astfel încât în fiecare tort să rămână un număr nenegativ de felii, iar din tortul x să nu fie luată nicio felie.
Recurenţa pentru i != x este: dp[i][j] = suma (dp[i-1][j-t] * combinari(j, t)), unde 0<=t<=a[i]
Recurenţa pentru i = x este: dp[i][j] = dp[i-1][j]
Apoi, putem calcula cnt[x][i] = câte secvenţe de alegeri se termină cu tortul x şi au lungimea i.
cnt[x][i] = dp[n][i - a[x]] * combinari(i, a[x]).
Obţinem complexitatea O(N * S2), unde S = sumă(Ai).
Subtaskul 4
Putem îmbunătăţi soluţia anterioară observând că dacă torturile x şi y au acelaşi număr de felii, atunci cnt[x][i] = cnt[y][i], pentru orice i. Astfel, putem rula dinamica anterioară câte o dată pentru fiecare valoare distinctă din A. În total, sunt cel mult sqtr(2*sum(Ai)) valori distincte. Obţinem complexitatea O(S2 * sqrt(S)).
Subtaskul 5
Vom construi o altă dinamică, D[i][j][0/1] = în câte moduri putem alege j felii, considerând doar primele i torturi, astfel încât în fiecare tort să rămână un număr nenegativ de felii. A treia dimensiune poate fi 0 sau 1, specificând dacă tortul din care şi-ar dori să manânce PlângăciosulNr1 se află între primele i torturi. Recurenţa este:
D[i][j][ 0 ] = suma (D[i-1][j-t ][ 0 ] * combinari(j, t)), unde 0<=t<=a[i]
D[i][j][ 1 ] = D[i-1][j-a[i]][ 0 ] * combinari(j, a[i]) + suma (D[i-1][j-t][ 1 ] * combinari(j, t)), unde 0<=t<=a[i]
Complexitatea acestei soluţii este O(S2).
Soluţia problemei Nambartiori
Notăm cu 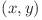 cel mai mic divizor comun dintre
cel mai mic divizor comun dintre  şi
şi 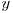 .
.  şi
şi  au semnificaţia din enunţ.
au semnificaţia din enunţ.
Cazul cu 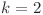 o sa îl tratăm separat. Se observă că orice două numere naturale
o sa îl tratăm separat. Se observă că orice două numere naturale 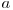 şi
şi 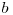 cu
cu 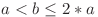 formează o progresie geometrică validă, deoarece
formează o progresie geometrică validă, deoarece 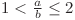 . Deci numărul de progresii geometrice care încep cu un număr
. Deci numărul de progresii geometrice care încep cu un număr 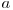 este chiar
este chiar 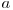 .
.
Fie 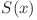 numărul de progresii geometrice de lungime
numărul de progresii geometrice de lungime 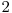 care încep cu un număr mai mic sau egal decât
care încep cu un număr mai mic sau egal decât  şi au raţia între
şi au raţia între  şi
şi 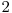 . Conform observaţiei de mai sus
. Conform observaţiei de mai sus 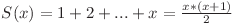 . Putem afla prima poziţie din progresia geometrică cu o căutare binară în
. Putem afla prima poziţie din progresia geometrică cu o căutare binară în 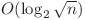 sau cu o parcurgere simplă în
sau cu o parcurgere simplă în 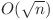 . Mai departe este foarte simplu să aflăm care este progresia cerută.
. Mai departe este foarte simplu să aflăm care este progresia cerută.
Fie 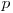 primul termen al unei progresii. Putem scrie raţia unei progresii ca
primul termen al unei progresii. Putem scrie raţia unei progresii ca 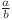 , unde
, unde 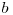 şi
şi 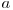 sunt numere naturale prime între ele astfel încât
sunt numere naturale prime între ele astfel încât 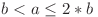 .
.
Avem 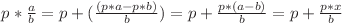 . Cum
. Cum 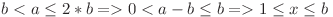
În loc de a afla numărul de fracţii 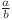 putem afla numărul de fracţii de forma
putem afla numărul de fracţii de forma 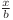 , cu
, cu 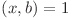 si
si 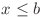 , pentru că sunt echivalente conform demonstraţiei de mai sus.
, pentru că sunt echivalente conform demonstraţiei de mai sus.
Dacă vrem ca progresia să aibă  termeni, atunci ne interesează fracţiile pentru care numărul
termeni, atunci ne interesează fracţiile pentru care numărul 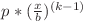 este număr natural. Cum
este număr natural. Cum 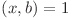 , proprietatea anterioară este echivalentă cu
, proprietatea anterioară este echivalentă cu 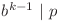 .
.
Rămâne să numărăm câte fracţii există. Pentru un 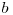 valid,
valid,  poate lua valori doar numere mai mici sau egale cu
poate lua valori doar numere mai mici sau egale cu 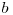 astfel încât
astfel încât 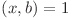 , deci numarul de fracţii este
, deci numarul de fracţii este 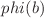 (Indicatorul lui Euler).
(Indicatorul lui Euler).
Fie 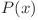 numărul de progresii geometrice de lungime
numărul de progresii geometrice de lungime  care încep cu
care încep cu  şi au raţia mai mare strict decât
şi au raţia mai mare strict decât  şi mai mică sau egală cu
şi mai mică sau egală cu 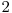 . Conform observaţiei de mai sus
. Conform observaţiei de mai sus 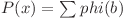 , unde
, unde 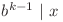 .
.
Fie 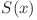 numărul de progresii geometrice de lungime
numărul de progresii geometrice de lungime  care încep cu un număr mai mic sau egal decât
care încep cu un număr mai mic sau egal decât  şi au raţia între
şi au raţia între  şi
şi 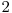 . Aşadar
. Aşadar 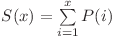 . Dacă extindem suma obţinem
. Dacă extindem suma obţinem 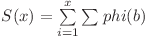 , unde
, unde 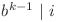 . Putem calcula suma rapid dacă aflăm pentru fiecare
. Putem calcula suma rapid dacă aflăm pentru fiecare 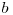 de câte ori apare
de câte ori apare 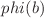 în sumă.
în sumă. 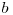 poate lua valori până la
poate lua valori până la ![\sqrt[k-1]x \sqrt[k-1]x](http://www.infoarena.ro/static/images/latex/535c3a8cd9f211a094688120c0e29273_3.39725pt.gif) , iar
, iar 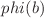 apare de
apare de 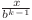 ori în sumă. Deci putem calcula
ori în sumă. Deci putem calcula 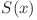 în
în ![O(\sqrt[k-1]x) O(\sqrt[k-1]x)](http://www.infoarena.ro/static/images/latex/32f4b99e7788b1b10a5145901621dbc1_3.5pt.gif) . Căutăm binar prima valoare din progresie. Fie aceasta
. Căutăm binar prima valoare din progresie. Fie aceasta 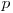 . Fie
. Fie 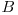 cel mai mare numar astfel încât
cel mai mare numar astfel încât 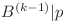 . Observăm că
. Observăm că 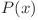 poate fi scris ca
poate fi scris ca 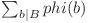 , dar această sumă este egală cu
, dar această sumă este egală cu 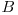 deoarece
deoarece 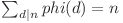 . Fie fracţiile
. Fie fracţiile 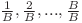 . Numărul acestora este
. Numărul acestora este 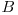 , ele fiind distincte două câte două, iar pentru că
, ele fiind distincte două câte două, iar pentru că 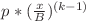 este natural, înseamnă că progresiile geometrice valide care încep cu p sunt doar cele care au raţiile egale cu
este natural, înseamnă că progresiile geometrice valide care încep cu p sunt doar cele care au raţiile egale cu 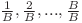 . Pe noi ne interesează
. Pe noi ne interesează 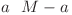 progresie geometrică care începe cu
progresie geometrică care începe cu 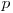 , unde
, unde 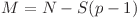 . Conform observaţiilor anterioare aceasta este
. Conform observaţiilor anterioare aceasta este 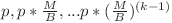 . Complexitatea finală pentru a afla
. Complexitatea finală pentru a afla 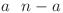 progresie geometrică de lungime
progresie geometrică de lungime  este
este ![O(\sqrt[k-1]n * \log_{2}n) O(\sqrt[k-1]n * \log_{2}n)](http://www.infoarena.ro/static/images/latex/31428f337e8b5a255e517e6ba8bf9244_3.5pt.gif) .
.
Soluţia problemei Papagali
O primă observaţie este că dacă avem x papagali dintr-o specie, atunci ei pot fi cuplaţi în (x-1) * (x-3) * (x-5) * ... * 1 moduri. Acest fapt este adevărat deoarece cel mai din stânga papagal poate fi cuplat cu oricare dintre ceilalţi N-1 papagali, apoi cel mai din stânga papagal necuplat încă poate fi cuplat cu oricare dintre ceilalţi N-3 papagali necuplaţi încă, şi tot aşa.
În ceea ce priveşte aşezarea papagalilor într-un şir, sunt Nr = comb(N, A1) * comb(N-A1, A2) * comb(N-A1-A2, A3) * ... * comb(AK, AK) moduri de a aşeza papagalii. Acest fapt poate fi justificat astfel: sunt comb(N, A1) moduri de a alege poziţiile pe care stau papagalii din prima specie, apoi sunt comb(N-A1, A2) moduri de a alege (dintre poziţiile neocupate încă) poziţiile pe care stau papagalii de a doua specie, şi tot aşa. Prin dezvoltarea combinărilor, obţinem Nr = N! / (A1! * A2! * ... * AK!).
Combinând cele două observaţii, obţinem că numărul de scheme de papagali este: S = N! / (A1!! * A2!! * ... * AK!!), unde x!! = x * (x-2) * ... * 2.
Dacă vrem să cumpărăm papagali noi, atunci vom cumpăra câte 2 papagali noi la fiecare pas şi vom precalcula răspunsurile pentru toate query-urile posibile. La fiecare pas trebuie să cumpărăm papagali dintr-o specie care conţine număr minim de papagali la momentul respectiv. Pentru a afla numărul minim de papagali dintr-o specie la un anumit pas, putem menţine un heap sau un vector de frecvenţa.
Soluţia problemei Shopping
Avem nevoie de două observaţii:
- Putem afla maximul dintre p[i] şi p[j] făcând un query între două stringuri A şi B unde B este plin de 'a'-uri, iar A este plin de 'a'-uri înafară de poziţiile i şi j care vor avea 'b'. Costul acestei operaţii va fi 2.
- Nu putem distinge în permutare elementele 1 şi 2. Totuşi, dacă aflăm celelalte elemente, atunci putem să spunem pe ce poziţie se află 1 şi pe ce poziţie se află 2.
Nota: De acum încolo, ne vom orienta după numărul de operaţii descrise mai sus, nu după suma costurilor stringurilor. De asemenea, definim funcţia queryMax(a, b) = max(p[i], p[j])
Subtaskul 1
La acest subtask merge orice soluţie de tip backtracking. Putem să facem nişte operaţii random ca după să încercăm să facem toate permutările şi să vedem care permutare corespunde cu operaţiile generate.
Subtaskul 2
La acest subtask putem să generăm maximul între oricare pereche de numere într-o matrice A[i][j] = max(P[i], P[j]). Ca să aflăm pe ce poziţie se află elementul maxim, trebuie să găsim linia sau coloana care este plină de maximul respectiv. După ce deducem că maximul se află pe poziţia i, excludem linia şi coloana i din matrice şi continuăm până când ajungem la o matrice 2×2.
Subtaskul 3
La această soluţie putem încerca orice soluţie ce foloseşte căutarea binară. Să zicem că noi am aflat pe poziţiile de la 1 până la x toate elementele şi ştim şi în ce ordine sunt. Pentru elementul x + 1 putem afla între care dintre elemente se află făcând comparaţii, astfel obţinem o soluţie cu O(N * logN) operaţii.
Subtaskul 4
Să zicem că avem două poziţii a şi b pentru care cunoaştem maximul şi, folosindu-ne de aceste informaţii, vrem să aflăm elementul de pe poziţia c, sau măcar să aflăm un element dintre a, b şi c. Putem să facem două query-uri ca să aflăm maximele între oricare două elemente. Vom avea 3 cazuri:
- queryMax(a, c) = queryMax(b, c) = x => pe poziţia c se află valoarea x. De acuma putem să îl ignorăm pe c şi să continuăm cu celelalte elemente.
- queryMax(a, b) = queryMax(a, c) = x => pe poziţia a se află valoarea x. De acuma putem să îl ignorăm pe a şi să continuăm cu celelalte elemente, numai că elementele pe care nu le ştim, dar le cunoaştem maximul vor fi b şi c.
- queryMax(a, b) = queryMax(b, c) = x => pe poziţia b se află valoarea x. Cazul acesta este analog cu cel anterior.
Astfel vom folosi exact 2 * N query-uri dacă avem grijă să nu facem operaţii care se repetă.
Subtask 5
În soluţia de mai sus, valorile de poziţiile a şi b vor deveni din ce în ce mai mici pe măsură ce se modifică a şi b. În particular, dacă am procesat toate elementele de pe poziţiile de la 1 pana la i, atunci a şi b se vor referi la cele mai mici două valori din permutare de pe prefixul respectiv.
Putem modifica soluţia de mai sus pentru a aplica query-uri într-un mod eficient.
- Dacă queryMax(a, b) < queryMax(b, c) = x => pe poziţia c se află elementul x, putem să îl ignorăm şi să continuăm cu celelalte elemente.
- Dacă queryMax(a, b) == queryMax(b, c) = x => pe poziţia b se află elementul x. Putem de acuma să îl ignorăm şi să continuăm cu celelalte elemente folosind a şi c. În cazul acesta va trebui să facem un query în plus pentru a afla queryMax(a, c)
- Dacă queryMax(a, b) > queryMax(b, c) = x => pe poziţia a se află elementul x. Putem de acuma să îl ignorăm şi să continuăm cu celelalte elemente folosind b şi c. În acest caz nu va trebui să facem un query în plus pentru a afla queryMax(b, c), deoarece îl cunoaştem deja, dar pentru a fi mai clar ce urmează, o să facem acel query, chiar dacă este degeaba.
Cum a şi b se vor schimba şi se vor referi la cele mai mici două elemente de pe prefix, cumva putem vedea că primul caz se va întâmpla din ce în ce mai mult. Dacă folosim această soluţie cu random_shuffle, numărul de operaţii folosite va fi pe medie N + 10, ceea ce se încadrează în limită şi va lua 100 de puncte.
Demonstraţie
Numărul de query-uri folosite va fi N + T unde T va fi numărul de dăţi în care schimbăm pe a şi b, care va fi defapt numărul de dăţi in care, dacă parcurgem o permutare de la stânga la dreapta, se schimbă cele mai mici două elemente.
Definim Exp[N] = numărul de dăţi în care se schimbă cele două minime dacă parcurgem permutarea de la stânga la dreapta pe medie. Astfel T va fi defapt Exp[N]. Ca să calculăm relaţia de recurenţă, trebuie să analizăm modul de construcţie al permutărilor. La o permutare de mărime N - 1 vom adăuga la sfârşit un element x, iar toate elementele din vechea permutare care sunt mai mari sau egale cu x vor creşte cu 1. Dacă x este 1, atunci numărul de dăţi în care cele două minime se schimbă va creşte cu 1 pe lângă numărul de dăţi pe care îl aveam în cadrul permutărilor de lungime 1. Dacă elementul adăugat va fi 2, atunci numărul de dăţi va creşte iarăşi cu 1 faţă de cele din permutările de lungime N - 1. Dacă elementul adăugat e de la 3 până la N, atunci numărul de schimbări ale celor două minime nu se schimbă. Astfel, relaţia de recurenţă va fi:
Exp[N] = (Exp[N - 1] + 1) * 1 / N + (Exp[N - 1] + 1) * 1 / N + Exp[N - 1] * (N - 2) / N <=>
Exp[N] = Exp[N - 1] + 2 / N
Dacă desfacem formula, vom obţine Exp[N] = 2 / 1 + 2 / 2 + ... + 2 / N = 2 * (1 / 1 + 1 / 2 + ... + 1 / N).
Suma 1 / 1 + 1 / 2 + ... + 1 / N poate fi la rândul ei aproximată cu logN. Aşadar, numărul de operaţii folosit va fi pe medie N + 2 * logN.
