Solutii Algoritmiada 2019, Runda PreONI

• Lista de probleme
• Chei
• ColorfulConflict
• Bazar

Solutia problemei Chei

In primul rand, pot distinge doua chei de forme diferite. Consideram cazul acesta acoperit in demonstratiile care urmeaza.

Intuitia

Ca sa pot distinge doua chei de aceeasi forma, am nevoie de un reper care nu se modifica atunci cand mi se roteste inelul in buzunar sau cand privesc sirul dintr-o alta parte. Un posibil reper ar fi sa consider o distanta d si sa compar perechea de chei aflate la distanta circulara d de prima cheie cu perechea de chei aflate la distanta circulara d de a doua cheie. Daca perechile neordonate ar fi distincte, cu siguranta pot distinge cheile.

Spre exemplu, in sirul de chei baxac, cheile de tip a au la distanta d = 1 perechile de chei (x, b) si (x, c).

Cu toate acestea, verificarea aceasta este insuficienta. De exemplu, pentru sirul bbaccbcabc, cheile a au perechea de chei (b, c) pentru toate distantele d (mai putin cand ambele obtin perechea (a, a)), dar pot sa le disting cu urmatorul rationament: Daca, in loc sa consider doar caracterul aflat la distanta d, as considera tot sirul de caractere pana la acel caracter? Practic, distanta d de o cheie nu ne mai da doar un caracter, ci intregul sir vizitat pana acolo.

Astfel, pentru sirul bbaccbcabc, cheile a au perechile de siruri de chei, pentru d = 2, ("bb", "cc"), respectiv ("cb", "bc"). Deci le putem distinge. Dar daca tot comparam perechi de siruri de marime d, nu mai bine comparam doar pentru d = N?

Concret

Sa notam cu alfa(p) sirul de N caractere pe care il citesc parcurgand circular spre dreapta sirul de chei incepand cu cea de la pozitia p.
Sa notam cu beta(p) sirul de N caractere pe care il citesc parcurgand circular spre stanga sirul de chei incepand cu cea de la pozitia p.

Lema

Pot distinge doua chei aflate la indicii p si q <=> multimea / perechea neordonata {alfa(p), beta(p)} este diferita de multimea / perechea neordonata {alfa(q), beta(q)}.

Demostratie

Daca pot distinge doua chei, inseamna ca am un reper care nu se schimba atunci cand rotesc sau intorc de nenumarate ori sirul. O informatie care nu se poate schimba este perechea neordonata {alfa(p), beta(p)}, dar ea este si suficienta deoarece este memoria maxima disponibila de informatii relevante a unei pozitii. In momentul cand mie mi se dau doua chei, le pot distinge daca si numai daca aceasta memorie a lor este identica.

O mica problema?

Atunci cand aflu, analizand sirul, despre doua chei de aceeasi forma ca le pot distinge, s-ar putea sa pot folosi acest fapt pentru a afla despre alte perechi de chei ca le pot distinge, desi inainte nu le puteam distinge. Asta s-ar putea sa se intample deoarece atunci cand verific egalitatea a doua siruri, a = a in mod normal. Dar daca eu am reusit sa disting intre cele 2 chei a, egalitatea dispare, s-ar putea spune ca a diferit de a, deoarece degeaba au aceeasi forma daca eu totusi le pot distinge.

Un rationament si complicatia dispare

Sa consideram cele doua chei pe care le-am distins prin faptul ca multimile mentionate mai sus sunt diferite. Ne punem intrebarea: pentru ce perechi de chei ar putea conta faptul ca ele sunt de fapt diferite? Pai pentru perechile de chei egal distantate de ele. Dar din moment ce le-am distins deja pe acestea doua chei, inseamna ca acele perechi de chei pentru care ar conta informatia, ele deja ar fi avut perechile (alfa, beta) diferite! Practic, informatia aceasta nu schimba cu nimic faptul ca doua chei ar putea sau nu sa fie acum distinse - daca se pot distinge, s-ar fi destins oricum.

Solutia

Trebuie doar sa afisam numarul de perechi de indici care au aceeasi pereche neordonata (alfa(p), beta(p)).

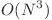- 22 de puncte

Se aleg doi indici p si q si se compara prin parcurgere liniara sirul alfa(p) cu beta(q), sirul alfa(p) cu alfa(q), etc. si se ia deiciza daca multumile sunt egale sau nu. Trebuie putina grija sa parcurgem circular sirul din input.

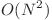- 51 de puncte

Egalitatea a doua siruri poate fi testata si altfel decat prin parcurgere directa. Sa ne uitam la un sir de caractere ca la un numar in baza 27, unde literele devin cifre - a devine 1, ..., z devine 26. Egalitatea a doua numere uriase se poate face cu probabilitate foarte mare daca le comparam resturile la impartirea cu doua numere, sa zicem prime, de ordinul zecilor sau sutelor de milioane. Daca vreti sa deveniti familiari cu aceasta tehnica numita hashing, puteti studia algoritmul Rabin-Karp.

Acum alfa si beta nu mai sunt siruri de caractere, ci niste numere mari pe care le retinem doar prin doua numere, resturile la impartirea cu doua numere de tip int alese dinainte. Acum, egalitatea poate fi verificata cu probabilitate foarte mare, in O(1).

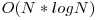- 100 de puncte

In loc sa luam toate perechile de indici (p, q) si sa verificam daca informatiile lor sunt egale, schimbam cumva tehnica numararii. Ne fixam informatia (perechea (alfa, beta)) si vedem cate perechi de indici au aceasta informatie. Practic, pentru fiecare pereche neordonata (alfa, beta) care apare macar o data intre cele N, notam cu F numarul de indici care au aceasta pereche. Atunci, trebuie doar sa adunam F * (F - 1) / 2 la raspuns, pentru ca atatea perechi ar fi spus ca sunt identice in solutia O(N^2).

Cum aflam F pentru fiecare pereche, fara sa parcurgem de fiecare data sirul de perechi? Mai intai, in cadrul fiecarei perechi, ordonam alfa <= beta conform unui comparator oarecare. Apoi sortam sirul de perechi, tot dupa un comparator oarecare. Astfel, perechile egale vor fi consecutive in sirul sortat. Acum, pentru fiecare segment maximal de perechi egale, F este egal cu marimea segmentului respectiv.

Solutia problemei ColorfulConflict

Solutia este prezentata de unul din concurenti,

Observatii:

1) Boundingbox-ul unei culori col este un drepunghi de coordinate (l1, c1, l2, c2), unde l1 este linia minima unde apare o celula de culoare col, c1 este coloana minima unde apare o celula de culoare col, iar l2 si c2 sunt definite analog numai ca sunt valorile maxime ale liniilor/coloanelor unde apare culoare col.

2) Daca exista 3 dreptunghiuri care nu se intersecteaza 2 cate 2 atunci va exista si o linie verticala sau orizontala care separa un dreptunghi de celelalte 2.

Idee generala

Pentru simplitate vom presupune ca linia de split este una orizontala(cazul vertical va fi tratat analog). Acum linia noastra de split ne-a impartit matricea in doua submatrici, sa le numim A si B. Este evident faptul ca A este un prefix al liniilor din matrice, iar B este un sufix al acestor linii. Tot ce trebuie sa verificam acum este ca in una din cele doua submatrici sa existe un dreptunghi complet inclus, iar in cealalta 2 dreptunghiuri complet incluse care nu se suprapun(este evident ca dreptunghiurile din submatricea A nu se vor suprapune cu cele din B).

Vom trata cazul in care vrem sa cautam 2 dreptunghiuri, care nu se intersecteaza, in A si unul singur in B (celalalt caz se trateaza asemanator).
Pentru a gasi un dreptunghi in B este suficient sa testam daca dreptunghiul care are linia de start maxima se afla sub linia de split.
Pentru a gasi 2 dreptunghiuri care nu se intersecteaza in A, ne vom folosi inca o data de observatia 2) si vom incerca sa gasim inca o linie de split intre dreptunghiurile respective.

Inca o observatie importanta este accea ca preferam sa coboram linia de split dintre A si B cat mai mult, pentru a oferi mai multa libertate in A, insa trebuie sa existe un dreptunghi complet inclus in B. De aici ne dam seama ca este optim sa fixam linia de split egala cu linia de start maxima($l1$) dintre toate dreptunghiurile.

Solutie finala

Pentru a stabili acum mai clar cum functioneaza algoritmul, putem observa ca in loc sa alegem linia de split mai intai pe verticala si dupa pe orizontala, este mult mai simplu sa rotim matricea cu 90^o, solutia fiind identica. Acum tot ce avem de facut este sa cautam dreptunghiul care are linia de start maxima, si sa testam daca deasupra acesteia exista 2 dreptunghiuri care sunt disjuncte. Acest ultim pas se trateaza similar: se va cauta o linie de split mai intai pe orizonatala si dupa pe verticala.

Daca in urma algortimului descris nu am gasit o solutie, inseamna ca aceasta nu exista.

Complexitate

Complexitatea finala este 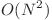si este optima, intrucat este aceeasi cu complexitatea de citire.

Solutia problemei Bazar

Ordinea in care sunt date punctele in input nu este tocmai relevanta, prin urmare le putem sorta crescator dupa coordonata x iar in caz de egalitate dupa y.

Un set de puncte unde sa punem zambilele este unul pe care taurii il pot parcurge mergand doar in Nord si Est este practic un subsir de indici S₁ < S₂ < ... < S_K pentru care y_Si ≤ y_Si+1 pentru orice i de la 1 la K-1. Asta deoarece coordonatele x sunt deja nedescrescatoare din sortare. Mai mult, aceasta este si ordinea in care cei doi tauri vor vizita zambielele. In plus, vom considera ca S₀ = 0 si x₀ = y₀ = 0.

Acum, mai trebuie sa remarcam faptul ca aria totala taiata de tauri pentru subsirul ales, este suma, pentru fiecare i de la 1 la K, din (x_Si - x_Si-1) * (y_Si - y_Si-1). Restrictia ca numarul de zambile sa fie maxim se traduce prin maximizarea lui K. Remarcam ca toate restrictiile si calculele au loc doar intre doua pozitii consecutive ale subsirului.

Aceste observatii ne conduc la urmatoarea idee: sa simulam cumva toate subsirurile, calculand, pentru fiecare punct i, 3 valori legate de subsirurile de lungime maxima nedescrescatoare dupa y care sa il aiba pe i ca ultim element in subsir.

• A_i = numarul maxim de puncte din vreun subsir pentru care i este ultimul punct (lungimea maxima)
• B_i = numarul de subsiruri de lungime maxima pentru care i este ultimul punct
• C_i = suma ariilor tuturor subsirurilor de lungime maxima pentru care i este ultimul din subsirurile considerate

Recurenta este urmatoarea: Pentru toti indicii 0 ≤ j < i pentru care y_j ≤ y_i, stim ca j poate fi penultimul element al subsirului pe care vrem sa il construim. Dintre toti acestia, ii vom considera doar pe aceia pentru care A_j este maxim, pentru a ne asigura ca subsirul are lungime maxima. Acum stim ca A_i = 1 + A_j, iar pentru a calcula B_i si C_i le vom initializa cu 0 si vom adauga, pentru fiecare j bun, valorile:

• B_i += B_j
• C_i += C_j + B_j * (x_i - x_j) * (y_i - y_i-1), deoarece dreptunghiul intre i si j apare in B_j subsiruri.

Pentru a afla raspunsul, nu trebuie decat sa adunam C_i, pentru toti indicii i pentru care A_i este maxim.

Putem initializa calculcul acestor valori in felul urmator:

• A₀ = 0
• B₀ = 1
• C₀ = 0

Pentru 23 de puncte, putem face calculul acesta parcurgand, pentru fiecare i toate pozitiile j mai mici si sa modificam valorile A_i, B_i, C_i conform recurentei. Complexitatea este O(N^2).

Pentru 44 de puncte, mai facem 2 observatii. Prima observatie este ca a afla A_i este acelasi lucru cu rezolvarea unei probleme clasice, subsirul de lungime maxima pentru sirul y_i. Putem rezolva aceasta parte a problemei cu solutia greedy pentru care e suficient sa stim sa cautam binar pentru a obtine complexitatea O(N * logN).

Acum, vom considera nivelul t ca fiind format din toti indicii i pentru care A_i = t. Fiecare nivel are proprietatea ca daca sortam punctele din el crescator dupa y, ele vor fi sortate descrescator dupa x. De ce aceasta? Pentru ca daca un punct are coordonatele x si y mai mari decat cele ale altui punt, ele vor face parte din niveluri diferite.

Prin urmare, dupa ce am calculat A_i, putem sorta din nou punctele crescator dupa A_i iar in caz de egalitate dupa y. Acum, fiecare nivel este un interval al acestui sir sortat. Acum, in schimb, indicii nu mai sunt sortati dupa x!

A doua observatie este ca atunci cand punctele sunt relativ uniform distribuite in plan, numarul de niveluri este O(sqrt(N)) iar pe fiecare nivel sunt O(sqrt(N)) puncte. Pentru a calcula valorile B_i si C_i, este suficient sa parcurgem intervalul corespunzator nivelului A_i si sa luam considerare acei indici j pentru care x_j ≤ x_i si y_j ≤ y_i. Astfel, obtinem complexitatea O(N * sqrt(N)) pe testele cu puncte random si O(N^2) in mod obisnuit.

Pentru 100 de puncte, mai facem doua observatii.

In primul rand, observam ca indicii j relevanti pentru calculul valorilor B si C ale unui indice i formeaza un interval compact dupa reordonarea facuta. Mai mult, atunci cand i creste, fie se schimba nivelul la care ne raportam, fie intervalul de indici j isi creste (poate deloc, dar oricum, niciodata nu isi scade) capetele stanag si dreapta. Asta pentru ca atunci cand il incremnetez pe i, y_i creste si el, prin urmare apar puncte noi j pentru care y_j ≤ y_i. In acelasi timp, incrementarea lui i il face pe x_i sa scada (deoarece, dupa, x, sunt sortati descrescator), prin urmare, anumitii indici j nu mai sunt buni de luat in calcul, pentru ca nu mai respecta conditia ca x_j sa fie mai mic sau egal cu x_i.

In al doilea rand, rescriem recurenta lui C_i in functie de B_j si C_j astfel incat sa putem adauga si scoate indicii j care devin valabili sau invalabili pentru o pozitie i, pentru momentul in care il schimbam pe i. Astfel,

• C_i += (C_j + B_j * x_j * y_j) - x_i * (B_j * y_j) - y_i * (B_j * x_j) + x_i * y_i * (B_j)

Este suficient sa mentinem patru variabile care tin suma fiecarei paranteze date de mai sus. Atunci cand adaugam sau scoatem un j din multimea indicilor valizi (care, cum spuneam, are forma de interval compact), e suficient sa modificam corespunzator sumele, care tin doar de j. Atunci cand vrem sa calculam C_i, doar folosim variabilele ca pe niste coeficienti pentru 1, x_i, y_i, respectiv x_i * y_i. Pentru a calcula B_i mai tinem o a cincea variabila care mentine doar suma din B_j.

In concluzie, cu mentiunea ca toate calculele trebuie facute in modulo 10^9 + 7, problema poate fi rezolvata in O(N * logN) cu cautare binara, sortare si plimbare liniara cu 2 pointeri. Timpii solutiei oficiale (in varianta ei neoptimizata) sunt de 4 ori mai mici decat limita de timp.