Solutii Algoritmiada 2013, Runda 3

Lista de probleme
3secv
Kgon
Move
Unicat
Paznici3
Flux2

3secv

Putem redefini subsecventa A1 ca si (1, P1 - 1) si A2 ca si (P1, P2). Notam M = max(A1, A2, A3), m = min(A1, A2, A3) si cu v[i] elementele sirului. Deci, trebuie sa gasim subsecventa din mijloc A2 (1 < P1 ≤ P2 < N) pentru care M - m este minima.

Daca am fixa P1 atunci am sti valoarea lui A1. Presupunem ca A1 va fi subsecventa cu valoarea minima. Rezulta ca m = A1. Trebuie sa plasam indicele P2 in intervalul [P1 + 1, N - 1] astfel incat M sa fie minim. Asta se intampla atunci cand P2 imparte intervalul in doua subsecvente cu sume cat mai apropiate. Rationamentul este similar pentru celelalte cazuri.

De aici ne vine ideea sa iteram cu P1 in intervalul [2, N - 1] si sa cautam binar cel mai mare indice P2 astfel incat $\sum\limits_{i=P1+1}^{P2}v[i] \leq \sum\limits_{j=P2+1}^{N}v[j]$ . Avandu-l si pe P2 fixat putem actualiza solutia. Incercam si solutia cu P2 + 1 (daca P2 + 1 < N) cand raportul sumelor se inverseaza si au valorile cele mai apropiate (pentru cazul >). 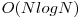Aceasta abordare are complexitatea $O(NlogN)$ si obtine 70 de puncte.

Putem reduce complexitatea la 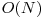$O(N)$ aplicand tehnica celor doi pointeri. Observam ca daca il incrementam pe P1, noul P2 va avea valoarea mai mare sau egala cu vechiul P2. Deci, pentru fiecare valoare a lui P1 il actualizam pe P2 mergand pas cu pas. P2 va avea nevoie de 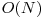$O(N)$ actualizari in total. Aceasta solutie obtine punctaj maxim.

Kgon

Pentru ca un subset de K puncte sa fie un poligon regulat, punctele subsetului trebuie sa fie echidistante. Aceasta distanta este 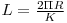$L = \frac{2\Pi R}{K}$ . Deci, pentru fiecare punct vom memora intr-un vector cnt cate puncte sunt in "spatele" lui astfel incat punctele consecutive (inclusiv cel curent) sunt la distanta L intre ele. Daca gasim un punct pentru care cnt[i] = K - 1, adaugam 1 la solutie deoarece avem certitudinea ca si distanta dintre ultimul punct si primul e aceeasi.

Deci, luam punctele in ordinea acelor ceasornicului (cea din datele de intrare) si cautam binar punctul p astfel incat D[p] - D[i] = L. Daca am gasit un astfel de punct, setam cnt[p] = cnt[i] + 1. Aceasta solutie are complexitatea 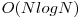$O(NlogN)$ si obtine 100 de puncte. Putem, insa, imbunatati solutia la 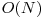$O(N)$ folosind tehnica celor doi pointeri (asemanator cu problema 3secv).

Move

Operatia pe care trebuie sa o folosim schimba doar ordinea relativa a elementelor. Deci, pentru a realiza un numar minim de operatii, trebuie sa gasim o submultime cat mai mare de elemente astfel incat elementele din submultime au ordinea relativa corecta, in cazul nostru sa fie sortate. Deci, trebuie sa gasim cel mai lung subsir crescator.

Ne ajuta faptul ca sirul este o permutare. Pentru fiecare interval vom memora indicele elementului in care se termina cel mai lung subsir crescator pentru acel interval. Parcurgem elementele in ordine crescatoare, deci in orice moment suntem siguri ca in arborele de intervale vor fi doar elemente cu valoare mai mica.

Daca lungimea celui mai lung subsir crescator este L atunci numarul minim de operatii este N - L. Parcurgem elementele in ordinea crescatoare a valorilor si pe fiecare element care nu face parte din cel mai lung subsir crescator il mutam inaintea celui de dinaintea sa (care e deja pe pozitia corecta). In general, mutam elementul cu valoarea x dupa elementul cu valoarea x - 1. A se observa ca relatia e valabila si pentru cazul in care il mutam pe 1 la inceputul permutarii.

Complexitatea este 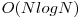$O(NlogN)$ .

Unicat

Pentru rezolvarea acestei probleme sunt necesare: algoritmul lui Manacher (problema PScPld) si hashuri.

Dupa rularea algoritmului lui Manacher pentru primul sir avem un vector P cu proprietatea ca P[i] = numarul maxim pentru care subsecventa (i - P[i], i + P[i]) este palindrom. Pentru fiecare pozitie i, luam toate palindroamele centrate in acea pozitie incepand cu cel mai mare si le introducem codul intr-un hash. Daca intalnim un palindrom deja introdus ne oprim, fiindca asta inseamna ca cele mai mici cu acelasi centru au fost introduse deja. Apoi, facem aceleasi operatii si pentru al doilea sir, cu diferenta ca atunci cand intalnim un palindrom care a fost introdus in primul hash, incrementam rezultatul.

Functia hash aleasa pentru codificarea subsecventelor poate sa varieze. Un exemplu este aici.

Complexitatea solutiei este 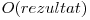$O(rezultat)$ , dar fiindca pentru un sir exista un numar liniar de palindroame distincte, ea este defapt $O(N)$ .

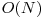Paznici3

Fiind vorba de un arbore (aciclic), putem folosi programarea dinamica. Starea este dp[i] = costul minim pentru a pazi tot subarborele cu radacina in i (si doar nodurile apartinand acestuia). Pentru a pazi nodul i, trebuie sa folosim un paznic j care are LCA (A[j], B[j]) = i. Costul in acest caz este egal cu costul paznicului j si costul de a pazi restul nodurilor nepazite de paznicul j. Pentru a afla al doilea cost, parcurgem lanturile A[j]-i si B[j]-i si insumam dp-urile nodurilor adiacente "laterale" care nu sunt pe lant. Pentru a calcula dp[i] luam minimul dintre toate cazurile (paznicii cu LCA in i). Aceasta metoda are complexitatea 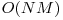$O(NM)$ deoarece parcurgem tot lantul pentru fiecare paznic.

Putem reduce complexitatea putem folosi doi arbori indexati binar. Vom face un DFS initial in care calculam pentru fiecare nod doua informatii: pInceput[i] in care memoram indexul de inceput pentru subarborele cu radacina in i si pSfarsit[i] indexul de sfarsit.

Pentru arborele

vectorii vor arata asa
pInceput = { 1, 2, 6, 3 }
pSfarsit = { 8, 5, 7, 4 }

Practic se rezerva un index si pentru sfarsitul de subarbore si vor fi in total 2N indecsi. In primul aib vom retine la indexul fiecarui nod valoarea dp[nod] iar in al doilea valoarea suma[nod] care semnifica suma dp-urilor fiilor lui nod. Pentru ca atunci cand facem query sa avem doar suma subarborelui care ne intereseaza, atunci cand facem update la un nod adaugam x la pozitia pInceput[nod] si -x la pozitia pSfarsit[nod]. Astfel raman doar sumele subarborilor "neinchisi" si restul se anuleaza.

Deci, pentru fiecare nod facem suma dp-urilor fiilor (acestea fiind calculate recursiv), calculam dp[nod] si actualizam cei doi aib. Cand calculam dp-ul nodului si luam fiecare paznic, putem face doua query-uri pentru fiecare ramura facand diferenta dintre suma sumelor si suma dp-urilor. Se reduc termenii care nu trebuie sa fie in suma si ramane exact suma dp-urilor care nu sunt pe lant. Observam ca facem update la aib-uri doar la sfarsitul recursivitatii si, deci, ele vor contine informatii doar despre nodurile de sub cel curent.

Acestea ne garanteaza complexitatea optima, insa mai putem optimiza solutia. Din moment ce oricum facem diferenta dintre cele doua informatii (suma si dp), putem sa folosim un singur aib care va retine suma[nod] - dp[nod] pentru fiecare nod. In acest caz, pe langa sumele returnate de query adaugam suma[nod]. Daca va ganditi la componenta sumelor, va dati seama de ce.

Bineinteles ca in loc de arbori indexati binar putem folosi si arbori de intervale.

Daca LCA-urile sunt implementate in 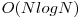$O(NlogN)$ iese complexitatea finala $O(NlogN + MlogN)$ .

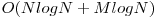Flux2

O rezolvare care calculeaza fluxul maxim de cost minim al grafului (folosind doar capacitatile si costul) si compara datele obtinute (fluxul si costul) cu datele curente grafului (care pot fi usor calculate) obtine 50 de puncte.

Exista doua cazuri in care planul angajatului nu e eficient: daca se poate mari fluxul sau daca se poate micsora costul. Pentru a verifica prima conditie, putem face un DFS din S. Daca, mergand doar pe muchii nesaturate (cu fluxul mai mic decat capacitatea), ajungem in D atunci fluxul poate fi marit cu cel putin o unitate. Pentru a verifica cea de a doua conditie, ne construim un nou graf G. Pentru fiecare muchie x->y de cost c din graful initial: daca e nesaturata, ducem o muchie x->y in G de cost c (deoarece mai putem inainta pe ea cu acest cost); daca are fluxul mai mare ca 0, ducem o muchie y->x in G de cost -c (deoarece exista posibilitatea de a reveni si sa alegem alt drum). Daca in noul graf G exista un ciclu de cost negativ, rezulta ca putem reduce costul din graful initial. Verificarea existentei ciclului de cost negativ se poate face cu algoritmul Bellman-Ford. Se va porni din nodul D, deoarece din acesta sigur exista drum catre potentialele cicluri de cost negativ (tot fluxul ajunge in D). Aceasta solutie obtine 100 de puncte.

infoarena informatica de performanta