| Fişierul intrare/ieşire: | lca.in, lca.out | Sursă | Arhiva educationala |
| Autor | Arhiva Educationala | Adăugată de | |
| Timp execuţie pe test | 1.4 sec | Limită de memorie | 131072 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Lowest Common Ancestor
Se dă un arbore cu rădăcină T. Cel mai apropiat strămoş comun a două noduri u şi v este nodul w care este strămoş al ambelor noduri u şi v şi are cea mai mare adâncime în T.
Considerăm că arborele T are n noduri şi are rădăcina în nodul 1. Dându-se o mulţime arbitrară P = {{u,v}}, cu m perechi neordonate de noduri din T, se cere să se determine cel mai apropiat strămoş al fiecărei perechi din P.
Date de intrare
Pe prima linie a fişierului de intrare lca.in se găsesc n şi m. Următoarea linie conţine n-1 numere naturale, cel de-al i-lea număr reprezentând tatăl nodului i+1 (nodul 1 fiind rădăcină nu are tată). Pe următoarele m linii se află câte o pereche de numere naturale, reprezentând elementele mulţimii P.
Date de ieşire
Fişierul de ieşire lca.out va conţine m linii, linia a i-a conţinând răspunsul celei de a i-a întrebări.
Restricţii
- 1 ≤ n ≤ 100 000
- 1 ≤ m ≤ 2 000 000
Exemplu
| lca.in | lca.out |
|---|---|
| 11 5 1 1 2 2 2 4 4 6 3 3 10 11 8 9 5 11 5 6 4 2 | 3 2 1 2 2 |
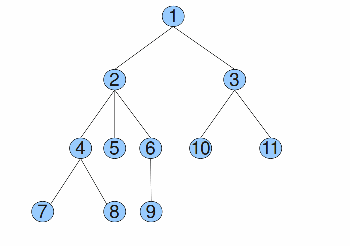
Explicaţie
Arborele din exemplu arată ca în figura alăturată...
Indicaţii de rezolvare
O primă soluţie, care caută LCA-ul celor două noduri mergând "în sus" pe ramurile nodurilor până când acestea se intersectează, având complexitatea de 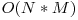 , ar trebui să obţină 30 puncte.
, ar trebui să obţină 30 puncte.
O altă soluţie descrisă în acest articol, având complexitatea finală de 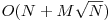 , ar trebui să obţină 60 puncte. Deşi nu este cea mai eficientă, avantajul acestei soluţii constă în faptul că se implementează foarte repede.
, ar trebui să obţină 60 puncte. Deşi nu este cea mai eficientă, avantajul acestei soluţii constă în faptul că se implementează foarte repede.
O altă soluţie relativ uşor şi rapid de implementat în condiţii de concurs este cea care foloseşte ideea de la problema Strămoşi. Se reţine pentru fiecare nod strămoşul cu 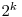 nivele mai sus, unde k ia valori între
nivele mai sus, unde k ia valori între  şi
şi 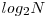 . Astfel, pentru fiecare query, se aduce nodul de pe nivelul mai mare pe acelaşi nivel cu celălalt în timp logaritmic, după care, tot în timp logaritmic, se poate afla LCA-ul celor două noduri. Complexitatea finală este deci
. Astfel, pentru fiecare query, se aduce nodul de pe nivelul mai mare pe acelaşi nivel cu celălalt în timp logaritmic, după care, tot în timp logaritmic, se poate afla LCA-ul celor două noduri. Complexitatea finală este deci 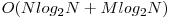 . Această soluţie ar trebui să obţină 70 puncte.
. Această soluţie ar trebui să obţină 70 puncte.
O soluţie ce se foloseşte de algoritmul lui Tarjan care rezolvă query-urile offline, bazându-se pe structura de date mulţimi disjuncte. Aceasta are complexitatea de 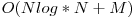 şi ar trebui să obţină 70 de puncte din cauza numărului mare de query-uri. Asemenea metodei cu RMQ prezentată mai jos, şi această metodă foloseşte o cantitate mai mare de memorie,
şi ar trebui să obţină 70 de puncte din cauza numărului mare de query-uri. Asemenea metodei cu RMQ prezentată mai jos, şi această metodă foloseşte o cantitate mai mare de memorie, 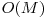 care în anumite condiţii nu se încadrează limitei de memorie. Un alt dezavantaj în anumite cazuri este faptul că query-urile nu se parcurg în ordine, ci se rezolvă offline, adică este necesară cunoaşterea lor în prealabil.
care în anumite condiţii nu se încadrează limitei de memorie. Un alt dezavantaj în anumite cazuri este faptul că query-urile nu se parcurg în ordine, ci se rezolvă offline, adică este necesară cunoaşterea lor în prealabil.
Soluţia care ar trebui să obţină 100 de puncte se bazează pe următoarea observaţie: „Cel mai apropiat strămoş comun a 2 noduri este nodul de nivel minim dintre primele apariţii ale nodurilor din query din reprezentarea Euler a arborelui.” În cazul de faţă, reprezentarea Euler a arborelui este următoarea, pe următorul rând găsindu-se nivelurile nodurilor:
| Reprezentarea Euler | 1 | 2 | 4 | 7 | 4 | 8 | 4 | 2 | 5 | 2 | 6 | 9 | 6 | 2 | 1 | 3 | 10 | 3 | 11 | 3 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nivelul | 0 | 1 | 2 | 3 | 2 | 3 | 2 | 1 | 2 | 1 | 2 | 3 | 2 | 1 | 0 | 1 | 2 | 1 | 2 | 1 | 0 |
Pentru exemplificare, nodurile 8 şi 9 au cel mai apropiat strămoş comun nodul cu nivel minim din secvenţa 8 4 2 5 2 6 9, adică nodul 2, care are nivelul 1. Pentru a implementa această soluţie, putem folosi arbori de intervale, având complexitatea 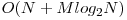 , soluţie care ar trebui să obţină 70 de puncte. Mai eficient, ţinând cont de restricţiile problemei, pentru determinarea minimului unei subsecvenţe se poate folosi RMQ. Astfel, complexitatea finală va fi
, soluţie care ar trebui să obţină 70 de puncte. Mai eficient, ţinând cont de restricţiile problemei, pentru determinarea minimului unei subsecvenţe se poate folosi RMQ. Astfel, complexitatea finală va fi 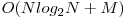 , această soluţie obţinând 100 de puncte. Dezavantajul acestei metode constă în faptul că se foloseşte
, această soluţie obţinând 100 de puncte. Dezavantajul acestei metode constă în faptul că se foloseşte 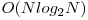 memorie, ceea ce poate fi un impediment în anumite cazuri.
memorie, ceea ce poate fi un impediment în anumite cazuri.
Un articol ce explică foarte bine atât RMQ, cât şi LCA se găseşte pe TopCoder.
Aplicaţii
- CT
- Atac
- Pirati
- Concurs
- Delay
- Radiatie
- Ratina
- Query on a tree I, spoj
- Query on a tree II, spoj
 Poti vedea testele pentru aceasta problema accesand
Poti vedea testele pentru aceasta problema accesand 