Solutii Infoarena Cup 2013
- Lista de probleme
- Secvbest
- RangeMode
- Bmat
- Nowhere-zero
Secvbest
Problema se rezolva cu ajutorul programarii dinamice. Incepem de la solutia evidenta, dupa care, cu ajutorul unor observatii, vom reduce complexitatea.
O prima rezolvare ar fi sa procesam matricea dp[i][j] = costul minim ca sa imparti primele j elemente din sir in i subsecvente. Recurenta arata cam asa: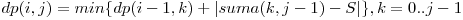 
, unde suma(a, b) = suma elementelor sirului intre indicii a si b (numerotati de la 0), inclusiv. Implementarea sumei se va face cu sume partiale. Momentan avem complexitatea 
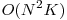ca timp si 
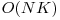ca si memorie. Putem retine doar ultimele doua linii ale dinamicii pentru a reduce memoria la 
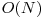. Solutia asta obtine 20 de puncte.
Presupunem ca pentru o anumita linie am calculat primele j-1 valori si acum avem de calculat dp[i][j]. Observam ca acea valoare absoluta din relatia de recurenta ne determina un indice p astfel incat suma(p, j-1) < S si p e minim. Practic imparte intervalul [0, j-1] in doua. Asta ne permite sa nu mai parcurgem indicii din stanga lui p, ci sa tinem pe parcurs indicele pentru care expresia dp(i-1,k) + sp(j-1) - sp(k-1) - S e minima (sp = suma partiala). In valoarea minimului retinem doar partea care e constanta: dp(i-1,k) - sp(k-1) - S. Pentru indicii din dreapta lui p ne trebuie minimul expresiei dp(i-1,k) + S - (sp(j-1) - sp(k-1)). Pentru acestea, folosim un deque si tinem minimul ca si in cazul anterior. Pentru a calcula dp[i][j] vom lua valoarea minima dintre cele doua minime. Deci, am redus complexitatea la 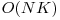ca si timp. Aceasta solutie obtine punctaj maxim.
