Algoritmi de baleiere (sweeping)
(Categoria Geometrie, Autor Stefan Istrate)
- Continut
- Introducere
- Prezentarea metodei
- Baleiere verticala
- Baleiere radiala
- Un alt algoritm pentru infasuratoarea convexa
- Aplicatii
- Bibliografie
Introducere
Sa presupunem ca vrem sa implementam un joc video in care personajul-jucator se poate plimba pe o harta planara cu obstacole (ziduri), iar in fiecare moment trebuie sa desenam pe ecran doar obstacolele pe care le vede acesta (chiar si partial). Mai precis, personajul reprezinta un punct, iar zidurile reprezinta segmente in plan. Ceea ce ne intereseaza sunt segmentele vizibile. Un punct este vizibil din alt punct daca segmentul ce le uneste nu intersecteaza niciun zid. Un zid este vizibil daca are cel putin un punct vizibil din pozitia jucatorului. Desigur, am putea alege cate 2 obstacole si trata toate cazurile care apar, dupa care sa pastram doar portiunile vizibile din cele 2 obstacole, dar aceasta abordare poate fi costisitoare uneori. Cel mai indicat ar fi sa gasim un mod eficient de "scanare" a planului prin care sa obtinem o lista de segmente vizibile.
Prezentarea metodei
Aceasta tehnica de "scanare" mentionata mai sus poarta numele de baleiere, sau sweeping (engl. sweeping = "maturare"). Exemplul de mai sus ilustreaza tocmai faptul ca tehnologiile si programele avansate din ziua de azi au la baza tehnici simple, dar nu lipsite de importanta. In majoritatea problemelor de geometrie vom intalni obiecte geometrice: puncte, drepte, segmente, figuri, corpuri. Avem nevoie sa stim sa le gestionam corect si sa extragem informatiile necesare in functie de situatia ivita.
Fie S o multime de obiecte in plan pentru care trebuie sa extragem anumite informatii si Q intrebarea la care trebuie sa raspundem. Abordarea intuitiva ar fi: alegem o dreapta (fie ea orizontala, verticala sau oblica) si o plimbam peste multimea de obiecte; in timpul baleierii ne asiguram ca sunt extrase toate informatiile referitoare la intrebarea Q; dupa ce am terminat scanarea, construim si afisam raspunsul pe baza informatiilor adunate. O descriere ceva mai explicita se poate vedea in imaginea de mai jos:
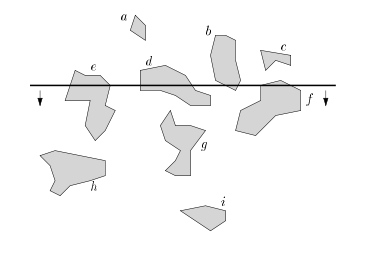
In timpul baleierii, la fiecare pas trebuie sa avem la dispozitie o structura de date continand toate obiectele intersectate de linia de baleiere. Pentru exemplul de mai sus, multimea de obiecte e traversata de sus in jos, iar la pasul curent sunt intersectate obiectele b, d, e, f. Continuand traversarea, vor urma, in ordine, eliminarea lui b din structura de date, eliminarea lui d, adaugarea lui g, etc. Dupa cum se observa, multimea obiectelor intersectate sufera destule modificari, ceea ce ne determina sa alegem o structura dinamica de date care sa ne confere eficienta. De cele mai multe ori, alegerea noastra va fi un arbore echilibrat. In cadrul algoritmului, vom vrea sa stim si care sunt momentele la care multimea obiectelor intersectate sufera modificari. Aceste momente vor reprezenta evenimentele, iar multimea acestora se va numi lista de evenimente. Iata pasii unui algoritm de baleiere (pastram notatia Q pentru intrebarea pe care o adresam):
Initializeaza lista de evenimente (L)
Initializeaza multimea obiectelor intersectate (M)
CAT TIMP L este nevida
Sterge din L evenimentul care urmeaza
DACA un nou obiect este intersectat de linia de baleiere
Adauga-l in M
DACA un obiect inceteaza a mai fi intersectat
Sterge-l din M
Aduna informatii privitoare la intrebarea Q
DACA este cazul
Adauga noi evenimente in L
Raspunde la intrebarea Q pe baza informatiilor adunateBaleiere verticala
Sa vedem acum o situatie mai concreta. Sa presupunem ca avem N dreptunghiuri in primul cadran al unui plan, cu laturile paralele cu axele de coordonate, iar latura de jos fixata pe axa OX. Cum am putea afla aria reuniunii tuturor dreptunghiurilor? De data aceasta, nici macar o solutie naiva nu este multumitoare. Cel mai simplu lucru la care ma gandesc ar fi calcularea ariei folosind principiul includerii si excluderii: se aduna ariile tuturor dreptunghiurilor, se scad ariile comune cator 2 dreptunghiuri, se aduna ariile comune cator 3 dreptunghiuri, etc. Este evident ca aceasta abordare este total nerecomandata din cauza timpului de rulare exponential. Ei bine, solutia la aceasta problema se bazeaza pe o baleiere verticala in care linia de baleiere este plimbata de la stanga la dreapta peste obiecte.
Sa observam mai intai ca laturile verticale ale dreptunghiurilor, precum si latura de jos pot fi ignorate, pastrand doar latura de sus pentru fiecare dreptunghi. Figura initiala este compusa din fasii verticale, fiecare fasie fiind delimitata in partea superioara de un segment (latura de sus a unui dreptunghi initial). Nu ne ramane de facut decat o parcurgere a fiecarei fasii si calcularea ariei acesteia, apoi insumarea tuturor.
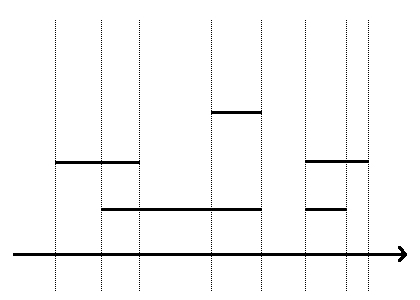
Sa analizam acum problema din perspectiva tehnicii pe care dorim sa o folosim. Evenimentele sunt, in acest caz, capetele stangi si cele drepte ale segmentelor orizontale. O alta observatie importanta este aceea ca, parcurgand o fasie cu linia de baleiere verticala, niciun segment nu este adaugat sau eliminat intre timp din multimea obiectelor intersectate. Schimbarile vor aparea doar la granita dintre fasii.
Inainte de a parcurge lista de evenimente, o vom sorta crescator in functie de abscisele capetelor segmentelor orizontale. Apoi, la fiecare pas, vom procesa toate evenimentele cu aceeasi abscisa. In ce consta acest lucru? Mai intai interogam structura de date continand obiectele deja intersectate si il alegem pe cel cu ordonata maxima Y. Aria ultimei fasii din stanga liniei de baleiere poate fi calculata usor cu formula Y * D, unde D este distanta pana la pozitia precedenta a liniei de baleiere, si apoi adaugata la aria totala. In cele din urma vom insera sau, dupa caz, vom sterge din structura de date obiectele a caror stare se schimba din cauza evenimentelor de la abscisa curenta. Asadar, vom avea nevoie de inserari, stergeri si interogari rapide. Putem alege un arbore de intervale (fiind necesara, inainte de toate, o normalizare a tuturor ordonatelor), un heap sau un arbore binar echilibrat de cautare in care ordonarea cheilor sa se faca dupa ordonata. Aveti, totusi, grija la duplicate: pot exista mai multe segmente orizontale cu aceeasi ordonata Y, ceea ce inseamna ca structura noastra de date trebuie sa gestioneze corect inserarea unui obiect cu o ordonata deja existenta sau stergerea acestuia.
Sa vedem acum analiza complexitatii. Avem nevoie de un timp O(N * log N) pentru sortarea listei de evenimente dupa abscisa, O(log N) (sau chiar O(1) la heap-uri si la set-urile din STL) pentru alegerea obiectului cu ordonata maxima, O(log N) pentru inserare si stergere in structura de date aleasa. Intrucat sunt 2 * N evenimente (cate 2 capete pentru fiecare segment), iar pentru fiecare efectuam o interogare si o adaugare / stergere, complexitatea finala va fi O(N * log N) + O(N) * (O(log N) + O(log N)) = O(N * log N).
Situatia se poate complica daca dreptunghiurile nu au o latura fixata pe axa OX. Nu mai este suficienta o simpla extragere a elementului maxim din structura de date, ci trebuie sa retinem mult mai multe informatii pentru a pastra complexitatea O(N * log N). Aceasta generalizare a fost data la Olimpiada Baltica de Informatica din 2001 (problema Mars Maps).
Baleiere radiala
Baleierea verticala nu este singura modalitate de scanare a planului. Pentru exemplificarea acestui lucru, se poate porni tot de la o situatie concreta: avand N puncte in plan, vrem sa aflam numarul maxim de puncte coliniare. O solutie triviala ar fi sa se fixeze 2 puncte si sa se numere toate punctele coliniare cu cele 2 dintre cele ramase. Complexitatea totala ar fi O(N3) care, in mod evident, nu este multumitoare. O imbunatatire semnificativa a algoritmului se obtine folosind tehnica de baleiere: se fixeaza un punct si se scaneaza planul cu ajutorul unei semidrepte avand originea in punctul fixat. Rotind semidreapta si suprapunand-o peste un punct, numaram daca mai exista si altele peste care s-a suprapus. Nu trebuie sa ne ingrijoreze faptul ca pot fi puncte coliniare cu unele gasite deja, dar care se afla in sensul opus celui dat de semidreapta aleasa, pentru ca oricum vom face o baleiere in fiecare punct si intr-unul din ele le vom numara corect in mod sigur pe cele coliniare. Implementarea eficienta a acestei metode presupune ca, odata fixata originea semidreptei, sa se sorteze toate celelalte puncte in functie de unghiul polar relativ la punctul fix. Complexitatea ajunge, astfel, la O(N2 * log N).
O aplicatie ceva mai spectaculoasa a baleierii radiale este gasirea unui triunghi dreptunghic cu varfurile printre N puncte date. Fixand un punct, putem cauta un triunghi dreptunghic care sa aiba unghiul drept in acel punct. Pentru acest lucru, vom sorta punctele exact ca la problema precedenta, dar baleierea o vom face rotind simultan 2 semidrepte cu originile in punctul fix, intre care mentinem in orice moment un unghi de 90 de grade. Cand ambele semidrepte se vor suprapune peste cate un punct, vom gasi ceea ce cautam. Complexitatea acestui algoritm va fi tot O(N2 * log N).
Un alt algoritm pentru infasuratoarea convexa
Aplicatii
Iata si o scurta lista de probleme care merita implementate:
- BOI 2001: Mars Maps
Bibliografie
Cosmin: Articolul asta despre baleiere http://www.topcoder.com/tc?module=Static&d1=tutorials&d2=lineSweep e destul de bine facut, poti sa trimiti lumea sa il citeasca. Chestia cu aria dreptunghiurilor nu e explicata si in articolul lui Mircea despre arbori de intervale? Mai bine ii trimiti acolo direct, decat sa le mai prezinti acelasi lucru inca o data. Si acolo parca complexitatea e O(n log n) in total.
Stefan: Articolul de pe Topcoder o sa-l mentionez impreuna cu altele la bibliografie. La complexitatea problemei cu aria dreptunghiurilor ai avut dreptate si este O(N * log N) (am modificat asta in articol). Cat despre articolul cu arbori de intervale (singurul astfel de articol in romana de care stiu este al doamnei Dana Lica, nu al lui Mircea), acolo este prezentata in detaliu aplicatia cu perimetrul reuniunii de dreptunghiuri, iar cea cu aria este trecuta doar la Probleme propuse. In plus, aplicatia pe care o prezint eu nu vrea sa reproduca pe niciuna din ele, ci este o varianta mult mai simplificata pentru a prezenta tehnica de baleiere. In problema pe care o prezint, un query sau un update vizeaza un singur element dintr-o multime, pe cand in problema generala a ariei dreptunghiurilor, update-ul vizeaza un interval de elemente.
Cosmin: :) da e al doamnei Lica .... perimetrul nu merge in O(n log n) perimetru e O(n log n + nr de segmente de pe perimetru) nu am citit articolul dar tind sa cred ca e prezentata treaba cu aria.
