Probleme de tăietură

Acest articol a fost adăugat de

Andrici Cezar •andrici_cezar
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena!

(Categoria Algoritmi, Autor Cosmin Negruşeri)

În cadrul acestui articol vom prezenta câteva enunţuri, împreună cu soluţiile corespunzătoare, reprezentative pentru clasa problemelor de tăietură.

Aplicaţia #1

Pentru un număr natural n dat, se cere numărul maxim de regiuni în care se poate împărţi planul folosind n drepte.

Rezolvare

Mai întâi vom prezenta două observaţii:

în configuraţia cu număr maxim de regiuni nu vom avea două drepte paralele, deoarece două drepte care se intersectează formează în plan patru regiuni, în timp ce două drepte paralele formează în plan doar trei regiuni;
pentru a obţine un număr maxim de regiuni nu vor exista trei drepte care să se intersecteze într-un punct deoarece astfel am „pierde” o regiune triunghiulară formată din punctele de intersecţie ale celor trei drepte.

Dacă aceste două condiţii sunt îndeplinite, vom vedea în continuare că orice configuraţie de n drepte împarte planul în acelaşi număr de regiuni. Notăm cu 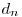$d_{n}$ acest număr.

Presupunem că valoarea 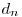$d_{n}$ este cunoscută; să vedem acum ce se întâmplă dacă mai adăugăm o dreaptă.

Această nouă dreaptă va fi intersectată de celelalte drepte în n puncte distincte. Fiecare segment de dreaptă şi semidreaptă în care este împărţită a (n + 1)-a dreaptă taie o regiune veche în două regiuni noi. De aici obţinem că 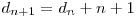$d_{n+1} = d_{n} + n + 1$ .

Aşadar, vom avea 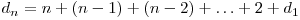$d_{n} = n + (n - 1) + (n - 2) + \ldots + 2 + d_{1}$ . Astfel, folosind identitatea 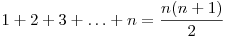$1 + 2 + 3 + \ldots + n = \dfrac{n(n+1)}{2}$ , obţinem $d_{n} = \dfrac{n(n + 1)}{2} + 1$ .

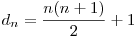Menţionăm că problemele în care se cere maximizarea numărului de regiuni în care un pătrat, un triunghi sau un cerc este împărţit de n drepte, au aceeaşi soluţie.

Aplicaţia #2

Dându-se un număr natural n, se cere numărul maxim de regiuni în care n cercuri pot împărţi planul.

Rezolvare

Este evident că oricare două cercuri trebuie să se intersecteze în exact două puncte, nu să fie tangente sau să nu se intersecteze deloc pentru că astfel am „pierde” o regiune, iar oricare trei cercuri nu au niciun punct comun.

Orice configuraţie care satisface această cerinţă va împărţi planul într-un număr maxim de regiuni. Vom nota cu 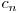$c_{n}$ numărul maxim de regiuni în care este împărţit planul de n cercuri.

Să vedem ce se întîmplă când adăugăm un nou cerc la această configuraţie. Cercul nou va fi intersectat de cele n cercuri în 2n puncte distincte, şi astfel va fi împărţit în 2n arce.

Fiecare dintre aceste arce împarte o zonă veche în două zone noi. De aici tragem concluzia că 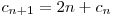$c_{n+1} = 2n + c_{n}$ .

Astfel, putem să scriem valoarea 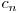$c_{n}$ ca $2(n-1) + 2(n-2) + \ldots + 2 + c_{1}$ .

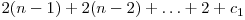De aici, folosind din nou identitatea $1 + 2 + \ldots + n = \dfrac{n(n+1)}{2}$ , avem că $c_{n} = n(n-1) + 2$ .

Este evident că şi problema în care se cere maximizarea numărului de regiuni în care este împărţită suprafaţa unei sfere de n cercuri are aceeaşi soluţie.

Aplicaţia #3: !! Really Strange !! (UVA)

Se dau n cercuri care se intersectează oricare două în două puncte şi nu există trei care se intersectează într-un punct; se cere să se determine numărul zonelor în care este împarţit planul de aceste n cercuri.
Restricţii: n ≤ 10¹⁰⁰.

Rezolvare

Observăm ca sunt indeplinite condiţiile de maximalitate cerute mai sus (vezi aplicaţia #2), deci rezultatul este 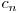$c_{n}$ . Singura problemă care rămâne este implementarea operaţiilor cu numere mari (dacă soluţia nu este implementată în Java).

Aplicaţia #4

Avem un număr natural n. Vrem să determinăm numărul maxim de regiuni în care n elipse pot împărţi planul.

Rezolvare

La fel ca şi în cazul cercurilor, nici aici nu trebuie să avem elipse tangente, elipse care să nu se intersecteze sau trei elipse care să se intersecteze într-un acelaşi punct. Elipsele trebuie să se intersecteze în patru puncte; dacă s-ar intersecta numai în două puncte, atunci configuraţia nu ar avea număr maxim de regiuni.

Notăm cu 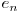$e_{n}$ numărul pe care îl căutăm. Câte regiuni noi apar cand adăugăm o nouă elipsă? O nouă elipsă va fi intersectată de fiecare dintre celelalte elipse în patru puncte, deci $e_{n+1} = 4n + e_{n}$ . De aici obţinem că $e_{n} = 2n(n-1) + 2$ .

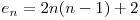Aplicaţia #5

Dându-se un număr natural n, se cere numărul maxim de regiuni în care n triunghiuri pot împărţi planul.

Rezolvare

Repetând raţionamentul de la problemele anterioare avem 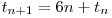$t_{n+1} = 6n + t_{n}$ , de unde $t_{n} = 3n(n-1) + 2$ .

Aplicaţia #6

Pentru n plane determinaţi numărul maxim de zone în care poate fi împărţit spaţiul folosind aceste plane.

Rezolvare

Şi în această problemă urmăm acelaşi raţionament. Este evident că trebuie ca fiecare plan să se intersecteze cu toate celelalte, că oricare trei plane trebuie să nu aibă nicio dreaptă comună, că oricare trei plane nu trebuie să fie paralele cu nicio dreaptă şi oricare patru plane nu trebuie să aibă niciun punct comun.

Notăm $p_{n}$ numărul maxim de zone în care n plane împart spaţiul. Dacă adăugăm un nou plan, acesta va fi intersectat de celelalte plane în n drepte, drepte printre care, datorită restricţiilor pe care le-am pus, nu vom avea două paralele sau trei care să se intersecteze într-un punct.

Acest plan va fi împărţit în 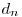$d_{n}$ regiuni de aceste drepte datorită restricţiilor impuse. Fiecare regiune din plan taie o zonă din spaţiu în două noi zone, de unde $p_{n+1} = d_{n} + p_{n}$ .

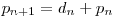Astfel avem:
$p_{n} = \dfrac{n(n-1)}{2} + 1 + \dfrac{(n-1)(n-2)}{2} + 1 + \ldots + \dfrac{2*1}{2} + 1 + p_{1}$
$p_{n} = \dfrac{n^2 - n + (n-1)^2 - (n-1) + \ldots + 2^2 - 2 + 1 - 1 + (n-1)}{2} + 2$
$p_{n} = \dfrac{ \dfrac{n(n+1)(2n+1)}{6} - \dfrac{n(n+1)}{2} + (n-1)}{2} + 2$
$p_{n} = \dfrac{ \dfrac{n^3}{3} + \dfrac{n^2}{2} + \dfrac{n}{6} - \dfrac{n^2}{2} - \dfrac{n}{2} }{2} + n + 1$
$p_{n} = \dfrac{n^3}{6} + \dfrac{5n}{6} + 1$ .

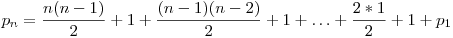
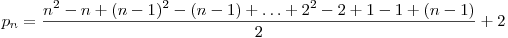
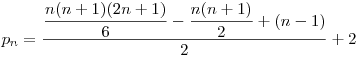
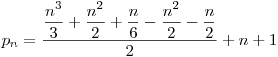
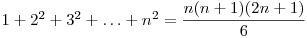Am folosit identităţile $1 + 2 + \ldots + n = \dfrac{n(n+1)}{2}$ şi $1 + 2^2 + 3^2 + \ldots + n^2 = \dfrac{n(n+1)(2n+1)}{6}$ , identităţi care se pot demonstra uşor prin inducţie.

Menţionăm că dacă vrem să împărţim un cub, un cilindru, o sferă etc. în număr maxim de regiuni folosind n plane, formula se păstrează.

Aplicaţia #7 (Bursele Agora, 2001)

Dându-se un număr natural n, să se determine numărul maxim de zone în care n sfere pot împărţi spaţiul.

Rezolvare

Pornim la fel ca în cazul problemei anterioare; oricare două sfere se vor intersecta şi nu vor exista trei sfere care să se intersecteze în acelaşi punct. Vom nota cu $s_{n}$ numărul maxim de regiuni în care poate fi împărţit spaţiul cu n sfere. Să vedem ce se întâmplă când adăugăm o sferă.

Această sferă va fi intersectată de toate celelalte n sfere în n cercuri; pentru ca numărul de regiuni noi să fie maxim aceste cercuri vor împărţi sfera într-un număr maxim de regiuni; acest număr este 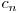$c_{n}$ aşa cum am discutat în aplicaţia #2.

Obţinem astfel:
$s_{n+1} = c_{n} + s_{n}$
$s_{n+1} = c_{n} + c_{n-1} + \ldots + c_{1}$
$s_{n+1} = n(n-1) + 2 + (n-1)(n-2) + 2 + \ldots + 2$
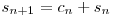
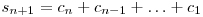
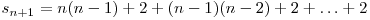
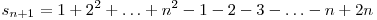$s_{n+1} = 1 + 2^2 + \ldots + n^2 - 1 - 2 - 3 - \ldots - n + 2n$ , de unde $s_{n} = \dfrac{n(n^2 - 3n + 8)}{3}$ .

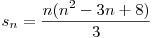Aplicaţia #8: Thinking Backward (UVA)

Se consideră un număr N care reprezintă numărul maxim de regiuni în care poate fi împărţit planul de către m elipse, n cercuri şi p triunghiuri. Se cere să se determine toate valorile posibile pentru m, n şi p.
Restricţii: N întreg, fără semn, reprezentabil pe 32 biţi; 0 ≤ m < 100; 0 ≤ n < 20 000; 0 ≤ p < 100.

Rezolvare

Dacă am cunoaşte pentru trei parametri m, n şi p care este numărul maxim de părţi în care poate fi împărţit planul de către m elipse, n cercuri şi p triunghiuri, atunci am putea încerca toate posibilităţile pentru m, n şi p şi am găsi şi tripletele pentru care rezultatul ar fi egal cu N.

Am putea optimiza puţin acest algoritm iterând doar pe toate valorile m şi p; astfel vom obţine o ecuaţie cu necunoscuta n şi vom efectua 10 000 de rezolvări de ecuaţii în loc de 200 000 000 de comparaţii.

Să vedem cum găsim numărul maxim de zone. Din nou, oricare două figuri se intersectează în număr maxim de intersecţii, un cerc cu o elipsă în patru puncte, un cerc sau o elipsă cu un triunghi în şase puncte.

Mai întâi punem cele m elipse în plan; ele vor împărţi planul în 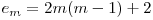$e_{m} = 2m(m-1) + 2$ regiuni.

În continuare adăugăm cercurile. Să notăm numărul maxim de zone în care n cercuri şi m elipse pot împărţi planul prin 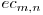$ec_{m ,n}$ . Dacă valoarea 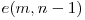$e(m,n-1)$ este cunoscută, atunci, în momentul în care adăugăm un nou cerc, acesta va fi intersectat de m elipse în 4m puncte şi de n-1 cercuri în 2(n-1) puncte, deci cercul va fi împărţit în 4m + 2(n-1) arce care vor împărţi tot atâtea regiuni care existau deja în câte două regiuni noi.

Aşadar, avem:
$ec_{m,n} = 4m + 2(n-1) + ec_{m,n-1}$
$ec_{m,n} = 4m + 2(n-1) + 4m + 2(n-2) + \ldots + 4m + 2 + ec_{m,0}$
$ec_{m,n} = 4m(n-1) + n (n-1) + 2m(m-1) + 2$ .

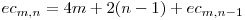
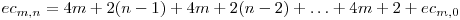
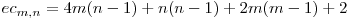Să vedem ce se întâmplă când adăugăm triunghiurile. Vom nota prin $ect_{m, n, p}$ numărul maxim de zone în care poate fi împărţit planul de m elipse, n cercuri şi p triunghiuri.

Dacă valoarea 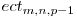$ect_{m, n, p - 1}$ este cunoscută, atunci, în momentul în care vom adăuga un nou triunghi acesta va intersecta cele m cercuri în 6m puncte, cele n elipse în 6n puncte şi cele p-1 triunghiuri în 6(p-1) puncte, formându-se 6m + 6n + 6(p-1) noi zone.

Aşadar, obţinem:
$ect_{m, n, p} = 6(m + n + p - 1) + ect_{m, n, p - 1}$
$ect_{m, n, p} = 6(m + n + p - 1 + m + n + p - 2 + \ldots + m + n + 1) + ect_{n, m, 0}$
$ect_{m, n, p} = 6(p-1)(m+n) + 3p(p-1) + 4m(n-1) + n(n-1) + 2m(m-1) + 2$ .

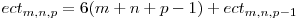
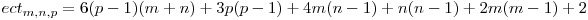Problemele anterioare au fost cam matematice şi ele sunt numite de obicei de olimpici peiorativ ca „probleme de formulă”. Majoritatea olimpicilor la informatică participă aici pentru că matematica nu le „place atât de mult” şi, deci, nici apariţia unor probleme ca cele de mai sus care sunt „mai mult de mate decât de info” nu îi prea încântă.

Cum poate fi rezolvată o problemă de formulă fără să avem intuiţia matematică sau cunoţinţele matematice necesare?

Uneori elevii apelează la următorul truc: determină primele câteva valori manual sau cu ajutorul unor algoritmi brute force şi apoi speră ca formula să fie de o anumită formă; de exemplu ar putea fi un polinom de un grad mic. De exemplu, am putea presupune că formula este de forma 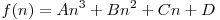$f(n) = An^3 + Bn^2 + Cn + D$ . Calculând primele patru valori, vom cunoaşte valorile f(1), f(2), f(3), f(4). Atribuind pe rând lui n valorile 1, 2, 3 şi 4 putem obţine un sistem de ecuaţii cu necunoscutele A, B, C şi D.

O altă posibilitate este să încercăm să vedem cum se comportă şirul de numere: are o creştere polinomială sau exponenţială, apar valorile lui în triunghiul lui Pascal etc. Dacă aveţi la dispoziţie o conexiune la internet (participaţi la un concurs online sau vă antrenaţi), puteţi căuta valorile din şirul de soluţii la Eciclopedia Online a şirurilor de întregi care este o resursă foarte utilă în cazul problemelor de acest gen.

Aplicaţia #9: Internet Problem Solving Contest, 2000

Se consideră n drepte în plan, fiecare dreaptă este descrisă prin două puncte distincte aflate pe acea dreaptă. Se cere să se determine pentru această configuraţie în câte zone este împărţit planul.
Restricţii: n ≤ 1000.

Rezolvare

În sfârşit o problemă în care avem nevoie să folosim calculatorul şi talentul de programator... Vom folosi aceeaşi idee ca şi în cazul celorlalte probleme, adică numărăm pe rând în câte zone este împărţit planul de prima dreaptă, primele două drepte până ajungem la toate cele n drepte. Aşadar, vom adăuga în ordine dreptele la configuraţia noastră.

Când adăugăm o dreaptă, aceasta va fi intersectată de dreptele deja adăugate în k puncte nu neapărat distincte; pe noi ne intereseaza punctele distincte şi, pentru a le număra, putem sorta punctele (în complexitate O(k log k)) sau putem folosi o tabelă de dispersie, caz în care timpul necesar devine O(k).

Dacă numărul de puncte distincte este egal cu m, atunci numărul total de zone va creşte cu m.

Astfel, algoritmul are complexitatea O(n² log n) dacă folosim sortarea sau O(n²) dacă folosim tabela de dispersie.

Aplicaţia #10: The partition of a cake (UVA)

Avem un tort în formă pătratică; dimensiunea acestuia este 1000 × 1000. Folosim un cuţit pentru a tăia tortul. Va trebui să determinăm în câte bucăţi a fost împărţit tortul după o serie de tăieturi. Numărul tăieturilor nu va fi mai mare de 8. După tăiere, lungimea oricărei laturi a partiţiei nu va fi mai mică decât unu. Coordonatele vârfurilor tortului vor fi (0,0) (0,1000) (1000,1000) (1000,0). Tăieturile se vor intersecta în două puncte cu marginile tortului. În imagine este prezentat un tort tăiat în zece bucăţi.

Rezolvare

Soluţia este asemănătoare celei pentru problema anterioară. Dimensiunile datelor de intrare sunt foarte mici pentru problema aceasta; este posibil ca autorii să fi vrut ca problema să fie rezolvabilă şi folosind împărţiri efective în poligoane a pătratului.

Aplicaţia #11: Count the faces (UVA):

Se dă un graf planar descris prin noduri şi muchii (un graf este planar dacă există o modalitate de a-l desena în plan fără ca muchiile să se intersecteze decât în noduri). Se cere să se determine în câte regiuni împarte planul graful dat. În imagine este prezentat un graf în care feţele sunt numerotate.

Rezolvare

Este interesant faptul că în această problemă nu este dată configuraţia în plan a grafului, ci doar structura lui. Un graf poate fi reprezentat în mai multe moduri în plan, ceea ce ne poate face să credem că ar exista o formulă pentru rezolvarea problemei.

Există într-adevăr o astfel de formulă care poartă denumirea de formula lui Euler pentru grafurile planare. Dacă graful este conex, această formulă este f - m + n = 2, unde prin f am notat numărul de feţe, prin m numărul de muchii şi prin n numărul de vârfuri. Formula include faţa exterioară. Această formulă poate fi demonstrată în foarte multe moduri. Dacă doriţi să vedeţi 19 metode de demonstrare puteţi să vizitaţi Nouăsprezece demonstraţii ale formulei lui Euler: V-E+F=2.

O demonstraţie simplă se bazează metoda inducţie matematice pornind de la un arbore şi adăugând pe rând câte o muchie. La început avem o singură faţă, cea infinită, deci ipoteza de inducţie se verifică: 1 - (n - 1) + n = 2. Fiecare muchie adăugată împarte o faţă în două, deci, dacă inainte aveam f - m + n = 2, acum vom avea f₁ - m₁ + n = 2, unde f₁ = f + 1 şi m₁ = m + 1. Aşadar, am demonstrat formula şi putem foarte uşor să rezolvăm problema. Mai trebuie numai să avem grijă ca pentru fiecare componentă conexă să numărăm faţa infinită. Această formulă este adevarată şi în spaţiu pentru poliedre.

Aplicaţia 12: Cercuri (Algoritmus)

Se consideră n cercuri în plan. Se cere să se determine numărul zonelor finite în care cercurile date împart planul. Cercurile sunt date prin coordonatele centrului şi rază. În figură este prezentat un exemplu. Numărul căutat al zonelor este 11.

Rezolvare

Problema nu poate fi rezolvată folosind aceleaşi idei deoarece aici apar cazuri speciale, cum ar fi punctele de tangenţă, faptul că nu toate cercurile trebuie să se intersecteze între ele (ceea ce duce la apariţia unor zone ca rezultat al unui ciclu de cercuri, aceste zone neputând fi numărate prin procedeul folosit).

O altă idee ar fi folosirea geometriei computaţionale, dar aceasta pare destul de anevoioasă; lucrurile se simplifică mult dacă abordăm problema prin prisma unor noţiuni de teoria grafurilor.

Fiecare punct de intersecţie va fi considerat un nod. Două noduri vor fi legate printr-o muchie dacă există un cerc pe care să se afle amândouă, iar între ele să nu existe niciun alt punct de intersecţie. Acum vom folosi identitatea lui Euler, prezentată în cadrul soluţiei problemei anterioare.

Pentru această problemă nu trebuie să numărăm şi faţa exterioară, deci formula folosită va fi F = M - V + 1. Această formulă este adevărată doar în cazul unei singure componente conexe. Pentru mai multe componente, formula devine F = M - V + C, unde C este numărul de componente conexe.

O atenţie deosebită trebuie acordată punctelor de intersecţie prin care trec mai mult de două cercuri, pentru a nu le număra de mai multe ori. Putem rezolva această problemă prin sortarea punctelor de intersecţie ale unui cerc cu toate celelalte cercuri.

De asemenea, este necesară eliminarea cercurilor identice (cu acelaşi centru şi raze egale). Din orice mulţime formată din astfel de cercuri este păstrat doar un singur element.

Deoarece pentru fiecare cerc este necesară o sortare a punctelor de intersecţie, complexitatea algoritmului va fi O(n² log n).

Bibliografie

A.M. Iaglom, I. M. Iaglom, Probleme neelementare tratate elementar, Editura Tehnică, Bucureşti, 1962;
I. Tomescu, Probleme de combinatorică şi teoria grafurilor, Editura Didactică şi Pedagogică. Bucureşti, 1981;
Colecţia GInfo;

remote content

infoarena informatica de performanta

Probleme de tăietură

Aplicaţia #1

Rezolvare

Aplicaţia #2

Rezolvare

Aplicaţia #3: !! Really Strange !! (UVA)

Rezolvare

Aplicaţia #4

Rezolvare

Aplicaţia #5

Rezolvare

Aplicaţia #6

Rezolvare

Aplicaţia #7 (Bursele Agora, 2001)

Rezolvare

Aplicaţia #8: Thinking Backward (UVA)

Rezolvare

Aplicaţia #9: Internet Problem Solving Contest, 2000

Rezolvare

Aplicaţia #10: The partition of a cake (UVA)

Rezolvare

Aplicaţia #11: Count the faces (UVA):

Rezolvare

Aplicaţia 12: Cercuri (Algoritmus)

Rezolvare

Bibliografie