Revizia anterioară Revizia următoare
Probleme cu secvenţe
(Categoria Diverse, autor Cosmin Negruşeri)
- Cuprins
- Introducere
- Problema 1 ( Subsecvenţa de sumă maximă )
- Problema 2 ( Maximum Sum )
- Problema 3 ( SequenceQuery )
- Problema 4
- Problema 5
- Problema 6 ( Secvenţă )
- Problema 7 ( Agricultura )
- Problema 8 ( Secvenţa 2 )
- Problema 9 ( Sum )
- Problema 10 ( Secvenţa 3 )
- Problema 11 ( XorMax )
Introducere
Acest articol prezintă o serie de probleme înrudite cu problema subsecvenţei de sumă maximă, însoţite de rezolvări eficiente. Problemele prezentate pot apărea oricând ca subprobleme în concursurile de programare, studierea lor mărind în mod util bagajul de cunoştinţe al unui elev pasionat de algoritmică.
Problema 1 ( Subsecvenţa de sumă maximă )
Se dă un şir de N numere întregi (a1, a2, ..., aN). Să se determine o subsecvenţă (ai, ai+1, ..., aj) care să aibă suma maximă.
Exemplu
Pentru secvenţa de numere (-1, 2, 3, -4, -2, 2, 1, -3, -2, -3, -4, 9, -2, 1, 7, 8, -19, -7, 2, 4, 3), o subsecvenţă de sumă maximă este (9, -2, 1, 7, 8).
Rezolvare
Prima rezolvare care ne vine în minte are complexitatea O(N3) şi constă în determinarea sumei fiecărei subsecvenţe posibile şi reţinerea maximului acestor sume. Este evident că anumite sume parţiale sunt calculate de mai multe ori.
Putem reduce complexitatea la O(N2) ţinând cont de faptul că suma subsecvenţei a[i..j] este egală cu suma subsecvenţei a[i..j-1], la care se adună a[j]. Păstrăm într-un şir sum[i] - suma elementelor din subsecvenţa a[1..i]. Pentru a determina suma elementelor din subsecvenţa a[i..j] facem diferenţa sum[i] - sum[j-1].
Ideea poate fi rafinată calculând pentru fiecare indice i numărul best[i], reprezentând subsecvenţa de sumă maximă cu capătul drept în i. Este uşor de observat că best[i] = max(sum[i] - sum[j-1]), unde j ia valori de la 1 la i. Relaţia anterioară se mai poate scrie best[i] = sum[i] - min(sum[j-1 ]). Obţinem astfel un algoritm liniar care ne determină subsecvenţa de sumă maximă cerută.
sum[0] = 0;
for (i = 1; i <= N; i++) sum[i] = a[i] + sum[i-1];
min = sum[0];
bestSum = -INFINIT;
for (i = 1; i <= N; i++) {
best[i] = sum[i] - min;
if (min > sum[i]) min = sum[i];
if (bestSum < best[i]) bestSum = best[i];
}O altă metodă de calcul poate fi dedusă folosind paradigma Divide Et Impera. La fiecare pas împărţim şirul în jumătate şi aflăm subsecvenţele de sumă maximă din cele două jumătăţi. După aceea trebuie să găsim subsecvenţa de sumă maximă ce are un capăt în fiecare din cele două jumătăţi ale sirului. Pentru aceasta alipim sufixul de sumă maximă a primei jumătăţi cu prefixul de sumă maximă a celei de-a doua.
int getMaxSubsequence(int l, int r) {
if (l == r) return a[l];
mid = (l + r) / 2;
bestL = getMaxSubsequence(l, mid);
bestR = getMaxSubsequence(mid + 1, r);
suf = 0;
pre = 0;
maxSuf = -INFINIT;
maxPre = -INFINIT;
for (i = mid; i >= l; i--) {
suf += a[i];
if (maxSuf < suf) maxSuf = suf;
}
for (i = mid + 1; i <= r; i++) {
pre += a[i];
if (maxPre < pre) maxPre = pre;
}
return max(bestL, max(bestR, maxPre + maxSuf));
}O idee bazată pe paradigma programării dinamice ar fi să folosim un şir best[ i ], reprezentând suma maximă a unei subsecvenţe ce se termină în a[i]. Problema se rezolvă cu următoarea formulă de recurenţă: best[i] = max(a[i], best[i-1] + a[i]). Formula poate fi demonstrată prin inducţie matematică.
O ultimă idee ar fi să partiţionăm şirul în subsecvenţe încât fiecare să aibă ambele capete cât mai mici posibile şi suma elementelor subsecvenţei să fie negativă. Pentru exemplul dat avem următoarea partiţionare [-1], [2, 3, -4, -2], [2, 1, -3, -2], [-3], [-4], [9, -2, 1, 7, 8, -19, -7], [2, 4, 3]. O subsecvenţă de sumă maximă va avea primul capăt la începutul unei astfel de subsecvenţe, acest lucru explicându-se prin faptul că în caz contrar secvenţa poate fi mărită în stânga (orice secvenţă din cele alese pentru partiţionare are toate prefixele de sumă pozitivă, în afară de prefixul ce reprezintă întreaga subsecvenţă). De asemenea, orice subsecvenţă de sumă maximă nu va conţine elemente din altă parte a partiţiei, pentru că dacă subsecvenţa se întinde pe mai multe părţi, atunci putem elimina prefixul subsecvenţei care reprezintă o parte a partiţiei, acea parte având suma negativă.
sum = -INFINIT;
bestSum = -INFINIT;
for (i = 1; i <= N; i++) {
sum += a[i];
if (sum < 0) {
sum = 0;
continue;
} else
if (sum >= bestSum) bestSum = sum;
}Problema 2 ( Maximum Sum )
Se dă o matrice de dimensiuni NxN cu elemente întregi. Se cere determinarea unei submatrici a cărei elemente au suma maximă.
Exemplu
Pentru matricea![\[ \left( \begin{array}{cccc}0 & -2 & -7 & 0 \9 & 2 & -6 & 2 \-4 & 1 & -4 & 1 \-1 & 8 & 0 & -2 \end{array} \right)\] \[ \left( \begin{array}{cccc}0 & -2 & -7 & 0 \9 & 2 & -6 & 2 \-4 & 1 & -4 & 1 \-1 & 8 & 0 & -2 \end{array} \right)\]](http://www.infoarena.ro/static/images/latex/4803085c25ba4c147f20981b47e7b734_22.50023pt.gif) submatricea de sumă maximă este următoarea:
submatricea de sumă maximă este următoarea:![\[ \left( \begin{array}{cc}9 & 2 \-4 & 1 \-1 & 8 \end{array} \right)\] \[ \left( \begin{array}{cc}9 & 2 \-4 & 1 \-1 & 8 \end{array} \right)\]](http://www.infoarena.ro/static/images/latex/c9c94ab8a91b4daa70fdabcf22db7651_16.50017pt.gif)
Rezolvare
Putem folosi trucul construirii sumelor parţiale din rezolvarea anterioară, pentru cazul 2D. Păstrăm în sum[i][j] suma tuturor elementelor a[i1][j1] cu proprietatea că 1 <= i1 <= i, şi 1 <= j1 <= j. Putem calcula sumele prin metoda programării dinamice (complexitate O(N2)) folosind formula sum[i][j] = a[i][j] + sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1]. Acum pentru a calcula suma elementelor din matricea cu colţurile (i1, j1) şi (i2, j2), unde i1 <= i2 şi j1 <= j2, este suficient să facem calculul sum[i2][j2] - sum[i1-1][j2] - sum[i2][j1-1] + sum[i1-1][j1-1]. Astfel putem evalua suma din fiecare submatrice în timp constant, deci rezolvarea are ordinul de complexitate O(N4).
O altă idee ar fi ca pentru fiecare pereche (i1, i2) fixată să determinăm perechea optimă (j1, j2). Dacă avem liniile i1 şi i2 fixate atunci problema se transformă din una bidimensională în una unidimensională. Astfel pentru fiecare coloană j vom considera b[j] ca sumă a elementelor a[i][j] cu proprietatea că i1 <= i <= i2. În exemplul nostru, dacă i1 = 2 şi i2 = 3, atunci avem b1 = 9 + (-4), b2 = 2 + 1, b3 = (-6) + (-4) şi b4 = 2 + 1. Pentru a rezolva problema unidimensională folosim unul din algoritmii liniari prezentaţi mai sus, astfel obţinându-se un algoritm de complexitate totală O(N3). Acest truc de a fixa două linii pentru a transforma problema în una unidimensională este util în multe probleme pe matrice sau cu puncte în plan.
Cel mai bun algoritm cunoscut pentru această problemă are complexitatea 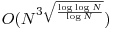 [3] şi este mai mult un algoritm teoretic decât unul practic, uşor implementabil.
[3] şi este mai mult un algoritm teoretic decât unul practic, uşor implementabil.
Problema 3 (SequenceQuery - Bursele Agora 2005/2006 Runda 1)
Se consideră un şir A = (a1, a2, ..., aN), format din numere întregi (-100.000 <= ai <= 100.000), şi M perechi de numere (x, y) (1 <= N, M <= 100.000). Pentru fiecare pereche ordonată de indici (x, y) trebuie determinată subsecvenţa de sumă maximă a subşirului ax, ax+1, ..., ay. Subsecvenţele alese trebuie să conţină cel puţin un element.
Exemplu
Pentru şirul (-1, 2, 3, -2, 4, -3, 8, -3, 1) şi intervalele [1, 5], [4, 8] si [6, 6] avem soluţiile:
- 7 pentru subsecvenţa (-1, 2, 3, -2, 4);
- 9 pentru subsecvenţa (-2, 4, -3, 8, -3);
- -3 pentru subsecvenţa (-3).
Rezolvare
Putem obţine un algoritm de complexitate O(MN) folosind algoritmii liniari din prima problemă, dar să vedem cum putem reduce complexitatea folosind alte abordări. Mai întâi calculăm şirul sum al sumelor parţiale, după care împărţim şirul în k subsecvenţe de lungimi egale [n/k], şi păstrăm următoarele informaţii pentru fiecare din ele:
- max[i] - cea mai mare valoare sum[j], unde n/k * (i-1) < j <= n/k * i;
- min[i] - cel mai mic sum[j-1], unde n/k * (i-1) < j <= n/k * i;
- best[i] - valoarea subsecventei de suma maxima a secventei curente.
Acum, pentru a afla subsecvenţa de sumă maximă a subsecvenţei a[x..y] studiem cele două cazuri posibile:
1. Dacă elementele de indice x şi y aparţin aceleiaşi subsecvenţe, atunci putem găsi ceea ce căutăm folosind algoritmul liniar direct pe şirul a[x..y] (complexitate O(n/k)).
2. Dacă nu sunt în aceeaşi secvenţă, atunci vom împărţi şirul a[x..y] în:
- un prefix de subsecvenţă din cele ce aparţin partiţionării,
- un sufix de subsecvenţă,
- zero sau mai multe subsecvenţe complete ce aparţin partiţionării,
după care rezolvăm problema pentru sufix şi prefix prin metoda liniară ( O(n/k) ), şi determinăm în O(1) pentru fiecare bucată în care este spart şirul a[x..y] subsecvenţa ei de sumă maximă.
Mai rămâne să găsim subsecvenţa de sumă maximă cu capătul în bucăţi diferite. Pentru două bucăţi fixate i <= j, subsecvenţa de sumă maximă ce are câte un capăt în fiecare bucatăm are valoarea max[j] - min[i]. Determinarea subsecvenţei de sumă maximă cu capetele în bucăţi diferite devine astfel de complexitate O(k). Deci pentru a rezolva o întrebare trebuie să facem O(n/k + k) calcule. Pentru a reduce complexitatea problemei considerăm pe k = sqrt(n). Complexitatea totală a acestei soluţii este O(N + M sqrt(N)).
Să vedem ce se întâmplă pe exemplu:
| a | - | -1 | 2 | 3 | -2 | 4 | -3 | 8 | -3 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| sum | 0 | -1 | 1 | 4 | 2 | 6 | 3 | 11 | 8 | 9 |
Şirul e împărţit în trei subsecvenţe [-1, 2, 3], [-2, 4, -3], [8, -3, 1]:
| max | 4 | 6 | 11 |
|---|---|---|---|
| min | -1 | 2 | 8 |
| best | 5 | 4 | 8 |
Pentru a răspunde la întrebarea [1, 5] trebuie să răspundem la cele două subsecvenţe componente [1..3] şi [4..5]. Soluţia optimă pentru [1..3] este best1 = 5. Soluţia optimă pentru [4..5] o determinăm folosind algoritmul liniar, ea fiind 4. Acum, pentru a determina subsecvenţa de sumă maximă cu câte un capăt în fiecare interval folosim formula max(sum[i]) - min(sum[j-1]), unde 4 <= i <= 5 şi 1 <= j <= 3. Valoarea max(sum[i]) o găsim parcurgând intervalul [4, 5] ca fiind 6, iar valoarea min(sum[j-1]) o avem deja calculată în min1. De aici obţinem rezultatul 7.
O soluţie similară poate fi obţinută cu ajutorul arborilor de intervale. Mai întâi creăm arborele de intervale. Pentru fiecare interval aflăm elementele min, max şi best astfel:
- min[x..y] = minim(min[x..(x+y)/2], min[(x+y)/2 + 1 .. y]);
- max[x..y] = maxim(max[x..(x+y)/2], max[(x+y)/2 + 1 .. y]);
- best[x..y] = maxim(best[x..(x+y)/2], maxim(best[(x+y)/2 + 1 .. y], max[(x+y)/2 + 1 .. y] - min[x..(x+y)/2])).
Acum pentru a răspunde la întrebările din problemă fiecare interval va fi împărţit în O(log N) subintervale canonice care apar în arborele de intervale. Apoi printr-o parcurgere asemănătoare celei din rezolvarea anterioară se poate obţine rezultatul pentru fiecare întrebare în O(log N). Soluţia va avea complexitatea O(N + M log N).
În următorul desen observăm structura unui arbore de intervale pentru un şir cu 16 elemente. Daca se pune întrebarea [2, 11] acest interval va fi spart în intervalele [2, 2], [3, 4], [5, 8], [9, 10], [11, 11].
Prezentăm procedura de construire a arborelui, implementată în java:
public void build_tree(int index, int low, int high) {
if (low == high) {
if (low != 0) aint[index] = new Node(low, high, a[low] - a[low - 1], a[low], a[low]);
else aint[index] = new Node(low, high, 0, 0, 0);
}
else {
aint[index] = new Node(low, high, -INFINIT, -INFINIT, INFINIT);
int mid = (low + high) / 2;
build_tree(2 * index, low, mid);
build_tree(2 * index + 1, mid + 1, high);
aint[index].maxS = Math.max(aint[2 * index].maxS,Math.max(aint[2 * index + 1].maxS,aint[2 * index + 1].max - aint[2 * index].min));
aint[index].max = Math.max(aint[2 * index].max,aint[2 * index + 1].max);
aint[index].min = Math.min(aint[2 * index].min,aint[2 * index + 1].min);
}
}Şi procedura care răspunde la întrebări tot în java:
long minPrefix;
int x, y;
public long queryTree(int index, int low, int high) {
if (x <= low && high <= y) {
long maxRet = aint[index].maxS;
if (minPrefix != infinity) {
maxRet = Math.max(maxRet, aint[index].max - minPrefix);
}
minPrefix = Math.min(minPrefix, aint[index].min);
return maxRet;
}
else {
int mid = (low + high) / 2;
if (x <= mid && mid < y) return Math.max(queryTree(2 * index, low, mid), queryTree(2 * index + 1, mid + 1, high));
else if (x > mid) return queryTree(2 * index + 1, mid + 1, high);
else return queryTree(2 * index, low, mid);
}
}Autorul vă recomandă articolele [1] şi [2] pentru o înţelegere mai profundă a structurii de date numită arbori de intervale. Problema poate fi soluţionată şi în O(N + M), dar algoritmul este mult prea complicat pentru un concurs de programare; cei interesaţi pot să îl găsească în [4].
Problema 4 ( ACM ICPC NWERC 97, olimpiada online 2000, campion 2001 )
Se dă un şir (a1, a2, ..., aN) format din numere întregi. Se cere să se determine subsecvenţa a[i..j] care are modulul sumei elementelor minim.
Exemplu
Pentru şirul (2, 8, -6, -6, 9, 4, -3), subsecvenţa este (4, -3), având suma în modul 1 = |4 - 3|.
Rezolvare
Facem mai întâi şirul sumelor parţiale. Pentru oricare două elemente sum[i] şi sum[j] ($i != j$) modulul sumei unei subsecvenţe din şir va fi |sum[i] - sum[j]|. Dacă i < j, atunci secvenţa va fi a[i+1..j], iar dacă j < i, atunci secvenţa va fi a[j+1 .. i]. Astfel, pentru a găsi subsecvenţa de modul minim trebuie, de fapt, să găsim perechea de indici i şi j astfel ca |sum[i] - sum[j]| să fie minim. Sortând şirul sumelor parţiale şi luând o pereche de indici i < j, atunci sum[i] < sum[j], iar |sum[j] - sum[i]| = sum[j] - sum[i]. Pentru a găsi perechea (i, j) pentru care i < j şi sum[j] - sum[i] este minim, trebuie ca i să fie egal cu j + 1. Astfel obţinem un algoritm de complexitate O(N log N).
Să vedem cum merge pe exemplul prezentat:
| a | - | 2 | 8 | -6 | -6 | 9 | 4 | -3 |
|---|---|---|---|---|---|---|---|---|
| sum | 0 | 2 | 10 | 4 | -2 | 7 | 11 | 8 |
| ind | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
În şirul ind vom păstra indicii reali ai sumelor parţiale. După sortare avem:
| sum | -2 | 0 | 2 | 4 | 7 | 8 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|
| ind | 4 | 0 | 1 | 4 | 5 | 7 | 2 | 6 |
O secvenţă de modul 2 ar fi cea reprezentată de sumele 8 şi 10, cu indicii 7 şi 2. Această secvenţă este (-6, -6, 9, 4, -3). Observăm ca cea mai mică diferenţă între termeni consecutivi e cea dintre 8 şi 7, care au indicii 7 şi 5, de unde obţinem că subsecvenţa de modul minim este (4, -3).
Problema 5 ( USACO )
Se dă un şir (a1, a2, ..., aN) format din N (1 <= N <= 100 000) numere întregi ($1 <= ai <= 2 000$). Se cere să se determine subsecvenţa a[i..i + K - 1] cu media aritmetică a elementelor maximă ( K >= F, 1 <= F <= N).
Exemplu
Pentru şirul (6, 4, 2, 10, 3, 8, 5, 9, 4, 1) şi F = 6 soluţia optimă este (10, 3, 8, 5, 9, 4), cu media 6.5.
Rezolvare
Fie X un număr real. Considerând şirul b, obţinut prin transformarea bi = ai - X, atunci toate subsecvenţele şirului b vor avea valoarea mediei elementelor lor cu X mai mică decât valoarea subsecvenţelor corespunzătoare din şirul a. Observăm apariţia a trei cazuri:
- Dacă subsecvenţa de sumă maximă din b are valoarea mai mare ca 0, atunci şi media ei va fi mai mare ca 0. Rezultă astfel că şi media subsecvenţei corespunzătoare din şirul a va fi mai mare decât X, deci media maximă a unei subsecvenţe din a va fi mai mare ca X.
- Cand subsecvenţa de sumă maximă din şirul b are media mai mică decât 0, atunci orice subsecvenţă din şirul a va avea media mai mică decât X.
- În cazul în care subsecvenţa de sumă maximă a şirului b are valoarea egală cu zero, atunci subsecvenţa de medie maximă a şirului a are media X.
Astfel putem face o căutare binară pentru a determina valoarea X a mediei maxime. Ne mai rămâne să determinăm un algoritm eficient pentru găsirea subsecvenţei de sumă maximă de lungime cel puţin F. O asemenea soluţie urmăreşte una din ideile din prima problemă: fie best[i] subsecvenţa de sumă maximă ce se termină în a[i]. Evident best[i] = max(a[i], best[i - 1] + a[i]). Acum secvenţa de sumă maximă ce se termină în a[i], de lungime cel puţin F se găseşte ca a[i] + a[i - 1] + .. + a[i - F + 2] + best[i - F + 1]. Această relaţie poate fi calculată în O(1) dacă ne folosim de trucul sumelor parţiale. Complexitatea finală este O(N log C), unde C e valoarea maximă a lui ai.
Problema 6 (Secvenţă)
Gigel are un şir de N numere întregi. Toată lumea ştie că o secvenţă este un subşir de numere care apar pe poziţii consecutive în şirul iniţial. Gigel a definit baza unei secvenţe ca fiind minimul valorilor elementelor din secvenţa respectivă. Fiind dat un număr natural K, determinaţi pentru Gigel o secvenţă de lungime cel puţin K, cu baza maximă. ( 1 <= K <= N <= 500 000)
Exemplu
Pentru K = 3 şi şirul (-1, 2, 3, 1, 0, 4, 8, 6), secvenţa de bază maximă este (4, 8, 6).
Rezolvare:
Presupunem că orice secvenţă optimă ar avea lungimea mai mare decât K. Atunci putem obţine o secvenţă mai mică, cu aceeaşi bază eliminând unul din capetele unei secvenţe optime. Deci este de ajuns să cautăm secvenţele optime de lungime exact K.
Acum putem face o parcurgere a şirului pentru a rezolva problema. Mai întâi punem într-un min-heap K elemente, verificăm vârful heapului şi obţinem astfel minimul secvenţei a[1..k]. Apoi eliminăm elementul a[ 1 ] din heap şi inserăm elementul a[K+1]. Prin verificarea vârfului heapului obţinem minimul secvenţei a[2..K+1]. Continuăm procedeul până aflăm elementul minim pentru fiecare subsecvenţă de lungime K a şirului a ( complexitate O(N log N) ). Există şi alte soluţii pentru găsirea elementului minim al unei subsecvenţe, precum folosirea unui arbore de intervale sau folosirea tehnicii O(n log n)/O(1) pentru problema RMQ, dar obţinem tot soluţii de complexitate O(N log N).
O observaţie importantă este aceea că dacă vrem să vedem minimul secvenţei ce se termină în i şi avem j1 < j2 <= i şi a[j1] >= a[j2], atunci evident a[j1] nu va fi minimul secvenţei ce se termină în i. Folosim o structură de date ca la soluţia cu heapuri, care adaugă elemente noi şi şterge elemente vechi, dar pe lângă elementele ce au fost inserate acum k paşi şi trebuie şterse, mai ştergem şi elementele mai noi care nu ne vor mai fi utile, după cum este a[j2] mai sus. Ca structură de date folosim o listă în care putem insera şi şterge de la ambele capete ( deque ). Fiecare element inserat în deque va fi o pereche de valori, valoarea din şir şi indexul din şir (a[i], i). Când o valoare este inserată în şir, ea este pusă la capătul din dreapta al şirului, dar înainte de inserare cât timp elementul din capătul şirului are valoarea mai mare decât a[i] el este eliminat. La fiecare pas după o inserţie se verifică dacă elementul din capătul din stânga este mai bătrân de K iteraţii.
Din cauza modului în care se fac inserţiile şi ştergerile, şirul va fi sortat totdeauna crescător după indecşi şi crescător după valori. Tot timpul ultimul element din stivă va conţine valoarea bazei. Acest algoritm are complexitatea O(N) pentru că fiecare element este inserat şi şters din deque cel mult o dată.
Să vedem cum funcţionează rezolvarea pe un exemplu : a = (-1, 2, 3, 1, 0, 4, 8, 6)
- inserăm (-1, 1)
lista devine: (-1, 1)
- inserăm (2, 2)
lista devine: (-1, 1) (2, 2)
- inserăm (3, 3)
lista devine: (-1, 1) (2, 2) (3, 3)
elementul minim al secvenţei a[1..3] este -1
- inserăm (1, 4)
ştergem (3, 3) şi (2, 2)
ştergem (-1, 1) ( inserat acum 4 paşi )
lista de vine: (1, 4)
elementul minim al secvenţei a[2..4] este 1
- inserăm (0, 5)
ştergem (1, 4)
lista devine: (0, 5)
elementul minim al secvenţei a[3..5] este 0.
- inserăm (4, 6)
lista devine: (0, 5) (4, 6)
elementul minim al secvenţei a[4..6] este 0
- inserăm (8, 7)
lista devine: (0, 5) (4, 6) (8, 7)
elementul minim al secvenţei a[5..7] este 0
- inserăm (6, 8)
ştergem (8, 7)
ştergem (0, 5) ( inserat acum 4 paşi )
lista devine: (4, 6) (6, 8)
elementul minim al secvenţei a[6..8] este 4
Problema 7 ( Agricultura - Algoritmus )
Vasilica vrea să se apuce de agricultură şi, prin urmare, să cumpere o parcelă de teren. Harta pusă la dispoziţie de către primăria oraşului în care locuieşte Vasilică se poate reprezenta sub forma unei matrice de dimensiuni NxM (2 <= N, M <= 150), fiecare m2 de teren fiind reprezentat printr-un element din matrice. Pentru fiecare m2 de pământ se cunoaşte altitudinea (faţă de nivelul mării) la care se află acesta. Agricultorul nostru doreşte să cumpere o parcelă de formă dreptunghiulară dar, deoarece are de gând să se ocupe de culturi foarte pretenţioase la modificări de nivel, diferenţa dintre valorile care indică altitudinea maximă şi cea minimă din parcelă trebuie să fie mai mică decât o valoare dată K (1 <= K <= 1 000). Mai mult, suprafaţa pe care Vasilică o va achiziţiona trebuie să fie cât mai mare posibil.
Exemplu
De exemplu pentru K = 3 şi matricea ![\[ \left( \begin{array}{cccccc}1 & 1 & 3 & 1 & 2 & 7 \9 & 2 & 3 & 2 & 3 & 2 \7 & 8 & 2 & 3 & 1 & 5 \4 & 5 & 6 & 0 & 1 & 4 \end{array} \right)\] \[ \left( \begin{array}{cccccc}1 & 1 & 3 & 1 & 2 & 7 \9 & 2 & 3 & 2 & 3 & 2 \7 & 8 & 2 & 3 & 1 & 5 \4 & 5 & 6 & 0 & 1 & 4 \end{array} \right)\]](http://www.infoarena.ro/static/images/latex/54365b052e7e35f363861774675094e5_22.50023pt.gif) , soluţia optimă va avea 9 celule.
, soluţia optimă va avea 9 celule.
Rezolvare:
Problema constă în determinarea submatricei cu număr maxim de celule în care diferenţa între valoarea maximă şi valoarea minimă este mai mică decât K. Vom folosi ideea de la problema cu subsecvenţa de sumă maximă pe matrice, adică vom fixa două linii i1 şi i2. Acum pentru fiecare coloană j păstrăm în m[j] elementul minim şi în M[j] elementul maxim a[i][j] cu i1 <= i <= i2. Astfel la fiecare pas trebuie acum să rezolvăm problema determinării unei subsecvenţe de lungime maximă pentru care diferenţa între elementul maxim şi minim este mai mică decât K. Folosind un max-heap şi un min-heap putem parcurge elementele şirurilor M şi m în ordine inserând la fiecare pas elemente în heap şi determinând cea mai lungă secvenţă ce se termină în i cu proprietatea dată. Vom ţine un al 2-lea indice j, iniţial 0, care atâta timp cât diferenţa între elementul maxim din max-heap cu elementul minim din min-heap este mai mare sau egală cu K, vom scoate din heapuri elementele M[j], respectiv m[j] şi îl vom incrementa pe j ( complexitate O(N3 log N) ). Dacă în loc de heapuri folosim deque-uri, atunci acest algoritm va avea complexitatea O(N3).
Problema 8 ( Secvenţa 2 )
Gigel s-a decis să devină olimpic la informatică, poate aşa va reuşi să-şi rezolve singur problemele, şi nu va mai cere ajutorul vostru! La ora de informatică, profesoara lui i-a dat să rezolve problema secvenţei de sumă maximă: "Gigele, eu iţi dau un şir de N numere întregi, iar tu trebuie să găseşti o secvenţă ( adică un subşir de numere care apar pe poziţii consecutive în şirul iniţial ) cu suma elementelor maximă!". După vreo 30 de minute, Gigel s-a ridicat mândru şi a zis: "Am găsit algoritmul de complexitate optimă, doamna profesoară!". Ca temă pentru acasă Gigel are de rezolvat aproape aceeaşi problemă: trebuie să găsească secvenţa de sumă maximă de lungime cel puţin K (1 <= k <= N <= 50 000). Gigel încă nu ştie destul de multă informatică ca să poata rezolva această problemă, dar poate îl ajutaţi voi! Scrieţi un program care rezolvă problema din tema lui Gigel.
Exemplu
De exemplu pentru şirul (0, -6, 2, 1, 4, -1, 3, -5) şi K = 3, soluţia optimă este (2, 1, 4, -1, 3).
Rezolvare:
Putem folosi rezolvarea liniară bazată pe programare dinamică prezentată ca subalgoritm în soluţia problemei 5, dar putem simplifica logica din acea rezolvare. Vom folosi şirul sumelor parţiale sum, iar pentru a determina subsecvenţa de sumă maximă ce se termină în i şi are lungimea cel puţin K trebuie să găsim sum[j] minim astfel ca j < i - K. Parcurgem lista, şi la pasul i determinăm best[i] = sum[i] - min(sum[j]), j < i - K. Comparăm minimul curent cu sum[i-K] şi trecem la pasul următor ( complexitate O(N) ).
Problema 9 ( Sum - Stelele Informaticii 2003 )
Se dă un şir de numere întregi. Se caută un subşir cu lungimea cuprinsă între L şi U, format din elemente consecutive ale şirului iniţial, cu suma elementelor maximă (1 <= L <= U <= N <= 100 000).
Rezolvare:
Pentru fiecare i este de ajuns să aflăm valoarea expresiei sum[i] - sum[j], unde i - L > j >= i - U. Pentru a determina valoarea optimă pentru sum[j] putem folosi un heap de dimensiune U - L, sau putem folosi tehnici de determinare a valorii minime într-un interval dat ( complexitate O(N log (U - L) ) ).
Altă abordare de aflare a minimelor unor secvenţe de lungime dată (în cazul acesta lungimea este U - L ) a fost prezentată în rezolvarea problemei 6. Folosind acea tehnică obţinem o rezolvare de complexitate liniară.
O altă rezolvare frumoasă prezentată în [4] este următoarea: Spunem că o secvenţă este negativă spre stânga dacă suma oricărui prefix ( în afară de secvenţa în sine ) al secvenţei este negativ sau zero. O partiţie a secvenţei A = (A1,A2,...,Ak) este minimală negativă spre stânga dacă fiecare Ai este negativă spre stânga, iar suma elementelor lui Ai este strict pozitivă dacă i != k. De exemplu secvenţa (-4, 1, -2, 3) este negativă la stânga, pe când secvenţa (5, -3, 4, -1, 2, -6) nu este. Partiţia (5) (-3, 4) (-1, 2) (-6) este minimală negativă la stânga.
Pentru fiecare element din partiţie ţinem minte un pointer p[i] spre ultimul element din subsecvenţa din care face parte. Fiecare interval (i, p[i]) va corespunde celei mai scurte subsecvenţe care începe în i şi are suma pozitivă. Pentru a determina o soluţie a problemei pentru fiecare i din care poate începe o subsecvenţă de sumă maximă, ne vom plimba cu un pointer j astfel ca j să fie cât mai depărtat de i şi j - i + 1 <= U. Obţinem astfel de fiecare dată o subsecvenţă de sumă maximă ce începe în i, cu lungimea mai mică sau egală cu U. Indicele j va fi întotdeauna un capăt de secvenţă negativă la stânga şi la fiecare mărire a lui i verificăm dacă lui j îi putem atribui valoarea p[j+1] ( adică dacă p[j+1] - i + 1 <= U ). Dacă secvenţa de sumă maximă de lungime cel mult U ce începe în i are lungimea mai mică decât L, atunci secvenţa de sumă maximă cu lungimea cuprinsă între L şi U are lungimea exact L ( complexitate O(N) ).
Problema 10 ( Secvenţa 3)
Gigel este o persoană cu o imaginaţie foarte bogată, mai ales când doarme! Într-o noapte a visat că are de îndeplinit o sarcină foarte bizară: trebuie să aleagă o secvenţă (adica un subşir de elemente care apar pe poziţii consecutive în şirul iniţial) din N elemente pentru care se cunosc costul şi timpul. Secvenţa aleasă trebuia să fie de lungime minim L şi maxim U, iar suma costurilor elementelor secvenţei împărţiţă la suma timpurilor elementelor secvenţei să fie maximă (1 <= L <= U <= N <= 30 000).
Exemplu
Pentru L = 1, R = 2 şi şirurile c = ( 1, 1, 3, 2, 5 ) şi t = ( 4, 2, 5, 3, 6 ), subsecvenţa cea mai eficientă are costul 0.83.
Rezolvare:
Procedăm ca la problema 5 şi căutăm binar valoarea optimă. Şirul va fi transformat în b[i] = c[i] - t[i]*X. Acum trebuie să mai rezolvăm subproblema care cere să determinăm o subsecvenţă de sumă maximă pentru care lungimea se află între L şi U. Această subproblemă a fost soluţionată în problema anterioară, unde s-a găsit un algoritm liniar. Astfel soluţia acestei probleme are complexitatea O(N log C).
Problema 11 ( XorMax )
Paftenie este un elev eminent. De multe ori îşi pune întrebări care au sau nu răspunsuri. De data aceasta i-a venit o idee nouă. El are un şir de N numere întregi nenegative şi vrea să aleagă o secvenţă a şirului (ai, ai+1, ..., aj) astfel încât ai xor ai+1 xor ... xor aj să fie maxim ( 1 <= N <= 100 000, numerele şirului sunt strict mai mici decât 221 ).
Exemplu
Pentru şirul (1, 0, 5, 4, 2), secvenţa cu valoarea sumei xor maximă este (4, 2), cu suma 6.
Rezolvare:
Suma xor a două numere este de fapt adunare binară fără transport, fapt care o face similară operaţiei modulo. Problema e asemănătoare cu cea a subsecvenţei de modul maxim. Vom obţine toate sumele xor parţiale şi pentru a vedea pentru sum[i] perechea optimă cu care crează o sumă cât mai mare trebuie să găsim acea sumă sum[j] astfel că fiecare bit al lui sum[i] să fie diferit de fiecare bit al lui sum[j], dacă acest lucru este posibil. Pentru a face această căutare cât mai eficientă, putem menţine sumele sum[i] ca şiruri de caractere 0 sau 1 într-un trie [5]. Structura de trie pentru cazul când alfabetul are dimensiunea 2 este identică cu cea de heap. Această soluţie are complexitatea O(N log C).
Probleme propuse
Pentru a vă însuşi mai bine tehnicile învăţate în acest articol, autorul vă sugerează să rezolvaţi următoarele două probleme de pe situl infoarena:
- Problema 1: Balans
- Problema 2: Struţi
Bibliografie
1. Lica Dana, Arbori de intervale (Segment Trees), GInfo 15/4
2. Negruşeri Cosmin, Căutări Ortogonale, Structuri de date şi aplicaţii, GInfo 15/5
3. Takaoka T., Efficient Algorithms for the Maximum Subarray Problem by Distance Matrix Multiplication
4. Kuan Yu Chen, Kun Mao Chao, On the Range Maximum-Sum Segment Query
5. Yaw Ling Liu, Tao Jiang, Kun Mao Chao, Efficient Algorithms for Locating the Length-Constrained Heaviest Segments, with Applications to Biomolecolar Sequence Analysis
6. Vladu Adrian, Negruşeri Cosmin, Ginfo Noiembrie 2005
7. Cormen Th., Leiserson Ch., Rivest R., Introducere în algoritmi, editura Agora
