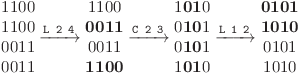| Fişierul intrare/ieşire: | polihroniade.in, polihroniade.out | Sursă | OJSEPI 2021, clasele 11-12 |
| Autor | Andrei Constantinescu | Adăugată de | |
| Timp execuţie pe test | 0.375 sec | Limită de memorie | 262144 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Polihroniade
 O matrice pătratică de dimensiuni N × N cu N par şi elemente din mulţimea {0, 1} se numeşte tablă de şah dacă oricare două celule vecine pe o linie sau pe o coloană au valori diferite (cu alte cuvinte, dacă nu există două valori egale alăturate).
O matrice pătratică de dimensiuni N × N cu N par şi elemente din mulţimea {0, 1} se numeşte tablă de şah dacă oricare două celule vecine pe o linie sau pe o coloană au valori diferite (cu alte cuvinte, dacă nu există două valori egale alăturate).
De ziua ei, Victor i-a cumpărat Elisabetei o astfel de matrice A, care nu este neapărat tablă de şah. Aflând despre pasiunea ei, acesta vrea acum să transforme matricea A într-o tablă de şah. Timpul fiind limitat, el poate efectua doar următoarele tipuri de operaţii asupra matricei:
- Interschimbă liniile i şi j din A (celelalte linii rămân neschimbate, iar valorile din interiorul liniilor i şi j rămân neschimbate şi îşi păstrează ordinea). Operaţia are sens pentru 1 ≤ i, j ≤ N .
- Interschimbă coloanele i şi j din A (celelalte coloane rămân neschimbate, iar valorile din interiorul coloanelor i şi j rămân neschimbate şi îşi păstrează ordinea). Operaţia are sens pentru 1 ≤ i, j ≤ N.
Dorind să o impresioneze pe Elisabeta, Victor apelează la voi, programatori renumiţi, să îl ajutaţi în a transforma matricea A într-o tablă de şah. Pentru aceasta, Victor are nevoie de următoarele informaţii:
- Poate fi transformată matricea A în tablă de şah?
- Care este numărul minim de operaţii necesare pentru a duce la îndeplinire acest scop?
- Care ar fi o succesiune de operaţii care transformă matricea A într-o tablă de şah?
În cazul ultimei cerinţe, pentru a intra în gratiile lui, Victor va trebui ca numărul de operaţii efectuate să fie minim. Totuşi, chiar şi un număr neminim de operaţii va fi răsplătit, însă nu într-atât de mult.
Vi se dau două numere P, T şi T matrice A, reprezentând mai multe instanţe ale problemei. Pentru fiecare matrice A dintre cele T va trebui să rezolvaţi cerinţa cu numărul P ∈ {1, 2, 3} dintre cele listate mai sus.
Date de intrare
Fişierul de intrare polihroniade.in va conţine pe prima linie două numere întregi pozitive P şi T, reprezentând numărul cerinţei de rezolvat şi, respectiv, numărul de scenarii pentru care va trebui să rezolvaţi problema.
Urmează cele T instanţe ale problemei, fiecare fiind compusă din N + 1 linii: pe prima linie se va afla numărul N, iar pe următoarele N linii câte N cifre binare neseparate prin spaţii, reprezentând câte o linie a matricei A.
Date de ieşire
În fişierul de ieşire polihroniade.out, pentru fiecare dintre cele T instanţe se va afişa răspunsul, începând de la o linie nouă, după cum urmează:
- Dacă P = 1, atunci se va afişa pe o singură linie 1 dacă matricea A poate fi transformată în tablă de şah, şi 0 altfel.
- Dacă P = 2, atunci se va afişa pe o singură linie un ı̂ntreg reprezentând numărul minim de interschimbări de linii şi/sau coloane necesare pentru a transforma matricea A în tablă de şah.
- Dacă P = 3, atunci se va afişa pe o linie un număr X. Apoi, pe fiecare dintre următoarele X linii se va afişa câte o interschimbare de linii sau coloane, după următorul format: L i j are semnificaţia că liniile i şi j se interschimbă, iar C i j are semnificaţia că coloanele i şi j se interschimbă. Matricea obţinută după aplicarea celor X operaţii asupra lui A în ordinea dată trebuie să fie o tablă de şah.
Restricţii
- 1 ≤ T ≤ 350
- 1 ≤ N ≤ 1 000
- N este par.
- Pentru cerinţele de tip P = 2 şi P = 3 se garantează că matricea A poate fi transformată ı̂n tablă de şah folosind interschimbări de linii şi/sau coloane.
- Suma valorilor N pentru cele T scenarii nu depăşeşte 2 000.
Pentru 40 de puncte
- P = 1
Pentru alte 34 de puncte
- P = 2
Pentru alte 26 de puncte
- P = 3
- Dacă există mai multe soluţii, oricare este considerată corectă.
- Dacă numărul X de operaţii folosite nu este minim, atunci se acordă 50% din punctajul pe test.
Exemple
| polihroniade.in | polihroniade.out |
|---|---|
| 1 3 2 11 11 4 1100 1100 0011 0011 2 10 01 | 0 1 1 |
| 2 2 4 1100 1100 0011 0011 2 10 01 | 2 0 |
| 3 2 4 1100 1100 0011 0011 2 10 01 | 3 L 2 4 C 2 3 L 1 2 0 |
Explicaţii
Pentru primul exemplu, avem P = 1, deci pentru cele T = 3 instanţe se cere numai dacă se pot transforma în tablă de şah prin interschimbări de linii şi/sau coloane. Pentru prima instanţă acest lucru nu este posibil, deoarece nu avem niciun 0 ı̂n matrice. Pentru cea de-a doua instanţă, putem efectua următoarele operaţii:
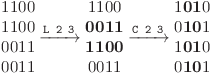
Pentru ultima instanţă, matricea A este deja tablă de şah. Pentru al doilea exemplu, avem P = 2, deci pentru cele T = 2 instanţe se cere numărul minim de operaţii pentru a le transforma în tablă de şah. Pentru prima instanţă, o solutie cu 2 operaţii este prezentată mai sus, şi nu există soluţii mai scurte. Pentru cea de-a doua instanţă, matricea este deja tablă de şah, deci răspunsul este 0.
Al treilea exemplu este exact ca anteriorul, numai că avem P = 3, deci trebuie tipărite exact care sunt operaţiile ce aduc matricea la forma de tablă de şah. Pentru punctaj maxim pe acest exemplu, ar fi obligatoriu să afişăm o soluţie cu 2 operaţii (adică număr minim), cum ar fi cea de mai sus. Cu toate acestea, cu scop demonstrativ, noi venim cu o soluţie compusă din 3 operaţii, prin care obţinem doar 50% din punctaj: