Fişierul intrare/ieşire:overpower.in, overpower.outSursăJunior Challenge 2019
AutorTheodor MoroianuAdăugată deJuniorChallenge2019Junior Challenge 2019 •JuniorChallenge2019
Timp execuţie pe test0.5 secLimită de memorie262144 kbytes
Scorul tăuN/ADificultateN/A

Vezi solutiile trimise | Statistici

Overpower

Cearta dintre liceul Unaiv si Institutia Teoretica de Informatica creste din ce in ce mai mult.
Apar argumente de tipul:

  • "La noi profesorii sunt mai ingaduitori cu elevii",
  • "Noi nici macar nu ne stim profesorii", sau
  • "La 'scoala altfel' ar trebui sa incercati sa faceti si voi ore".

Tahref, profesor remarcabil, extenuat de nesfarsita lupta dintre liceu si institutie, decide sa puna un sfarsit discordiei, prin spargerea sistemului de securitate din Unaiv si preluarea puterii (si asa Unaiv isi schimba directorii din 2 in 2 ani).
Pentru a se putea infiltra in sistemele liceului, Tahref trebuie sa resolve urmatoarea problema:

Puterea unui numar 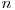n este valoarea maxima 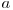a astfel incat 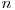n sa poata fi scris ca un produs a doi termini naturali, unul dintre cei doi diferit de 1 avand exponentul a.
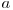Concret,
P($n$) = max($a$ \: \in N \quad a.i. \quad \exists \; $p$ \: si\: $q$ \in N ,\;$q$\neq 1 \quad cu \quad $n$ \:= \:$p$\; *\; {$q$}^a)

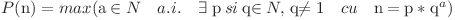
Puterea intervalului 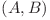(A, B) este max(P($A$), P($A$+1), . . ., P($B$))

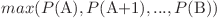
Se dau mai multe intervale, si pentru fiecare interval se cere puterea lui.

Date de intrare

Prima linie contine Q, numarul de intrebari.
Urmatoarele Q linii contin doua numere A si B, limitele intervalului.

Date de ieşire

Fisierul de iesire contine Q linii, a i-a linie continand raspunsul pentru al i-lea query.

Restricţii

  • Pentru a trece un test, trebuie ca raspunsul la toate intrebarile din acel test sa fie corect.
  • Testele sunt grupate. Pentru a lua punctajul unui subtask trebuie ca solutia sa treaca toate testele acelui subtask.
  • 1 ≤ Q ≤ 50
  • 2 ≤ A ≤ B ≤ 1018

Subtaskuri

  1. 10 puncte: 2 ≤ A ≤ B ≤ 100 (testul 1)
  2. 10 puncte: 2 ≤ A ≤ B ≤ 106 (testul 2)
  3. 20 de puncte: 2 ≤ A ≤ B ≤ 1012 (testele 3-4)
  4. 10 puncte: A = B, 2 ≤ A ≤ 1018 (testul 5)
  5. 50 de puncte: Restricţiile iniţiale (testele 6-10)

Exemplu

overpower.inoverpower.out
4
2 2
50 51
25 30
34 37
1
2
3
2
4
999999874000003969 999999874000003969
24839 45762
100000000000 2000000000000
2 2
2
15
40
1
3
10000000000 10000000000
29874019739018 29874019739020
1000 10000
10
2
13

Explicaţie pentru primul exemplu

Sunt 4 intrebari:

  • Primul interval contine numarul 2, care poate fi scris de forma 1 * 21, exponentul maxim fiind 1
  • Al doilea interval contine numarul 50 = 2 * 52, exponentul maxim fiind 2
  • Al treilea interval contine numarul 27 = 1 * 33, exponentul maxim fiind 3
  • Al patrulea interval contine numarul 36 = 1 * 62, exponentul maxim fiind 2
Trebuie sa te autentifici pentru a trimite solutii. Click aici

Cum se trimit solutii?