Fişierul intrare/ieşire:	imax.in, imax.out	Sursă	Lot Alba 2007
Autor	Dana Lica	Adăugată de	Adrian Diaconu •DITzoneC
Timp execuţie pe test	0.05 sec	Limită de memorie	20480 kbytes
Scorul tău	N/A	Dificultate	N/A

Vezi solutiile trimise | Statistici

IMax

Sa consideram o matrice binara cu n linii (numerotate de la 1 la n) si m coloane (numerotate de la 1 la m). in interiorul acestei matrice se pot distinge unul sau mai multe obiecte de tip "I".
Un obiect este considerat a fi de tip "I" daca:

• este format din trei subtablouri (zone de forma dreptunghiulara din matrice) alaturate pe verticala (sa le numim subtabloul de sus, subtabloul de mijloc si subtabloul de jos);
• cele 3 subtablouri contin numai valoarea 0;
• subtablourile pot fi identificate prin indicii elementelor ce reprezinta coltul stanga-sus, respectiv coltul dreapta-jos (pentru subtabloul de sus (l₁,c₁) (l₂,c₂), pentru subtabloul de mijloc (l₃,c₃) (l₄,c₄), iar pentru subtabloul de jos (l₅,c₅) (l₆,c₆)). Pentru ca obiectul sa respecte forma grafica a literei "I" trebuie sa fie respectate si relatiile urmatoare:
  • 1 ≤ l₁ ≤ l₂ < l₃ ≤ l₄ < l₅ ≤ l₆ ≤ n
  • l₃ = l₂ + 1
  • l₅ = l₄ + 1
  • 1 ≤ c₁ < c₃ ≤ c₄ < c₂ ≤ m
  • 1 ≤ c₅ < c₃ ≤ c₄ < c₆ ≤ m

Obiecte de tip "I" corecte	Obiecte ce nu sunt de tip "I"

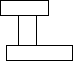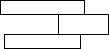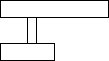Cerinta

Sa se determine aria maxima a unui obiect de tip "I". Aria unui obiect este egala cu numarul de elemente existente in cele 3 subtablouri ce constituie obiectul.

Date de intrare

Pe prima linie a fisierului imax.in se afla doua numere naturale separate prin spatiu n si m, cu semnificatia din enunt. Pe urmatoarele n linii se afla cate m valori din multimea {0, 1}, separate prin cate un spatiu, reprezentand elementele matricei.

Date de iesire

Fisierul de iesire imax.out va contine o singura linie pe care se va scrie aria maxima a unui obiect "I".

Restrictii

• 1 ≤ N ≤ 150
• 1 ≤ M ≤ 150

Exemplu

Explicatie

0 0 0 0
1 0 0 1
0 0 0 1
0 1 1 0

Cum se trimit solutii?