Revizia anterioară Revizia următoare
| Fişierul intrare/ieşire: | ctc.in, ctc.out | Sursă | Arhiva educationala |
| Autor | Arhiva Educationala | Adăugată de |  Marius Stroe •Marius |
| Timp execuţie pe test | 0.175 sec | Limită de memorie | 524288 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Poti vedea testele pentru aceasta problema accesand atasamentele.Vezi solutiile trimise | Statistici
Componente tare conexe
Se dă un graf orientat G = (V, E). O componentă tare conexă a grafului orientat G este o mulţime maximală de vârfuri U inclusă în V, astfel încât, pentru fiecare pereche de vârfuri u şi v din U avem atât drum de la u la v cât şi drum de la v la u. Cu alte cuvinte, vâfurile u şi v sunt accesibile unul din celălalt.
Cerinţă
Dându-se un graf orientat G = (V, E) se cere să se determine componentele sale tare conexe.
Date de intrare
Fişierul de intrare ctc.in conţine pe prima linie două numere naturale N, M ce reprezintă numărul de noduri din G şi numărul muchiilor. Pe următoarele M linii se vor afla câte două numere naturale x şi y, separate prin spaţiu, reprezentând muchia orientată (x, y).
Date de ieşire
În fişierul de ieşire ctc.out veţi afişa pe prima linie un singur număr reprezentând numărul componentelor tare conexe. Pe fiecare din următoarele linii se va scrie câte o componentă tare conexă prin enumerarea nodurilor componente. Ordinea lor poate fi oricum.
Restricţii
- 1 ≤ N ≤ 100 000
- 1 ≤ M ≤ 200 000
- Pentru 30% din teste: 1 ≤ N ≤ 100, 1 ≤ M ≤ 500
- Pentru 60% din teste: 1 ≤ N ≤ 5 000, 1 ≤ M ≤ 25 000
- Pentru aflarea corectă a numărului componentelor tare conexe se va acorda 40% din punctaj şi încă 60% pentru enumerarea corectă a lor.
Exemplu
| ctc.in | ctc.out |
|---|---|
| 8 12 1 2 2 6 6 7 7 6 3 1 3 4 2 3 4 5 5 4 6 5 5 8 8 7 | 2 1 2 3 4 5 6 7 8 |
Explicaţie
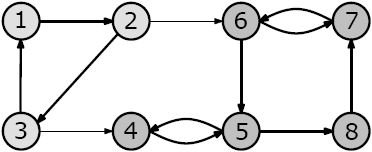
În graful orientat din exemplu componentele tare conexe sunt reprezentate cu nuanţe diferite de gri. Aici, 1 2 3 reprezintă prima componentă tare conexă, iar 4 5 6 7 8 cea de a doua.
