Solutii Junior Challenge 2020

• Lista de probleme
• Aparate
• Heist
• Plangaciosi

Soluţia problemei Aparate

Subtask 1 (10 puncte) - Q ≤ 1.000

Putem simula direct toate operaţiile cu brute-force. La un update, luăm toate coloanele şi le rotim în O(N) cu k poziţii, iar la un query luăm toate elementele de pe linia k cu coloanele de la l până la r şi le facem suma. Complexitatea pe un query este O(M), iar complexitatea unui update este O(N * M), deci complexitatea totală o să fie O(Q * N * M) pe cel mai rău caz.

Subtask 2 (20 puncte) - M ≤ 1.000

Putem să nu facem rotaţiile fizice şi să ţinem minte pentru fiecare coloană cu câte poziţii a fost rotită în sus. Dacă o coloană c a fost rotită în sus cu k poziţii, ca să accesăm elementul de pe linia l, putem defapt să accesăm din matricea iniţială elementul de pe linia (l + k) % N şi coloana c (cu precizarea că în soluţie indexăm liniile şi coloanele de la 0, nu de la 1).

La un update trebuie doar să actualizăm pentru fiecare coloană cu câte poziţii am rotit-o în sus, iar la un query putem direct să facem suma elementelor cerute.

Astfel complexitatea unui update devine O(M), iar complexitatea unui query devine tot O(M). Astfel, complexitatea finală o să fie O(Q * M).

Subtask 3 (30 puncte) - N = 2

Dacă N = 2, atunci M ≤ 50.000. La acest subtask avem două soluţii.

Prima ar fi să folosim un arbore de intervale pentru a simula operaţiile. Pentru fiecare nod din arborele de intervale (care ţine minte date despre intervalul de coloane [l, r]), trebuie să ţinem minte suma elementelor de pe linia 1 cu coloanele din intervalul respectiv, suma elementelor de pe linia 2 cu coloanele din intervalul respectiv, şi un lazy care să ne spună dacă trebuie să interschimbăm cele două linii pe care îl propagăm in fiii nodului. Această soluţie va avea complexitatea O(Q * logM).

O altă soluţie mai uşor de implementat ar fi să grupăm coloanele în grupe de câte B coloane. La un update, dacă o grupă este complet inclusă în intervalul respectiv, putem să ţinem minte ca şi la subtaskul 2 o valoare care să ne spună cu cât am rotit toate acele coloane din grupa respectivă. Dacă o grupă de coloane este doar parţial inclusă într-un update, putem să rotim fizic (ca şi la subtaskul 1) coloanele care sunt afectate de operaţie. Pentru fiecare grupă trebuie să menţinem şi sumele elementelor de pe fiecare linie. Ca să răspundem la un query luăm toate grupele: dacă o grupă este total inclusă, putem să facem ca şi la subtaskul 2, să vedem care este poziţia adevărată a liniei pe care o vrem, altfel dacă o grupă este inclusa parţial, atunci putem să luăm cu brut elementele din query. Complexitatea pentru un update sau un query va fi O(B * N + M / B). Deoarece N = 2, complexitatea finală va fi O(Q * (B * N + M / B)). Dacă fixăm B = sqrt(M), vom obţine complexitatea finală O(Q * sqrt(M)). 

Subtask 4 (40 puncte)

La momentul acesta avem foarte multe soluţii care se încadrează în limita de timp pe anumite clase de teste: soluţia de la subtaskul 2 merge bine pe testele cu M mic, dar iese din timp pe celălalte teste, prima soluţie de la subtaskul 3 merge pe teste cu M mare (dacă îl adaptăm să meargă pe teste cu N > 2 în complexitate O(Q * N * logM)), iar a doua soluţie de la subtaskul 3 merge bine pe testele cu M mare, dar merge prost pe teste cu M mic (asta dacă ne fixăm B la început ca şi o constantă, precum 300, 500 sau 420).

Putem să combinăm mai multe soluţii între ele pentru a obţine soluţii care să se încadreze în limita de timp.

Cum combinăm soluţiile între ele?

Dacă avem o complexitate de forma N * B + M / B, şi trebuie să ne alegem convenabil un B, cel mai eficient este să egalăm cei doi termeni şi să aflăm astfel B-ul. Astfel o să obţinem:
N * B = M / B <=>
B^2 = M / N => B = sqrt(M / N)
Varianta aceasta este optimă. Putem demonstra asta folosind inegalitatea mediilor care spune că (a + b) / 2 ≥ sqrt(a * b), iar egalitatea se obţine dacă a şi b sunt egale. Astfel, dacă înlocuim termenii cu expresia noastră iniţială, o să obţinem că (N * B + M / B) / 2 ≥ sqrt(N * M), deci (N * B + M / B) ≥ sqrt(N * M) care este o constantă. Deci dacă egalăm cei doi termeni (aşa cum am procedat mai sus), vom obţine complexitatea optimă.

Acuma putem să combinăm toate soluţiile între ele şi să vedem ce obţinem:

# Putem combina soluţia de la subtaskul 2 cu prima de la subtaskul 3
# Putem combina soluţia de la subtaskul 2 cu a doua de la subtaskul 3

Totuşi, din punct de vedere al implementării ar însemna să implementăm două soluţii independente şi ar ieşi mult mai greoi implementarea. În continuare vom analiza mai mult soluţia de la subtaskul 3.
Complexitatea soluţiei este O(Q * (N * B + M / B)). Dacă folosim formula de mai sus, vom obţine că B trebuie să fie sqrt(M / N). Complexitatea finală va fi O(Q * (N * sqrt(M / N) + M / sqrt(M / N))) = O(Q * sqrt(M * N)).

De menţionat că sqrt(M / N) poate fi mai mic decât 1. Cum nu putem fixa un bucket cu 0, putem folosi funcţia ceil() pentru a evita astfel de probleme. În cazul acesta, practic soluţia noastră care face mai multe bucketuri imită soluţia de la subtaskul 2.

Altă menţiune ar mai fi faptul că aici mărimea bucketului variază, şi este esenţial să avem grija de acest lucru şi să nu fixăm mărimea lui ca şi o constantă în cod.

Soluţia problemei Heist

Prima observaţie importantă este 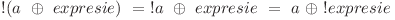că si ca 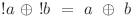. Aşadar ne dăm seama că orice expresie poate fi rescrisă fără semne de negaţie sau cu un singur semn de negaţie, în funcţie de paritatea numărului semnelor de negaţie care apar în expresia iniţială.

Cum operaţia xor e asociativă şi comutativă şi 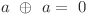, putem scrie orice expresie fără paranteze şi fiecare variabilă să apară fie o dată, fie deloc. Astfel singurele expresii pe care trebuie să le luăm în considerare sunt cele cu maxim variabile în care putem avea maxim un semn de negaţie. În total sunt 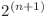astfel de expresii deci dacă le-am genera pe toate şi le-am evalua cu un backtracking, complexitatea finală ar fi 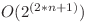, o soluţie care dacă este suficient de bine optimizată poate să ia 60 de puncte.

Ne dăm seama că dacă pe prima poziţie din şirul de biţi apare , atunci semnul de negaţie apare neapărat. La fel dacă pe prima poziţie din şirul de biţi apare , atunci nu avem semn de negaţie. Astfel putem determina în 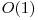dacă avem negaţie sau nu. Dacă avem negaţie, putem nega întreg şirul de biţi şi putem rezolva problema la fel ca în cazul în care nu avem negaţie. Mai departe rezolvăm problema când nu avem negaţie.

Dacă indexăm şirul de biţi de la , ştim că bitul de pe poziţia 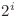, unde 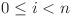, îi corespunde valorii expresiei atunci când toate variabilele mai puţin variabila cu ordinul 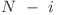sunt egale cu . Dacă bitul de pe poziţia 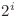are valoarea înseamnă că variabila nu apare în expresie, iar dacă are valoarea înseamnă că variabila apare în expresie. Astfel am determinat în 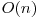o expresie posibil validă. Trebuie să verificăm dacă expresia determinată este corecta, asta fiind foarte uşor cu un backtracking de complexitate 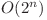, soluţie care obţine 100 de puncte.

Soluţia problemei Plangaciosi

O primă observaţie este că pentru a rezolva problema trebuie să aflăm câte secvenţe de alegeri există pentru fiecare lungime posibilă.

Subtaskul 1

Când numărul de secvenţe posibile este cel mult 2 * 10⁶, problema poate fi rezolvată prin backtracking, generând toate secvenţele posibile.

Subtaskul 2

Când A_i = 1, pentru orice i, numărul de secvenţe de alegeri de lungime L este combinari(N, L) * L.

Subtaskul 3

Putem fixa, pe rând, tortul din care şi-ar dori să manânce PlângăciosulNr1. Fie acesta tortul x.
Vom folosi programarea dinamică pentru a calcula dp[i][j] = în câte moduri putem alege j felii, considerând doar primele i torturi, astfel încât în fiecare tort să rămână un număr nenegativ de felii, iar din tortul x să nu fie luată nicio felie.
Recurenţa pentru i != x este: dp[i][j] = suma (dp[i-1][j-t] * combinari(j, t)), unde 0<=t<=a[i]
Recurenţa pentru i = x este: dp[i][j] = dp[i-1][j]
Apoi, putem calcula cnt[x][i] = câte secvenţe de alegeri se termină cu tortul x şi au lungimea i.
cnt[x][i] = dp[n][i - a[x]] * combinari(i, a[x]).
Obţinem complexitatea O(N * S²), unde S = sumă(A_i).

Subtaskul 4

Putem îmbunătăţi soluţia anterioară observând că dacă torturile x şi y au acelaşi număr de felii, atunci cnt[x][i] = cnt[y][i], pentru orice i. Astfel, putem rula dinamica anterioară câte o dată pentru fiecare valoare distinctă din A. În total, sunt cel mult sqtr(2*sum(A_i)) valori distincte. Obţinem complexitatea O(S² * sqrt(S)).

Subtaskul 5

Vom construi o altă dinamică, D[i][j][0/1] = în câte moduri putem alege j felii, considerând doar primele i torturi, astfel încât în fiecare tort să rămână un număr nenegativ de felii. A treia dimensiune poate fi 0 sau 1, specificând dacă tortul din care şi-ar dori să manânce PlângăciosulNr1 se află între primele i torturi. Recurenţa este:

D[i][j][ 0 ] = suma (D[i-1][j-t ][ 0 ] * combinari(j, t)), unde 0<=t<=a[i]
D[i][j][ 1 ] = D[i-1][j-a[i]][ 0 ] * combinari(j, a[i]) + suma (D[i-1][j-t][ 1 ] * combinari(j, t)), unde 0<=t<=a[i]

Complexitatea acestei soluţii este O(S²).