Solutii Selectie Girls Programming Camp 2011

Crescator

Pentru a rezolva prima cerinţă a problemei este necesar să determinăm lungimea fiecărei subsecvenţe crescătoare maximale din şir, unde prin secvenţă crescătoare maximală înţelegem o secvenţă crescătoare ce nu mai poate fi extinsă spre stânga sau dreapta. Pentru fiecare astfel de lungime x determinată, vom aduna la soluţie valoarea x*(x+1)/2, deoarece orice subsecvenţă a unei subsecvenţe crescătoare maximale este o subsecvenţă crescătoare. Pentru a determina aceste valori x, este suficient să parcurgem şirul de la stânga la dreapta şi să tratăm următoarele situaţii:

dacă A[i - 1] < A[i], incrementăm x cu o unitate
altfel, adunăm x*(x+1)/2 la soluţie şi reiniţializăm x cu 0.

Pentru a rezolva cerinţa a doua este suficient să reţinem valoarea x maximă ce o vom întâlni în timpul parcurgerii. Complexitate finală 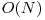$O(N)$ .

Nivele2

Se face o parcurgere dfs / bfs în care se reţine într-un vector dp[x] = nivelul la care este nodul x. Acesta se actualizează în cadrul parcurgerii, iar în plus de asta se ţine un vector soluţie sol în care reţinem pentru fiecare nivel în parte nodurile acestuia. El se actualizează tot în cadrul parcurgerii, bagând la fiecare pas în sol[dp[x]] nodurile pe care le gasim "pe drum". Uite un pseudocod pentru o parcurgere dfs :

procedura dfs (int nod) {
    pentru fiecare vecin x a lui nod executa 
        daca dp[x] = 0 atunci
            dp[x] := dp[nod] + 1
            adauga la sol[dp[x]] nodul x
            dfs (x)
}

Complexitatea finala 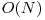$O(N)$ .

Magic Numbers

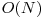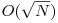Dificultatea acestei probleme a constat în determinarea numărului de divizori pentru fiecare număr dintr-un interval de numere întregi. Acest lucru s-ar fi putut rezolva parcurgând fiecare număr între X şi Y şi aflându-i numărul de divizori în complexitate $O(N)$ sau $O(\sqrt{N})$ . Aceste soluţii ar fi obţinut 30, respectiv 60 de puncte.

Pentru a obţine 100 de puncte este necesară folosirea ciurului lui Eratostene (citiţi acest articol pentru mai multe detalii). Folosim un vector V de dimensiune 2 000 000 pentru a reţine numărul de divizori pentru fiecare număr din intervalul [1, Y]. Apoi fixăm fiecare divizor posibil i din intervalul [1, Y] şi incrementăm cu 1 valorile din V din i in i. Apoi, pentru a afla rezultatul căutat, parcurgem numerele aflate între X şi Y şi testăm câte dintre acestea sunt magice folosind vectorul V. Complexitatea timp totală a acestei soluţii este 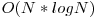$O(N * logN)$ .

Pescari

Această problema se rezolvă cu Algoritmul lui Lee. Se introduc toate porţiunile acoperite de apă într-o coadă şi se aplică acest algoritm, obţinându-se o matrice în care dist[i][j] = distanţa de la punctul (i, j) la cea mai apropiată porţiune de apă. În final, se parcurge în ordine această matrice şi în momentul în care am dat de un pescar, afişăm dist[i][j]. Complexitatea finală 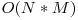$O(N * M)$ .

Transformari

Soluţia problemei se bazează pe două observaţii:

Orice pereche (X, Y) ce poate fi obţinută prin aplicarea unui şir de transformări are proprietatea că cmmdc(X, Y) = 1.
Orice pereche (X, Y) cu cmmdc(X, Y) = 1 poate fi obţinută prin aplicarea a unui singur şir de transformări.

Prima observaţie poate fi demonstrată inductiv. Considerăm o pereche (X, Y) cu X şi Y prime între ele. Luăm un divizor d al lui X şi fie r restul împărţirii lui Y la d. În mod evident r ≠ 0. Restul împărţirii numarului X + Y la d va fi ((X mod d) + (Y mod d)) mod d = (0 + r) mod d = r . Deci noul numar obţinut va fi de asemenea prim cu X. El va fi prim şi cu Y în mod analog. Perechea (1 , 1) respecta proprietatea în mod evident.

A doua observaţie este evidentă iar demonstraţia ei poate fi dedusă uşor de cititor.

Avand aceste observaţii, putem căuta un algoritm care să încerce toate valorile X mai mici decat N şi să testeze numărul de paşi necesari pentru a obţine perechea (X, N). Observăm că aplicând transformarea "inversă" unei perechi, procesul este identic cu cel desfăşurat de Algoritmul lui Euclid prin scăderi. Avem acum o soluţie de complexitate totală 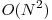$O(N^2)$ care însă nu este fezabilă pentru cazul dat. Pentru a ajunge la o complexitate de 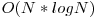$O(N * logN)$ vom folosi Algoritmul lui Euclid prin împărţiri, modificat astfel încât să numere de câte scăderi ar fi fost nevoie pentru a ajunge la perechea (1, 1).

int ret (int n, int x) {
    if (x == 1) 
        return n - 1; // Daca am ajuns la o pereche de forma (n , 1) mai avem nevoie de n - 1 pasi.
	
    if (x == 0)
	    return inf; // Ajungem in aceasta situatie daca numerele nu sunt prime intre ele, caz in care codul intoarce o valoare suficient de mare incat sa nu fie luata in calcul in cautarea minimului 
    return n / x + ret (x , n % x); //  Sunt necesare n / x scaderi ale lui x din n pentru a ajunge in starea (x , n % x).
}

Simetrii

Se observă ca e suficientă o translaţie şi o rotaţie în cazul în care avem soluţie. Se mai observă ca rotaţia o facem doar faţă de origine (0, 0). Aşadar, pentru fiecare rotaţie faţă de origine cu 0, 90, 180, 270 grade verificăm dacă putem translata punctele rotite pentru a obţine setul B. Acest lucru îl facem adăugând la setul de puncte noi rotite diferenţa pe componente dintre primul punct din B şi primul punct din acest set, adică fiecare punct din setul curent va deveni (x + diffx, y + diffy), unde diffx este diferenţa dintre B₁.x şi SC₁.x (unde cu SC am notat setul curent), şi analog diffy. Pentru a face toate aceste operaţii optim, se vor sorta punctele din B, şi punctele din SC (la fiecare rotaţie în parte). Pentru a roti cu 90 grade, fiecare punct (x, y) va deveni punct de coordonate (-y, x). Pentru rotirea cu 180 sau cu 270 grade, se roteşte de 2, respectiv de 3 ori cu 90 grade.

sorteaza (B)
pentru fiecare rotatie cu un unghi alfa (0, 90, 180, 270) executa
    set_puncte SC = A
    sorteaza (SC)
    punct aux = (B[1].x - SC[1].x, B[1].y - SC[1].y)
    translateaza SC cu aux
    sorteaza (SC)
    daca SC = B scrie solutie (rotatie cu unghiul alfa si translatie cu aux)

Astfel, se obţine o complexitate teoretică 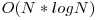$O(N * logN)$ .

Edist

Problema distanţei de editare este o problema clasică de programare dinamică care poartă numele de Distanţa Levenshtein. Soluţia clasică, în complexitate timp 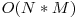$O(N * M)$ , presupune calculul matricei dp[i][j] = numărul minim de operaţii ce trebuie efectuare asupra primelor i caractere din primul şir pentru a obţine primele j caractere din al doilea şir. Recurenţa este dp[i][j] = min{ dp[i-1][j] + 1, dp[i][j-1] + 1, dp[i-1][j-1] + eval(i, j) }, unde eval(i, j) returnează 1 dacă al i-lea caracter din primul şir este diferit de cel de-al j-lea caracter din al doilea şir şi 0 în caz contrar. Dinamica se iniţilizează cu dp[i][ 0 ] = dp[ 0 ][i] = i, iar rezultatul căutat se află în dp[N][M]. Restricţia suplimentară că distanţa de editare a celor două şiruri este ≤ K poate fi folosită pentru a micşora numărul de celule calculate în dinamica clasică. Mai exact, pentru o linie i oarecare a matricii dp este suficient să calculăm celulele a căror coloană se află între i - K şi i + K, deoarece celulele aflate în afara acestui interval reprezintă şiruri pentru care diferenţa lungimilor este > K şi deci cel puţin K + 1 inserări sau ştergeri ar fi necesare pentru a transforma primul şir în cel de-al doilea. Se poate micsora si memoria necesara folosita observand ca in matrice nu folosim decat linia i-1 si i. Astfel se poate aplica distanta Levenshtein folosind numai doi vetori, memoria transformandu-se din 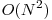$O(N^2)$ in $O(N)$ .
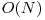Folosind aceste optimizări, complexitatea timp a rezolvării devine 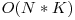$O(N * K)$ .

Eveniment sponsorizat de Facebook