021 Invers modular

[•filipb]

Aici puteti discuta despre problema Invers modular.

[•philip]

Nu inteleg cum se calculeaza numarul de combinari. Daca stiti alt loc in care e explicata chestia asta, va rog sa postati linkul aici.

[•pauldb]

Daca puterea la care apare P in N! este mai mare care puterea la care apare in K!*(N-K)!, atunci raspunsul e 0 (rezultatul e divizibil cu P).

Altfel, calculezi a = N! % P, b = K! % P si c = (N-K)! % P, fiecare in O(N). Rezultatul e (a * b^-1*c^-1) % P, unde b^-1 e inversul modular a lui b fata de P, iar c^-1 e inversul modular a lui c fata de P.

[•philip]

Asa da... e mai pe intelesul meu.
Abia acum am inteles si ce e de fapt inversul modular.

[•popoiu.george]

Am inteles ce este inversul modular, dar am cateva nedumeriri.

Pentru orice numar N>=P, N! % P este automat egal cu 0. Este asa sau gresesc ?

Cum mai calculez inversul modular daca a, b sau c pot fi 0.

Terenul asta e intr-un fel "minat" pentru mine, pt ca nu am cunostinte solide de aritmetica modulara.

Multumesc !

[•alexandru92]

Pentru orice numar N>=P, N! % P este automat egal cu 0. Este asa sau gresesc ?

Da, si este simplu de justificat. N!=1*2*3*...*N, daca N >= P N!=1*2*3*...*P*...*N => N! este un multiplu de P, deci N! se imparta exact la P.

Terenul asta e intr-un fel "minat" pentru mine, pt ca nu am cunostinte solide de aritmetica modulara.

Poate te ajuta asta.

[•SpiderMan]

Se poate adauga la aplicatii si problema LKperm.

[•razyelx]

Daca puterea la care apare P in N! este mai mare care puterea la care apare in K!*(N-K)!, atunci raspunsul e 0 (rezultatul e divizibil cu P).

Altfel, calculezi a = N! % P, b = K! % P si c = (N-K)! % P, fiecare in O(N). Rezultatul e (a * b^-1*c^-1) % P, unde b^-1 e inversul modular a lui b fata de P, iar c^-1 e inversul modular a lui c fata de P.

daca N are valoarea 1000 cum calc fact? fac modulo n la un anumit interval de elemente?

[•dutzul]

hmm am citit despre teorema lui euler  si egaliatea aia a^(phi(n))=1 dar aceasta egalitate are loc doar cand n si a sunt prime intre ele .Daca au un divizor comun != 1 nu mai e valabila asta inseamna ca nu se poate afla inversul numarului? mersi anticipat

[•PlayLikeNeverB4]

In cel mai rau caz incerci fiecare numar pana gasesti inversul (adica brute).

[•klamathix]

Inversul nu exista daca a si n nu sunt prime intre ele.

[•Andrei1998]

As avea si eu o intrebare. Daca se gaseste cineva binevoitor sa imi raspunda as fi foarte recunoscator:

Daca vrem sa calculam a/b (fractie) mod n, atunci:
a/b = a*inv(b)

In acest topic s-a scris ca inversul nu exista daca b si n nu sunt prime intre ele (intr-adevar 3/4 nu exista mod 7), insa, folosind formula de mai sus, avem ca:
9/3 (mod 6) = 9*inv(3, mod 6) (care, dupa cum s-a zis in topic nu se poate afla caci (3,6)=2)
Dupa logica mea insa, 9/3 (mod 6) = 3 (mod 6) (pe care l-am aflat  )).

Eu, daca l-as avea de aflat pe a/b (mod n) = x (mod n), as face asa:

a (mod n) = b*x+n*y (mod n)
(Impartim toti termenii la (a,b) si rezolvam de aici prin euclid extins (aflam x-ul si y-ul si inmultim iar cu (a,b))). Conditia de existenta a raportului ar fi b|a (nici aici nu sunt prea sigur, corectati-ma).

Mi se pare mult mai dificil de facut chestia asta daca avem a/(b*c). Contraziceti-ma daca gresesc (sau dati-mi o solutie mai simpla decat a mea).

P.S.:Rege nu e Combinari modulare, greseala mea. 

[•alexandru.hulea]

Imi poate explica si mie de ce apare incorect la raspuns pe testele mari? Ca banuiesc ca ultimele 3 teste sunt numerele mari. Am testat si eu pe cateva numere mari si da bine. Cred ca e ceva de conversie, dar nu reusesc sa ma prind ce.

[•AlexandruValeanu]

Salut!
Dupa cum probabil trebuia sa vezi din solutia oficiala( http://www.infoarena.ro/job_detail/227473?action=view-source ) in functia phi daca N este diferit de 1 ( asa NU insemnand ca e prim neaparat ) afisezi

Cod:

if ( B != 1) return ( p/B * ( B - 1 ) );

nu N-1. Cu aceasta modificare sursa ia 100p.

PS: nu mai calcula in conditia de la while sqrt(B); ori calculezi sqrt(B) inainte de while ori pui i*i<=B ca in sursa oficiala.

[•alexandru.hulea]

Multumesc, de-abia acum cand ai zis m-am prins si eu ca B poate scadea sub i*i si totusi sa nu ajunga la 1 , pentru B un numar neprim.

[•manutruta]

Salut!

Imi spuneti va rog ce am gresit ? Am folosit smenul cu ridicare la putere in timp logaritmic, pentru ca nu stiu prea bine euclid extins.

Sursa mea:
http://www.infoarena.ro/job_detail/1095424

Multumesc anticipat,
Manu.

[•mathboy]

In enunt zice ca pentru 60% din teste N este prim, deci daca ai folosit doar ridicarea la putere in timp logaritmic nu ai gresit nimic. Spor la invatat metoda cand N nu este prim.

[•manutruta]

Nu stiam ca functioneaza numai cand N e prim. Se poate fara Euclid extins cand N nu e prim ? Sau trebuie 'musai' sa invat si Euclid extins ?
Daca se poate fara Euclid extins, imi dati va rog un link de unde sa il invat ?

Multumesc anticipat.
Manu.

[•mirceadino]

Al doilea paragraf de la indicatiile de rezolvare te-ar putea ajuta.
Pentru calculul lui 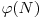(indicatorul lui Euler), vezi aici.

[•dutzul]

Am vazut ca in sursa de la explicatii la algoritmul lui euclid se foloeste operatorul % pe numere negative , is si eu curios cum merge.

[•NicuCJ]

Am o intrebare, folosesc invers modular ca sa calculez Aranjamente(N, K) % 666013. Factorialul imi da la un anumit moment % 666013 valoarea 0, si deci Factorial[N]*invmod(Factorial[N-K]) va da 0. Dar daca as avea, sa zicem A(666015, 1) % 666013, raspunsul ar fi 2. Poate cineva sa imi explice va rog de ce? Multumesc anticipat.

[•PlayLikeNeverB4]

Da 0 pe parcurs doar daca N >= MOD. In acest caz poti aplica http://en.wikipedia.org/wiki/Lucas%27_theorem.

[•k_ounu_eddy]

Nu mi-e foarte clar cum calculam phi.
Cu formula aceasta?(vezi atasament)
Nu prea seamana cu ce face sursa oficiala...
Multumesc

[•AlexandruValeanu]

Este fix formula aia. Doar ca nu inmulteste cu (1 - 1/p) ci cu (p - 1)/p ceea ce este fix acelasi lucru.

[•lucametehau]

In functia din solutia oficiala apare ca parametru &x.
Ce inseamna?