Scurta descriere a unei solutii O(N logN) la problemele Nave
In sursa aceasta am rezumat felul in care arata reteaua de flux pe care o descrie, de fapt, problema. Imaginea se afla intre liniile 164 si 173. Faptul ca o retea de flux maxim de cost minim modeleaza cerinta inseamna ca indeplinim conditiile de convexitate cerute de cele ce urmeaza:
--- Indiciul 1
Se poate folosi tehnica parametric search, zisa si smenul de la Aliens, folosita si la problema Popcorn, problema Sau si la multe altele. Ce poate semnifica lambda pentru problema care ne ramane de rezolvat?
---
Prin urmare, cautam binar cel mai mare lambda pentru care numarul minim (notat cu cnt) de unitati de flux trimise direct la Destinatie, intr-o solutie de cost minim, este mai mic sau egal cu acel numar K dat. Problema se poate rezolva intr-un mod asemanator si daca am vrea sa-l maximizam pe cnt si sa facem cautarea binara putin pe dos, si puteti studia diferentele intre cele doua surse.
--- Indiciul 2
Pe reteaua de flux maxim de cost minim (Gasiti-o!) care modeleaza problema, dandu-se si parametrul lambda, vom gasi costul minim de a trimite toate unitatile de flux de la sursa la destinatie, cu conditia ca orice unitate de flux care ar creste costul cu mai mult de lambda, poate fi "cumparata" cu costul lambda in schimb. Cum putem rezolva in timp liniar aceasta problema?
---
Vom folosi programare dinamica si vom avea grija sa obtinem, in caz de egalitate dupa cost, numarul minim de unitati de flux.
--- Indiciul 3
Fie cost[i][j] = costul minim pe prefixul i daca vin j unitati de flux de la i+1 catre i.
Nota: Definit pentru j >= -(suma de input[p <= i]).
Raspunsul este cost[input.size()-1][ 0 ].
Initializare: cost[-1][j >= 0] = j * lambda, semnificand ca vom cumpara j unitati de flux
Cum se poate scrie recurenta, in asa fel incat sa o implementam in timp liniar in final?
--- Indiciul 4
De la cost[i] la cost[i+1], denumind linia curenta cu dp[], tranzitiile se pot scrie asa:
- dp[j] += |j|: sunt |j| unitati de flux pe muchia i - i+1
- dp'[j] = min(dp[j], dp[j - 1]): trimite 1 unitate de flux de la i+1 la Destinatie
- dp'[j] = min{non-negative p}(dp[j - p] + p * lambda): cumpara p unitati
- dp'[j] = dp[j + input[i + 1]]: sunt input[i + 1] unitati de flux venind dinspre Sursa
Gasiti o metoda de a implementa aceste operatii in timp O(1) amortizat.
--- Indiciul 5
In urma fiecarui set de cate 4 operatii, putem desena in plan valorile din dp[] sub forma unui grafic cu puncte (j, dp[j]). Acest grafic are forma unui sir de segmente cu pante crescatoare, primul segment avand panta negativa, iar ultimul segment avand panta egala cu lambda. E suficient sa retinem, intr-o structura de date, capetele de imbinare ale segmentelor, respectiv cu cat se schimba panta la fiecare imbinare. Desigur, pentru a calcula raspunsul, care este o pereche <cost_total, cnt_operatii_de_tip_2>, vom avea nevoie sa retinem si cateva informatii legate de:
- cate operatii de tipul 2 au fost facute pentru determinarea valorii lui dp0
- care este prima valoare din dp
- care este valoarea primei derivate
Cum se modifica structura aceasta (de preferat sa ganditi pe grafic) la fiecare tip de operatie si cum putem manipula operatiile cat mai eficient? Cum ne putem asigura ca minimizam (sau maximizam) valoarea lui cnt?
---
In imaginea de mai sus puteti vedea cum se schimba graficul in timpul operatiei de tip 1. Practic, segmentul care intersecteaza pozitia 0 este sectionat, intrucat trebuie sa notam ca acolo este o dubla schimbare de panta.
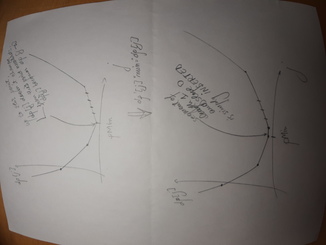
In aceasta imagine puteti vedea cum se schimba graficul in timpul operatiei de tip 2. Tot ce se intampla e ca in dreptul minimului este inserat un segment de lungime 1 si panta 0, partea din dreapta a graficului "mutandu-se" cu o pozitie mai la dreapta, iar cea din stanga ramanand intacta. De asemenea, de retinut ca toate valorile din dreapta minimului nu doar ca si-au schimbat, prin aceasta operatie, valoarea din dp[], ci chiar si acea valoare cnt (care ne spune cate unitati de flux merg direct la Destinatie) este incrementata!
Operatia de tip 3 inseamna sa scadem panta ultimului segment, iar operatia 4 este o simpla shiftare a graficului cu input[i+1] pozitii pe Ox.
--- Indiciul 6
Dat fiind ca ne trebuie operatii de genul:
- shifteaza graficul
- gaseste (1) minimul din dp (echivalent, locul in care panta este 0)
- insereaza in dreptul minimului un segment
- gaseste (2) pozitia indicelui 0 in dp
- modifica pantele in dreptul lui 0
- scade panta ultimului segment (ca din lambda+1 (asa cum a schimbat-o operatia 1) sa redevina lambda)
Cel mai elegant fel de a le realiza este sa tinem o lista dublu inlantuita cu segmentele, care nu vor retine coordonatele lor precise, pentru ca sunt foarte dinamice, ci doar cu cat se schimba panta in dreptul lor si care este lungimea lor. De asemenea, vom retine daca au fost create intr-o operatie de tipul 2 ori ba, intrucat, asta inseamna ca toate segmentele din dreapta lor au trecut prin aceasta operatie iar cnt-ul lor creste cu 1 (sub forma unui smen al lui Mars).
Avem nevoie de iteratorii (1) si (2) pentru a realiza operatiile in timp constant amortizat. Ei trebuie sa retina care este pozitia pe care o indica in sirul dp[], iar iteratorul (1) mai trebuie sa cunoasca si care este panta sa, intrucat informatiile care vin de la segmente (nodurile din lista) sunt de forma "cu cat se schimba panta", doar ca el trebuie sa cunoasca si sa restabileasca o panta in sine. Cum se demonstreaza ca algoritmul este liniar, si cum, mai exact, ne asiguram ca maximizam sau ca minimizam valoarea lui cnt?
---
Bucla critica (cea care da complexitatea) este data de numarul de pasi pe care ii fac ce doi iteratori. In primul rand, vedem ca: operatia 1 schimba panta, adica afecteaza pozitionarea iteratorului (2); operatia 2 poate schimba pozitiile celor doi iteratori cu cate 1 - intuitiv, nu e tocmai ingrijorator; operatia 3 nu ii afecteaza deloc pe iteratori; operatia 4 schimba pozitia iteratorului (2) cu input[i+1]. Deoarece aceasta se intampla intr-un singur sens, si fiecare segment intalnit are lungime cel putin 1, e clar ca plimbarea lui (1) va consta in schimbarea de O(N) ori a nodului catre care indica.
Intrucat nu putem comprima cu usurinta segmente consecutive care pastreaza panta, pentru ca ele retin informatii legate de cnt, la prima vedere, am putea spune ca exista teste pe care comportamentul sa fie patratic: schimbarea pantei, fie ea cu 1 numai, poate influenta pozitionarea iteratorului (2) in asa fel incat sa trebuiasca sa parcurga, dus si intors, de mii de ori, un mare lant de segmente care nu ii schimba panta.
Cheia se afla in faptul ca operatia 1 il atrage practic pe iteratorul (2) inspre (1), oriunde s-ar afla. E clar ca pana ajunge in preajma lui (1), nu poate parcurge mai multe noduri decat cate sunt in total intre cei doi - in total O(N) de-a lungul algoritmului. Dar ce se intampla daca in preajma lui (1) se va "invarti" in jurului lui si ca parcurge adesea mari multimi de segmente egale? Marile multimi acestea nu pot exista, intrucat felul in care se comporta succesiunea operatiilor 1 si 2, ca sa nu mai vorbim si de 4, face in asa fel incat, daca cei doi iteratori sunt aproape unul de altul, segmentele consecutive sa aibe pante diferite.
Cat despre minimizarea (maximizarea) lui cnt, vom face actiona pe doua planuri, pentru a simula corect desfasurarea etapelor din programarea dinamica obisnuita:
- in cadrul operatiei de tip 2, vom insera segmentul cat mai la dreapta (stanga) valorilor minime din sir
- la finalul operatiei de tip 3, vom sterge (ne vom abtine din a sterge) toate segmentele de panta lambda, mai putin pe primul (cel mai la stanga), a carui lungime, o fixam ca fiind infinit
In concluzie, am putea rezuma solutia aceasta ca: smenul de la Aliens + optimizare de dinamica cu slope trick / mentinerea celei de-a doua derivate discrete + liste dublu inlantuite.
