Atenţie! Aceasta este o versiune veche a paginii, scrisă la 2009-01-25 14:49:02.
Revizia anterioară Revizia următoare

Deque şi aplicaţii

(Categoria Structuri de date, Autor Xulescu)

În acest articol voi prezenta o structură de date de tip listă numită deque şi o serie de aplicaţii utile care vă vor demonstra simplitatea şi utilitatea folosirii acesteia, în special în concursurile de informatică.

Introducere

Dequeul (pronunţat de obicei deck) poate fi privit ca o colecţie de tip listă ce are două capete prin care se şterg sau inserează noi elemente. În literatura de specialitate, aceste capete se numesc head şi tail, iar dequeul mai este recunoscut şi ca fiind o coadă cu două capete (double ended queue).

Un deque poate fi implementat folosind liste dublu înlănţuite, sau cu un vector static când se cunoaşte numărul elementelor din colecţie. Ce trebuie reţinut este că limbajul C++ pune la dispoziţia utilizatorilor prin intermediul headerului #include <deque> clasa std::deque.

Operaţii

Mai jos sunt operaţii ce se pot efectua cu un deque, iar în stânga corespondentul lor în limbajul C++:

front(): întoarce primul element;
back(): întoarce ultimul element;
push_front(): inserează un element în faţă;
push_back(): inserează un element în spate;
pop_front(): scoate primul element;
pop_back(): scoate ultimul element.

Toate aceste operaţii se execută în timp O(1) amortizat.

Aplicaţii

Unde-i folosit dequeul? :-?

Problema 1: Book Pile (SGU)

Se dau N cărţi aşezate una deasupra celeilalte asupra cărora se vor efecta M operaţii de două tipuri: 1. ADD(nume) : se adaugă cartea nume deasupra celorlalte; 2. ROTATE : primele K cărţi de deasupra se rotesc (dacă sunt mai puţin de K cărţi atunci se vor roti toate). Se cere să se afişeze cărţile în ordine, prima fiind cea de deasupra, după efectuarea celor M operaţii.
Restricţii: 0 ≤ N, K ≤ 40 000, 0 ≤ M ≤ 100 000.

Soluţie:

Soluţia problemei se poate deduce urmând paşii următori. Să presupunem că avem cărţile A B C iniţial şi K = 3. Dacă îl vom adăuga pe D, atunci nu vor rămâne importante decât cărţile D A B, deoarece, dacă vom roti ulterior ultimele K cărţi, C nu va mai fi niciodată considerat, cărţile fiind doar adăugate, iar o dată ce o carte iese din „top K” cărţi nu va mai fi posibil să i se schimbe poziţia pe raft. Să rotim acum „top K” cărţi. Noua ordine va fi B A D şi C pe raft la loc sigur. Dacă îl vom adăuga pe E, topul se va schimba în E B A iar pe raft, în mod sigur vor fi, în această ordine, D C. Proprietatea celor K cărţi din vârf este: o secvenţă continuă de elemente, la care se adaugă noi elemente sau se elimină dintre acestea numai pe la capete. Aceste capete sunt chiar head şi tail ale unui deque.

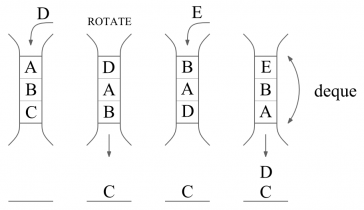
La final, când se vor termina operaţiile, cărţilor de pe raft li se vor adăuga cele din deque şi se va afişa soluţia. În cazul presupus, soluţia va fi: E B A D C.

Întrucât operaţiile unui deque se execută în O(1) amortizat, soluţia are complexitatea O(N + M).

Problema 2: Sir

Se dă un şir S de numere întregi de lungime N. Se cere să se găsească secvenţa de lungime maximă cuprinsă între X şi Y astfel încât MAX - MIN ≤ Z, unde MAX este maximul dintre toate numerele întregi din secvenţă iar MIN minimul dintre acestea. Secvenţa soluţie va fi cea cu poziţia de început maximă dintre toate secvenţele de lungime maximă.
Restricţii: 3 ≤ N ≤ 100 000, 1 ≤ X ≤ Y ≤ N, 0 ≤ Z ≤ 30 000.

Soluţie

Voi prezenta mai jos o rafinare a soluţiei în trei paşi.

Prima rezolvare se găseşte uşor, deoarece nu facem decât să urmărim textul: pentru fiecare poziţie i fixată (i ia valorile 1, 2, .., N succesiv) vom determina pentru aceasta secvenţa cerută, adică vom plimba un j între poziţiile i - Y şi i - X. Pentru un interval (j, i] vom determina MAX şi MIN în O(log₂N) cu un arbore de intervale, iar daca diferenţa dintre acestea nu depăşeşte Z vom compara cu soluţia finală. Complexitatea finală va fi O(N * (Y - X) * log₂Y).

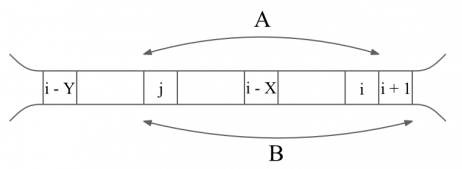
Să presupunem că pentru poziţia curentă i, l-am găsit pe j cuprins între i - Y şi i - X care îndeplineşte optimul. Ce proprietăţi are j?

i - Y ≤ j ≤ i - X şi MAX - MIN ≤ Z;
dacă îl incrementăm pe j la j + 1 atunci dacă j ≤ i - X cu siguranţă MAX - MIN ≤ Z şi astfel soluţia va fi mai scurtă;
dacă îl decrementăm pe j, atunci ori j < i - Y ori MAX - MIN > Z;
dacă îl incrementăm pe i la i + 1, atunci se poate întâmpla ca j < i - Y; cum MAX nu poate decât să crească, iar MIN decât să scadă, se mai poate de asemenea întâmpla ca MAX - MIN > Z.

Datorită proprietăţilor de mai sus, când trecem de la i la i + 1, valoarea lui j nu poate decât să crească cât timp MAX - MIN > Z şi j nu a depăşit poziţia i - X. Pentru determinarea lui MAX, respectiv lui MIN se poate folosi un arbore de intervale. Complexitatea finală va fi O(N * log₂(Y)).

Cu cei doi indici i şi j vom accesa fiecare element din cele N de cel mult 2 ori, o dată cu i şi o dată cu j. Destul de eficient. Să vedem cum putem îmbunătăţi complexitatea O(log₂Y) pentru determinarea maximului şi minimului.

Pentru fixarea ideilor să urmărim cum îl calculăm pe MAX. Observaţia care ne ajută în multe probleme pentru reducerea complexităţii de la O(log₂N) la O(1) amortizat este următoarea: „Fixăm i₁ şi i₂ astfel încât j < i₁ < i₂ ≤ i. Atunci, dacă S[i₂] > S[i₁] poziţia i₂ va fi întotdeauna mai importantă decât poziţia i₁ atâta timp cât cele două poziţii vor fi în intervalul (j, i]. Când i₁ şi i₂ nu vor mai fi în intervalul (j, i], poziţia eliminată va fi i₁”. Rezultă din această observaţie că în intervalul (j, i] poziţiile importante vor fi j < i₁ < i₂ < .. < i_k <= i astfel încât S[i₁] > S[i₂] > .. > S[i_k]. Astfel MAX va fi S[i₁]. Când îl vom incrementa pe i la i + 1 vom şterge din poziţiile i_k, i_k-1, ... atâta timp cât S[i + 1] este mai important, adică mai mare decât valorile de pe aceste poziţii, şi vom şterge i₁, i₂, ... atâta timp cât aceste poziţii sunt mai mici sau egale decât j'. Indicele j' este noul optim pentru poziţia i + 1. Proprietatea şirului de poziţii i₁, i₂, .., i_k este că se reprezintă ca un şir contiguu de numere care permite inserarea elementelor prin dreapta şi ştergerea prin stânga, adică se adaugă elemente la tail şi se şterg elemente de la head. Îl putem deci reprezenta printr-un deque. Complexitatea O(1) amortizat provine de la faptul că fiecare poziţie dintre cele N nu trece decât o singură dată prin deque şi este şters tot cel mult o singură dată.

În practică, programul poate arăta în felul următor:

#include <fstream>
#include <deque>
#include <vector>
#include <algorithm>

using namespace std;

const char iname[] = "sir.in";
const char oname[] = "sir.out";

typedef int (*PF)(const int& , const int& ) ;

deque <int> min_deq, max_deq;

vector <int> V;


int min_fct(const int& a, const int& b) { return a < b; }

int max_fct(const int& a, const int& b) { return a > b; }

void push_in(deque <int>& deq, int& p, PF compare) {
    for (; !deq.empty() && compare(V[p], V[deq.back()]); deq.pop_back()) ;
    deq.push_back(p);
}

int query(deque <int>& deq, const int& first) {
    for (; !deq.empty() && deq.front() <= first; deq.pop_front()) ;
    return V[deq.front()];
}

int main(void)
{
    ifstream in(iname);  ofstream out(oname);
    int N, X, Y, Z;
    int length = 0, start = 0, stop = 0;

    int j = 0;

    in >> N >> X >> Y >> Z;
    V.resize(N + 1);
    for (int i = 1; i <= N; ++ i) {
        in >> V[i];
        // (j, i] este intervalul candidat la solutia pentru pozitia i;
        push_in(min_deq, i, min_fct);
        push_in(max_deq, i, max_fct);

        while ((j < i - Y || query(max_deq, j) - query(min_deq, j) > Z) && j < i - X)
            j ++;

        if (j <= i - X) if (query(max_deq, j) - query(min_deq, j) <= Z)
            if (i - j >= length)
                length = i - j, start = j + 1, stop = i;
    }

    if (length > 0)
        out << length << " " << start << " " << stop << "\n";
    else
        out << -1;

    in.close(), out.close();
    return 0;
}

Complexitatea finală va fi O(N).

Problema 3: Trans (ONI 2004)

(gen bun de problema)
...

Problema 4: Otilia (.campion)

(deque la o problema de teoria jocurilor)
...

Problema 5: Cut the Sequence (PKU)

(deque cu arbori de intervale, zice Paul)
...

Problema 6: Bcrc (Stelele Informaticii 2006)

(deque la programare dinamica)
...

Concluzii

Nicio concluzie până acum.

Probleme suplimentare

Secvenţă
Secvenţă 3
Secvenţă 4
Brânză
Struţi
Trompetă
Buline
Balans
Gard, ONI 2002 (Cred că ar merge mai bine la aplicaţii)
Ghiozdan
Munte4, Lotul Naţional de Informatică, 2005
Cover, Baraj ONI 2007

Bibliografie

Cosmin Negruşeri, Probleme cu secvenţe
Dana Lica, Arbori de intervale şi aplicaţii în geometria computaţională

infoarena informatica de performanta