Solutii Algoritmiada 2019, Runda PreOJI

Solutia problemei Marceland

Numim componenta 4-conexa o multime maximala de celule, pentru care, oricum am alege doua celule din aceasta multime, exista un drum intre acestea mergand doar prin celule care nu contin # (nu sunt blocate) si trecand dintr-o celula doar intr-o alta celula care are o latura comuna cu ea.
Problema se reduce la determinarea tuturor componentelor 4-conexe si adaugarea convenabila a fantanilor: pentru o componenta care contine cel putin un Marcel, dar nu contine nicio fantana, se cauta o celula cu nisip din aceasta componenta si se inlocuieste cu o fantana, daca nu exista o celula cu nisip disponibila (componenta conexa contine doar M) atunci nu avem solutie.

In functie de metoda de determinare a componentelor 4-conexe se pot obtine punctaje diferite:

  • Pentru N=1, componentele conexe sunt determinate de intervale compacte maximale care nu contin #. Putem astfel determina componentele conexe printr-o simpla parcurgere a vectorului, numarand fiecare tip de celula intalnita in componenta curenta.
  • Pentru N=2, consideram mai intai intervalele compacte maximale de pe cele doua linii care nu contin # (asemanator cu situatia anterioara). Pentru a determina componentele conexe, sortam aceste intervale dupa capatul stanga, apoi le parcurgem in aceasta ordine mentinand care este cel mai mare capat dreapta al unui interval deja procesat. Componentele conexe sunt gasite de la stanga la dreapta astfel: daca acest capat dreapta maxim este cel putin egal cu capatul stanga al intervalului curent, atunci intervalul curent apartine ultimei componente conexe determinate si actualizam informatiile pentru aceasta componenta, altfel incepe o componenta noua, iar pentru componenta anterioara detinem deja informatiile finale.
  • Pe cazul general, putem aplica o parcurgere in latime (BFS) din celule care contin M, astfel: cautam o celula care contine M si nu a fost vizitate, folosind parcurgerea in latime marcam ca vizitate toate celulele la care are acces acest M (determinam astfel componenta sa 4-conexa) si numaram cate celule de tip fantana sau nisip am gasit, putand astfel da un raspuns pentru componenta curenta; cat timp mai exista celule M nevizitate reluam procesul. Complexitate timp: O(N*M).

Solutia problemei Panza

Solutia pleaca de la construirea unui tablou bidimensional d, in care d[i][j] are semnificatia urmatoare: lungimea minima a unui drum care pleaca din punctul S de pe primul segment, ajunge pe segmentul i in punctul j si trece prin fiecare interval cu vitamine pentru toate segmentele de la 1 la i. Astfel putem simula constructia unui drum de lungime cat mai mica. Pentru initializare, d[ 1 ][i] = |i - S|, pentru calcul efectiv, vom folosi recurenta ce urmeaza sa fie descrisa, iar pentru raspunsul final vom fi interesati in valoarea minima ce poate fi obtinuta alegand convenabil o valoare pos si gasind solutia d[N][pos] + |pos - F|.

Pentru recurenta, presupunand ca am calculat d[i - 1][p], pentru oricare p intre X[i - 1] si Y[i - 1], vom dori sa calculam d[i][j], pentru oricare j intre X[i] si Y[i]. Trebuie sa fim atenti, deci, sa nu consideram drumuri care nu iau vitamina i sau i - 1.

Relevant pentru recurenta este pozitia p a carei valoare d[i - 1][p] o consider, cat si pozitia q unde folosesc puntea de lungime A[q]. In functie de acestea, putem scrie ca:

d[i][j] = minim {d[i - 1][p] + |p - q| + A[q] + |q - j|}, considerand orice q de la 1 la M si orice p de la X[i - 1] la Y[i - 1].

In functie de cat de eficient este realizata aceasta decizie de minim, se pot obtine solutii de mai multe complexitati ca timp:

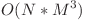O(N * M^3) - 30 de puncte

Se fixeaza p si q si se alege, dupa recurenta descrisa, solutia cea mai buna.

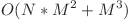O(N * M^2 + M^3) - 70 de puncte

Se observa ca daca il fixam pe p, aflarea celui mai bun q, adica minimizarea lui |p - q| + A[q] + |q - j|, nu tine cont de i, deci putem precalcula tabloul r[j][p] cu semnificatia: care e cea mai mica valoare |p - q| + A[q] + |q - j|, alegandu-l convenabil pe q.

Astfel, precalcularea are complexitatea 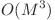O(M^3) pentru ca pentru ca fiecare j si p incercam toate pozitiile q.

De asemenea, recurenta devine:

d[i][j] = minim {d[i - 1][p] + r[j][p]}

Prin urmare, la fiecare i si j, iteram doar prin Y[i - 1] - X[i - 1] + 1 optiuni de valori ale lui p, adaugand la complexitate 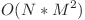O(N * M^2)

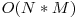O(N * M) - 100 de puncte

Vom face cateva calcule intermediare de complexitate 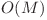O(M) pentru fiecare segment, astfel:

Mai intai calculam x[j] care e costul minim sa ajung in punctul j pe segmentul i - 1, stiind ca prin punctul j trec, pe punctea de lungime A[j], pe segmentul i. Pentru inceput, x[j] = d[i - 1][j], daca X[i - 1] ≤ j ≤ Y[i - 1], sau infinit daca nu. Apoi facem o parcurgere de la 2 la M si zicem x[j] = min {x[j], x[j - 1] + 1}. Apoi facem o parcurgere de la M - 1 la 1 si recalculam x[j] = min {x[j], x[j + 1] + 1}. Astfel, simulam o plimbare pe segmentul i - 1.

Apoi calculam y[j] = x[j] + Aj, adica am trecut prin puntea j pe segmentul i. Apoi facem o parcurgere de la 2 la M si zicem y[j] = min {y[j], y[j - 1] + 1}. Apoi facem o parcurgere de la M - 1 la 1 si recalculam y[j] = min {y[j], y[j + 1] + 1}. Astfel, simulam o plimbare pe segmentul i.

Acum, nu ne mai ramane de facut decat sa notam ca d[i][j] = y[j] daca X[i] ≤ j ≤ Y[i], sau infinit daca nu.

De observat ca aceste calcule pot fi facute cu un singur sir d[1...M], nefiind nevoie nici de tabloul bidimensional d, nici de x sau y.

Observatie: Solutia nu se foloseste de faptul ca Ai ≤ Ai+1. Acest detaliu este unul care sa simplifice vizualizarea panzei de paianjen

Solutia problemei Tablou

Concurentul theodor.moroianuTheodor Moroianu •theodor.moroianu s-a oferit sa descrie solutia sa la aceasta problema:

Subtask 1:

Salvam intr-o matrice tridimensionala tablourile fiecarei fete:

Mat[id][i][j] este culoarea de pe pozitia (i, j) din tabloul fetei id.

In 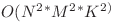O(N^2^ * M^2^ * K^2^) calculam diferenta ceruta.

Subtaskurile 2,3:

Majoritatea solutiilor din subtaskurile acestea sunt:

  1. Optimizari ale solutiei din Subtaskul 1
  1. Solutii bazate pe frecventa cifrelor 0...9
  1. Solutii ne-optimizate din Subtaskul 4 bazate pe observatia prezentata tot acolo

Subtask 4:

Exista diferite solutii care sa ia 100 de puncte, complexitatea cea mai putin eficienta care sa intre in timp fiind

O(N*M*10 + 100*Q)

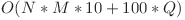
O sa analizam mai departe o solutie cu complexitatea 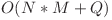O(N*M+Q)

Observatia de baza pentru aceasta solutie este ca suma \sum_{B,a,b,p,q}^{} A[a][b]-B[p][q] poate fi scrisa sub forma N*M*(\sum_{a,b}^{} A[a][b]-\sum_{p,q}^{} B[p][q])

Raspunsul pentru o anumita poza poate deci fi scris sub forma \sum_{poza B!=a}^{} {N*M*(\sum_{a,b}^{} A[a][b]-\sum_{p,q}^{} B[p][q])}

= N*M*Q* \sum_{a,b}^{}{A[a][b]}-N*M*\sum_{poza B!=a}^{} {(\sum_{p,q}^{} B[p][q])}

Astfel, pozitiile / frecventele valorilor din imagini nu ne mai intereseaza, vrem doar sa stim suma lor!

Fie 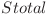Stotal suma tuturor elementelor tuturor pozelor, si s[i] suma elementelor din poza i.

Raspunsul pentru o poza k o sa fie N*M*(Q*s[i] - (Stotal-s[i])).

Solutie alternativa

Aceasta este solutia autorului.

Vom nota cu S = 10 numarul de cifre in baza 10, altfel spus marimea alfabetului cu care sunt descrise tablourile, pentru conturarea complexitatilor solutiilor ce urmeaza:

Pentru 10 puncte

Solutia de complexitate 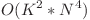O(K^2 * N^4) timp si 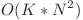O(K * N^2) memorie nu face decat sa creeze cele K tablouri si sa calculeze conform enuntului costul fiecaruia. Se fixeaza tabloul caruia vrem sa ii calculam costul, de unde un factor de 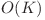O(K) , se fixeaza tabloul cu care il comparam, alt 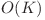O(K) , se fixeaza pozitia (a, b) in 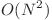O(N^2) si pozitia (p, q) in 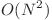O(N^2) , si se adauga la raspuns diferenta intre cele 2 caractere.

Pentru 30 - 50 de puncte

Prima observatie ce poate fi facuta e ca putem scurta mult calculul dereglarii a doua tablouri daca, in loc sa consideram toate pozitiile cu toate poitiile, le grupam in functie de cifra lor. Cu alte cuvinte, e suficient sa cunoastem sirul fr[t][0...9] care ne spune, pentru tabloul t, cate cifre de 0, de 1, ..., de 9 are in el.

Astfel, putem calcula, parcurgand fiecare tablou, acest sir fr[t][0...9]. Cand vrem sa calculam dereglarea dintre tablouri, e suficient sa fixam cifra c1 din primul tablou t1 si cifra c2 din al doilea tablou t2 si sa adunam la valoarea primului tablou fr[t1][c1] * fr[t2][c2] * (c1 - c2). Complexitatea este 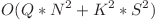O(Q * N^2 + K^2 * S^2) timp si 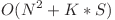O(N^2 + K * S) memorie.

Pentru 60 de puncte

O alta observatie ce poate fi facuta este ca nu trebuie sa obtinem explicit fiecare tablou pentru a calcula sirul sau fr[0...9]. Este suficient sa stim sirul asociat tabloului initial al lui Marcel si cate cifre de 0, de 1, ..., respectiv de 9 se afla in submatricea unde se recoloreaza cu culoarea cul. Pentru a cunoaste aceasta, e suficient sa precalculam un tablou de sume partiale pentru fiecare cifra in parte, astfel:

S[ c ][i][j] = numarul de cifre c din submatricea cu coltul stanga-sus in celula (1, 1) si coltul dreapta-jos in celula (i, j).
S[ c ][i][j] = S[ c ][i - 1][j] + S[ c ][i][j - 1] - S[ c ][i - 1][j - 1] + (1 daca T[i][j] = c, 0 daca nu)
Calculul acestui tablou tridimensional are complexitate 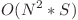O(N^2 * S) atat ca timp, cat si ca memorie.

Atunci cand vrem sa calculam sirul fr[0...9] al unui anumit tablou, putem copia frecventa cifrelor din cel initial, apoi putem scadea din fr[ c ] numarul de cifre egale cu c din submatricea recolorata, adica S[ c ][lin2][col2] - S[ c ][lin2][col1 - 1] - S[ c ][lin1 - 1][col2] + S[ c ][lin1 - 1][col1 - 1]. La final, adaugam (lin2 - lin1 + 1) * (col2 - col1 + 1) la fr[cul].

Complexitatea solutiei este 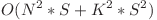O(N^2 * S + K^2 * S^2) timp si 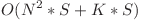O(N^2 * S + K * S) memorie, intrucat pentru calculul valorii fiecarui tablou vom proceda asemanator cu solutia precedenta.

Pentru 100 de puncte

Observatia finala se bazeaza pe faptul ca dereglarea dintre doua tablouri t1 si t2 este egala cu deregalarea dintre t1 si tabloul lui Marcel minus dereglarea dintre t2 si tabloul lui Marcel. (Vectorial, am putea spune ca 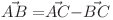$$\vec{AB} = $$\vec{AC} - $$\vec{BC} ).

Astfel, putem calcula in 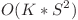O(K * S^2) dereglarea dintre fiecare tablou si tabloul lui Marcel, pe care o notam cu V[t]. Fie sum suma tuturor acestor dereglari V[t]. Atunci valoarea unui tablou este egala cu V[t] * K - sum.

Complexitate finala: 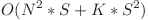O(N^2 * S + K * S^2) timp si 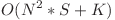O(N^2 * S + K) memorie.