Solutii Algoritmiada 2014 Runda 2
Memcpy
Fiecare celula (x,y) din submatricea noua va avea coresponentul (x + DX, y + DY) in submatricea veche, unde (DX, DY) e pozitia relativa a celor doua submatrice.
Trebuie sa avem grija sa nu suprascriem elementele din submatricea veche pe care inca nu le-am copiat la pozitia lor finala.
Memoram intr-o structura de date S toate celulele a caror informatie a fost copiata deja.
Initial acestea reprezinta celulele din noua submatrice care nu fac parte din vechea submatrice. (nu avem nevoie de acele informatii)
La fiecare pas trebuie sa extragem o celula (x, y) din S si copiem informatia din (x + DX, y + DY) in (x, y), dupa care introducem celula (x + DX, y + DY) in S.
Pentru a asigura si copierea in ordine minima din punct de vedere lexicografic extragem tot timpul celula minima lexicografic.
Aceasta se poate face (printre altele) cu un set.
Complexitatea acestei solutii este O(N*M*log(N*M)).
Semne3
Avem de completat N pozitii cu numere de la 1 la N. Pentru ca solutia sa fie minima din punct de vedere lexicografic, trebuie ca pe fiecare pozitie sa punem un numar cat mai mic care sa ne permita sa completam si restul pozitiilor.
Fie sirul ">". Avem de completat doua pozitii. Am dori sa punem pe prima pozitie 1, insa aceasta nu ne-ar permite sa punem o valoare valida pe a doua pozitie.
Fie sirul ">>". Pe prima pozitie vom pune un numar x dupa care vor urma inca doua numere care trebuie sa fie obligatoriu mai mici ca x. Cel mai mic x valid este x=3.
De aici rezulta un algoritm greedy care proceseaza subsecventele "<<...<<" si ">>...>>" de le stanga la dreapta.
Vom tine o lista cu toate numerele disponibile. Initial aceasta contine toate numerele de la 1 la N.
Luam toate subsecventele la rand. Pentru fiecare dintre acestea, vom completa numarul de dinaintea fiecarui semn.
Pentru fiecare subsecventa avem doua cazuri. Notam lungimea subsecventei cu K.
Cazul "<<...<<": Completam pozitiile cu cele mai mici K numere in ordinea din lista.
Cazul ">>...>>": Fie cele mai mici K numere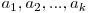 
. Deoarece dupa cele K pozitii va urma inca un numar care e mai mic decat restul, trebuie sa lasam disponibil un numar. Deci completam pe aceste pozitii, in aceasta ordine, 
.
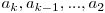Pe ultima pozitie (dupa ultimul semn) punem singurul numar ramas disponibil.
Complexitatea acestei solutii este O(N).
Collar
Prima observatie pe care trebuie sa o facem este ca lungimea subsecventelor in care impartim sirul trebuie sa fie un divizor al lungimii sirului initial.
In continuare, vom incerca sa rezolvam problema presupunand ca subsecventele au o lungime fixata K. Pentru a rezolva circularitatea sirului, il vom concatena la el insusi. Astfel, avem un sir de lungime 2 * N in care vrem sa gasim o subsecventa de lungime N care incepe pe pozitia i si se termina pe pozitia i + N - 1, iar suma Max{V[j], j = i...i + K - 1} - Min{V[j], j = i...i + K - 1} + Max{V[j], j = i + K...i + 2 * K - 1} - Min{V[j], j = i + K...i + 2 * K - 1} + ... sa fie maxima. Aceste maxime/minime pot fi calculate pentru fiecare subsecventa de lungime K cu ajutorul unui deque, apoi nu ramane decat sa tinem sume partiale de tipul Sum[i] = Max[i - K + 1...i] - Min[i - K + 1...i] + Sum[i - K]. Pentru fiecare subsecventa de lungime N, vom actualiza raspunsul cu Sum[i] - Sum[i - N].
Astfel, complexitatea de timp este O(N).
Deoarece numarul divizorilor este cel mult sqrt(N), putem verifica fiecare lungime posibila.
Complexitatea totala este O(N * sqrt(N)).
Plagiat
Problema se rezolva pe baza unei observatii simple . Atunci cand un triunghi se poate obtine din celalalt printr-o translatie inseamna ca cele doua triunghiuri sunt la fel , astfel doar pozitia lor in plan e diferita. Asadar , fiecare varf impreuna cu un varf de la celalalt triunghi formeaza un segment . Aceste trei segmente trebuie sa aibe aceeasi lungime si aceeasi panta. Solutia aceasta poate fi calculata usor cu un hash sau map din STL , avand complexitatea O(N^2 * hash ) .
Ninja
Solutie O(M * K) - 30 de puncte
Aceasta solutie este ineficienta, dar reprezinta un punct de plecare pentru solutia optima. Reprezentam gramezile de aur ca si o pereche (C, LEN),
unde C este centrul gramezii iar LEN este lungimea acesteia.
De exemplu, putem reprezinta grafic o gramada de lungime 5 astfel: 12321, unde fiecare cifra reprezinta indicele (si inaltimea) lingoului.
Fie intervalul din query [A,B].
Observam ca pentru ca un lingou sa fie nesupravegheat trebuie ca intervalul sa acopere ambele pozitii la care apare indicele lui. Deci, putem deduce o regula pentru a afla numarul de lingouri nesupravegheate.
Daca gramada e inclusa complet in interval atunci toate lingourile din gramada sunt nesupravegheate. In caz contrar, calculam distanta minima a centrului fata de A si B. Fie D = min(C-A+1, B-C+1). Se poate observa ca doar D lingouri raman nesupravegheate.
Deci, pentru fiecare query insumam raspunsul de pe fiecare rand.
Solutie O(MlogM + KlogK + KlogN + MlogN) - 100 de puncte
Putem imparti fiecare query [A,B] in doua query-uri [A,X] si [X+1,B], unde X = (A+B)/2. Acest lucru ne ajuta la determinarea usoara a raspunsului pentru fiecare gramada.
Ne concentram asupra partilor stangi ale query-urilor, celelalte tratandu-se similar. Fie un query [A,X] si o gramada un centrul C si limita stanga L.
Daca C se afla in afara intervalului atunci aceasta gramada nu contribuie cu nimic la acest query.
Daca C e inclus in [A,X] atunci avem doua cazuri:
1) L e inclus in [A,X]. In acest caz gramada e complet inclusa in [A,B], deci raspunsul e C-L+1.
2) L < A. Stim ca D = min(C-A+1, B-C+1). In acest caz C-A+1 <= B-C+1, deci D = C-A+1.
Cu alte cuvinte, pentru fiecare celula din [L,C] inclusa in [A,X] adaugam 1 la rezultat.
Vom precesa query-urile offline. Sortam gramezile dupa centru si query-urile dupa capatul drept. Vom tine un arbore de intervale pentru suma pe coloane.
Parcurgem coloanele de la 1 la M. Fie coloana curenta i. Pentru fiecare centru C = i updatam arborele adaugand 1 pe intervalul [L,C]. Raspunsul pentru acest query [A,i] va fi suma de pe intervalul [A,i].
