Solutii Algoritmiada 2014 Runda 1

Permut

Observam ca pentru a obtine o suma de produse maxima avem nevoie sa inmultim cele mai mari numere intre ele si la fel cu cele mai mici.
In cazul numerelor negative se pastreaza regula. Cu alte cuvinte sortam cele 2 siruri si inmultim numerele in ordinea lor, doua cate doua
O demonstratie mai riguroasa a algoritmului se poate face prin reducere la absurd.

3color

Sa uitam pentru un moment de constantele aruncate de problema pentru a ne incurca.
Vrem sa coloram un graf in numar cat mai mic de culori astfel incat oricare 2 noduri conectate printr-o muchie au culori distincte.
Un posibil brut ar fi ca mai intai sa gasim o colorare pentru graful format din primele n - 1 noduri si sa alegem culoarea nodului ramas drept cea mai mica culoare nefolosita de vecinii sai. Acest "brut" care poate parea ineficient ne garanteaza o colorare in maxim 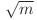\sqrt{m} culori. O demonstratia a acestui lucru revine din faptul ca un nod de culoare k ar trebui sa aibe muchii catre noduri cu culorile 0, 1 ... k-1, astfel existenta unui nod de culoare k implica existenta a k muchii si a unor noduri de culorile 0, 1, ... k - 1 care implica mai departe existenta a unui total de 0 + 1 + ... + k = \frac{k * (k + 1)}{2} muchii. Insa acesta este doar un worstcase, putem imbunatati performanta algoritmului prin procesarea nodurilor in ordinea inversa a numarului de muchii sau chiar prin randomizarea ordinii de procesare.

Chiar daca teoretic am obtine in worstcase o partitionare cu 123 de culori algoritmul este avantajat si de structura specifica a grafului (3-colorabil) si astfel obtine o partitionare cu sub 100 de culori.

Magicmatrix

Sa presupunem ca avem suma S = A1P1 + ... + AiPi + ... + AjPj + ... + ANPN. Daca schimbam Pi cu Pj (facem o transpozitie in permutare) inseamna ca vom obtine S = A1P1 + ... + AiPj + ... + AjPi + ... + ANPN, de unde deducem ca AiPi + AjPj = AiPj + AjPi, oricare ar fi Pi si Pj. Cu alte cuvinte, orice dreptunghi trebuie sa aiba suma colturilor opuse egala. Aceasta este o conditie necesara, dar si suficienta ca o matrice sa fie “magica”.
De aici deducem o solutie imediata cu complexitate O(N4), in care verificam toate dreptunghiurile posibile.
Pentru a obtine 100 de puncte exista mai multe variante. Toate se bazeaza pe aceeasi idee: nu e nevoie sa verificam fiecare dreptunghi in parte. Este suficient, de exemplu, sa verificam doar pentru patratele 2×2 din matrice, intrucat din relatiile care se obtin pentru toate patratele 2×2 se pot deduce relatiile pentru toate celelalte dreptunghiuri. Astfel se obtine o complexitate de O(N2).

Mission

Problema cere, de fapt, un poligon (nu neaparat convex) care nu se auto-intersecteaza si care are ca varfuri cele N puncte date.
Solutia oficiala se bazeaza pe un algoritm constructiv. Mai intai, determinam infasuratoarea convexa a punctelor. Daca parcurgem punctele incepand cu cel mai mic x pana la cel mai mare x (fie cele de pe “lower envelope”, fie cele de pe “upper envelope”), iar apoi sortam punctele ramase descrescator dupa x si le parcurgem in aceasta ordine, vom obtine un poligon care nu se auto-intersecteaza.

O alta solutie care obtine 100 de puncte, dar nu este la fel de usor de demonstrat este urmatoarea: se calculeaza punctul care are ca si coordonate media aritmetica a coordonatelor celor N puncte, iar apoi le sortam in functie de panta pe care o formeaza cu acest punct. Aceasta ordine va determina un poligon care nu se auto-intersecteaza.
Atentie! Trebuie neaparat ales un punct din interiorul infasuratorii convexe. In caz contrar, pot aparea probleme atunci cand se inchide poligonul, in special daca sunt cadrane fara niciun punct.

Ambele solutii au complexitate O(N * logN).

Kami

Vom presupune urmatoarele notatii:
- N - numarul de nr
- A[] - sirul de numere
- sum[i][j] (i <= j) - A[i] + A[i + 1] + ... + A[j]
- S[i] = A[i] + A[i + 1] + ... + A[n]
- B[i] = A[i] - S[i + 1]
Observam ca sum[i][j] = S[i] - S[j + 1] (1)

Pentru un query de tip 1, avand pozitia de start j vrem sa gasim i < j maxim a.i. A[i] - sum[i + 1][j] >= 0. Din observatia 1, inegalitatea dinainte se rescrie: A[i] - S[i + 1] + S[j + 1] >= 0 <=> A[i] - S[i + 1] >= -S[j + 1], care se rescrie in final ca B[i] >= -S[j + 1]. Astfel, problema acum cere gasirea unui i < j maxim a.i. B[i] >= o val data (problema mai usoara). Exista 2 abordari, fiecare obtinand punctajul maxim in continuare:

Solutia 1:

Mentinem un arbore de intervale ce contine maximul in fiecare nod pt valorile B[] si inca un arbore de intervale cu suma in fiecare nod(sau un aib) pt valorile A[]. Astfel cand avem un query 1 j, aflam S[j + 1] in O(log N) si ulterior pozitia i cautata in O(log N). In cazul unei operatii de tip 0 (update), vom face un lazy update pe primul arbore de intervale (continand valorile B) si un update normal pe cel de-al doilea.
Complexitate finala: O((N + M) log N).

Solutia 2:

Abordam o strategie asemanatoare cu solutia 1, cu exceptia faptului ca nu vom mai folosi un arbore de intervale pt valorile B[], ci vom mentine maximul pe bucati de lungime sqrt N. Astfel, operatiile de query si update se vor efectua fiecare in complexitate O(sqrt N). Desi aceasta solutie este dpdv teoretic mai inceata, are avantajul de a fi mult mai scurta, putand fi implementata usor in timpul unui concurs.
Complexitate finala: O(N + M * sqrt N).

Sistem3