Solutii Algoritmiada 2013, Runda Finala

• Lista de probleme
• Noname
• Permsplit
• Return of the MVC
• Parb
• Mai marii orasului
• Timetravel

Noname

Solutia este unica.
Vom prezenta mai intai algoritmul greedy de rezolvare a acestei probleme si apoi vom putea demonstra de ce este unica.

• Pasul 0 : Pentru inceput marcam fiecare element (i,j) ca fiind nedecidabil.
• Pasul 1 : Primele elemente cu care putem spune cu certitudine ca au o anumita valoare sunt elementele de pe coloanele si liniile ce corespund elementului N din cele doua permutari.
• Pasul 2 : Dupa ce am umplut liniile de 1 am aflat pozitii pentru care avem certitudinea ca au valoarea 1 si pentru alte linii si coloane. Dintre toate acestea avem certitudinea ca aceasta este singura pozitie de 1 de pe liniile si coloanele corespunzatoare valori 1 din cele doua permutari. In acest mod putem spune clar ca toate celelalte elemente ale acestor linii si coloane au valoarea 0.
• Pasul 3 : Acum cunoastem pozitia singurei valori de 0 pentru liniile si coloanele corespunzatoare valorilor N-1 din cele doua permuatari si le putem marca in consecinta.
• Pasul 4 : Acum cunoastem pozitia celor 2 elemente ce au valoarea 1 in liniile si coaloanele corespunzatoare valorii 2 din cele doua permutari si putem atribui celorlalte elemente ca au valoarea 0.
• ... Pasul N : Vom umple dupa aceeasi deducere urmatoarele linii si coloane dupa care avem informatii suficiente pana la ultimul element caruia ii mai trebuie asociata doar pozitia (N/2,N/2)

Complexitatea finala a algoritmului este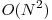
Deoarece fiecare pas al algoritmului ne duce intr-o unica solutie, oricare alte configuratii fiind imposibile si solutia globala este evident ca este unica.

Permsplit

Problema poate fi abordata invers si anume daca se dau N multimi dinstincte (ce contin numere naturale de la 1 la N) exista un mod de unire a oricaror doua multimi consecutive astfel incat la final sa se obtina multimea numerelor naturale aflate intre 1 si N?

Pentru rezolvarea acestei abordari a problemei se va folosi o stiva. La fiecare stare se pastreaza o multime compacta care cuprinde toate numerele intre doi indici. La fiecare pas se adauga in stiva un nou interval format din noua multime (formata dintr-un singur element) si se compacteaza in jos pe stiva cat timp intervalele se pot compacta (astfel formand o noua multime compacta). Daca la final stiva contine numai o singura multime (si anume cea care contine toate numerele naturale cuprinse intre 1 si N) exista solutie. Afisarea multimilor ce se unesc se realizeaza invers cronologic.

stiva.push(make_interval(A[1],A[1]));

for(int i=2;i<=N;i++)
{
   interval x = make_interval(A[i],A[i]);

   while(sePoateCombina(x,stiva.top()))
   {
       x = combine(x,stiva.top());
       stiva.pop();
       stiva.push(x);
   }
}

Return of the MVC

Doua moduri triviale de a aborda aceasta problema sunt tehnicile greedy si backtracking. Pentru rezolvarea problemei vom explica numai a doua tehnica, prima nefiind neaparat standard si in plus difera in functie de optimizari, dar niciuna dintre cele doua nu vor obtine punctajul maxim.

Pentru inceput putem sa folosim tehnica backtracking sa generam pe rand toate combinarile de N luate cate i noduri, cu i de la 1 la 18. Se genereaza doar pana la 18 pentru ca acesta este numarul maxim de noduri pentru o acoperire minima precizat in enuntul problemei. Orice optimizare aplicata asupra acestui algoritm va conduce la acelasi rezultat.

Solutia corecta foloseste aceeasi tehnica de mai devreme, dar cu urmatoarea observatie: Dintre oricare doua noduri legate printr-o muchie trebuie ales obligatoriu exact unul si numai unul.
De aici putem gandi backtracking-ul in felul urmator. Vom pastra o multime de noduri in care putem adauga si scoate usor elemente. La fiecare pas al backtracking-ului vom cauta exact o singura muchie astfel incat sa nu aiba niciun capat in multime. In momentul in care gasim muchia respectiva vom adauga mai intai nodul stang in multime si vom continua backtracking-ul in apelul urmator, iar ulterior vom scoate nodul stang din multime, il vom adauga pe cel drept si vom apela din nou pasul urmator din backtracking. Vom opri backtracking-ul in momentul in care numarul de apeluri recursive depaseste valoarea 18 sau cea mai buna solutie gasita pana la momentul respectiv.

Complexitate teoretica finala 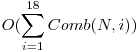, dar datorita observatiei prezentate mai sus algoritmul se comporta mult mai bine in practica.

Parb

Se pot incerca diverse solutii care incearca toate perechile de noduri (x, y) si se alege perechea cu sirul maxim, insa evident ca aceste solutii nu vor obtine punctaj maxim din cauza numarului mare de noduri.
Vom rezolva problema aplicand o strategie greedy.
Notam cu s sirul de caractere asociat nodurilor.
Putem tine un vector de perechi (start_lant, sfarsit_lant) cu lanturile care sunt la pasul curent candidate la solutie. Se observa ca daca perechea (x, y) este solutie atunci s[x] este cel mai mare caracter din s. Putem astfel sa consideram ca puncte de pornire pentru lantul nostru doar acele noduri care au s[node] = max(s[ 1 ], s[ 2 ], ..., s[n]).
Astfel, initial vectorul nostru de candidati contine perechile (node, node) pentru care node indeplineste conditia mentionata anterior.
Vom incerca acum sa extindem lanturile candidate cu inca o pozitie. Aplicand acelasi rationament observam ca un lant candidat la solutie (x, y) il putem extinde in (x, z) cu z fiu al lui y daca si numai daca s[z] = max(s[i]), cu i fiu direct al unui nod care e sfarsit de lant candidat la solutie. Repetam procedeul pana cand nu mai putem adauga noduri la niciun lant candidat la solutie (pana ajungem in frunze cu toate lanturile candidate).
Sa analizam acum putin comportamentul algoritmului nostru. Intuitiv se poate observa ca acesta s-ar comporta foarte rau pe cazul in care arborele nostru este un lant si toate nodurile au acelasi caracter asociat. In aceest caz, la pasul 1 vom avea n perechi candidate la solutie (toate nodurile au valoare maxima), la pasul 2 vom avea n - 1, la pasul 3 vom avea n - 2, ..., la pasul n vom avea o pereche. Observam ca algoritmul nostru ruleaza in 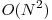in acest caz.
Sa presupunem ca ne aflam la un pas intermediar al algoritmului nostru si avem 2 perechi candidate (x0, y0), si (x1, y1) la solutie pe care vrem sa le extindem in z0 respectiv in z1. Sa analizam ce se intampla in cazul in care z0 = x1. Deoarece atat z0 cat si z1 pot fi noduri "de extindere" inseamna ca s[z0] = s[z1] adica s[x1] = s[z1]. Deducem ca la inceputul algoritmului nostru am avut perechea (z1, z1) candidata.
Exista acum 2 cazuri in care se poate incadra un lant extins din (z1, z1):
1. Lantul exista la pasul curent.
2. Lantul nu exista datorita faptului ca nu era optim.
Daca notam cu A sirul determinat de lantul (x0, y0) care e acelasi cu cel determinat de (x1, y1) si cu B sirul determinat de lantul (z1, sfarsit_lant) observam ca din x0 putem crea sirul AAB, iar din x1 AB. Observam ca indiferent de cazul in care ne aflam, daca extindem lantul (x1, y1) nu putem obtine o solutie mai buna decat din (x0, y0). Astfel deducem ca lantul (x1, y1) este irelevant si il putem elimina din vectorul de candidati.
Aceasta solutie obtine 100 de puncte.

Mai Marii Orasului

Pentru inceput, vom rezolva problema presupunand ca se poate trece o singura data prin fiecare muchie. In acest caz, raspunsul ar fi suma tututor muchiilor din graf. Cum fiecare muchie are costul pozitiv, este raspunsul maxim pe care-l poate admite problema. Se poate trece o singura data prin fiecare muchie cand graful admite un ciclu eulerian.

Mai departe vom face urmatoarea observatie: costul obtinut vizitand o muchie de doua ori este cel putin la fel de bun decat costul obtinut daca nu am vizita muchia deloc. Pe de alta parte, daca vizitam o muchie de 3 sau mai multe ori, costul total va scadea, deci in solutia optima fiecare muchie e vizitata o data sau de 2 ori.

Costul unei solutii este suma costurilor tuturor muchiilor minus costul muchiilor vizitate de 2 ori. Pentru a obtine cost maxim, trebuie ca suma costurilor muchiilor vizitate de 2 ori sa fie cat mai mica. Problema se reduce la a transforma graful intr-unul eulerian folosind urmatoarea operatie: "dublam" o muchie deja existenta (ca si cum am mai adauga-o odata in graf) si adaugam costul muchiei la costul muchiilor vizitate de 2 ori (evident, acest cost trebuie sa fie minim).

Un graf este eulerian atunci cand toate gradele nodurilor sunt pare. Va trebui sa alegem toate nodurile cu grad impar si sa le crestem gradul cu 1. Sa presupunem ca A si B sunt 2 noduri cu grad impar si X, Y, Z nodurile aflate pe drumul dintre ele (drumul este deci A - X - Y - Z - B)

Putem adauga inca o muchie intre A - X, X - Y, Y - Z, si Z - B, astfel toate nodurile vor avea grade pare, intrucat pentru orice nod de pe drumul dintre A si B, excluzand capetele, vom adauga doua muchii noi adaugate, paritatea gradelor acestor noduri nu se schimba. Se contureaza urmatorul algoritm: alegem 2 noduri care au grad impar, alegem un drum intre ele si "dublam" muchiile drumului. Mai raman 2 probleme de rezolvat:

1. Odata fixate nodurile A si B, cum alegem drumul dintre ele?
2. Cum cuplam nodurile doua cate doua?

Ca sa creasca costul cat mai putin, pentru a raspunde la 1. putem aplica o strategie greedy: alegem cel mai scurt drum intre A si B. Cel mai scurt drum intre oricare 2 noduri poate fi calculat cu algoritmul Roy Floyd. Ar fi o problema cu acest greedy: daca 2 noduri A, B si C, D isi aleg o muchie comuna in drumul lor cel mai scurt. Muchia ar fi parcursa de 3 ori, ceea ce am stabilit ca nu e optim. Daca o muchie apare in 2 drumuri, inseamna ca nodurile nu sunt imperecheate cum trebuie, si exista o alta imperechere, cu cost mai bun, in care muchiile din cel mai scurt drum sa apara pentru o singura pereche de noduri (incercati sa gasiti un contra exemplu, daca puteti crea unul :p).

Restrictia N <= 18 ne sugereaza ca nu exista algoritm polinomial pentru imperechere (sau cel putin mai marii comisiei nu au gasit unul). In schimb, se poate folosi o dinamica pe biti. Fie DP[mask] = costul minim al muchiilor parcurse de 2 ori, astfel incat nodurile care au bitul 1 in masca sunt deja imperecheate. Evident, vom considera doar nodurile cu grad impar. Pentru o valoare mask, alegem 2 biti i si j astfel incat in masca sa aiba valoarea 0 si actualizam costul lui DP[mask | (1 << i) | (1 << j)] cu DP[mask] + shortest_path(i, j). Raspunsul este suma costurilor muchiilor - DP[(1 << n) - 1].

Complexitatea este O(2^N * N²).

Probleme asemanatoare:
http://www.math.bas.bg/infos/files/2010-11-27-A1-en.pdf
http://codeforces.com/contest/429/problem/E

Timetravel