Solutii Algoritmiada 2013, Runda 2
- Lista de probleme
- Dmin2
- Queue
- Mergesort
- Citylog
- Circulatie
Dmin2
Observam ca in graful initial nu va exista un drum 1 - i - N. Deci, pentru orice luminis i din [2,N-1] exista doua cazuri: este legat de unul dintre nodurile 1 si N sau nu este legat de niciunul dintre ele. Toate luminisurile din al doilea caz le vom lega(mental) de unul dintre nodurile 1 si N si pentru fiecare adaugam 1 la solutie. Deci, toate nodurile se vor afla in primul caz. Daca notam cu G[i] gradul unui nod atunci se vor mai adauga un numar maxim de ![\frac{\sum\limits_{i=2}^{N-1}N-2-G[i]}{2} \frac{\sum\limits_{i=2}^{N-1}N-2-G[i]}{2}](http://www.infoarena.ro/static/images/latex/804e34f315a51d3cdb8f56152df13028_4.44841pt.gif) muchii. Impartirea la 2 vine de la faptul ca in acea suma fiecare muchie se numara de doua ori.
muchii. Impartirea la 2 vine de la faptul ca in acea suma fiecare muchie se numara de doua ori.
Queue
Presupunem ca avem x push_back() -uri si apoi x pop_front() -uri. Pentru a simula acest proces, introducem cele x elemente in stiva 1 si apoi pentru a simula scoaterea lor ar trebui sa le scoate in ordinea inversa a lor.
De aici ne vine ideea de a folosi stiva 1 ca si stiva de intrare si stiva 2 si stiva de iesire. Cand avem push_back(), introducem elementul respectiv in stiva 1. Cand avem pop_front(), luam primul element din stiva de iesire. In caz ca stiva de iesire e goala, golim toate elementele din stiva de intrare si le punem in ordine inversa in stiva de iesire.
O optimizare se bazeaza pe observatia ca nu putem avea mai mult de 15000 pop_front() -uri. Deci, nu vom folosi mai mult decat primele 15000 push_back() -uri.
Mergesort
Exista multe abordari la aceasta problema, toate constand in gasirea unei formule si implementand relatia de recurenta.
O prima observatie e ca raspunsul pentru un anumit interval (left, right) nu depinde decat de lungimea intervalului, deci putem trata doar lungimi de intervale.
Un interval de lungime L se imparte in doua subintervale: primul contine A numere si al doilea B numere, unde  si
si 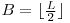 . Dupa cum spuneam, putem gandi problema in mai multe moduri.
. Dupa cum spuneam, putem gandi problema in mai multe moduri.
Varianta 1
Pentru fiecare lungime de interval valida, vom memora de cate ori se apeleaza functia in cazul in care acea lungime de interval e nesortata. Fie acest numar cnt[L]. Functia se va apela si pentru lungimile A si B, deci adaugam cnt[L] la cnt[A] si analog la cnt[B]. Acum vom calcula de cate ori se va apela recursiv functia din intervale de lungime L luand in calcul toate permutarile de ordin N. Exista combinari de N luate cate L moduri de a selecta elementele acestui interval, L! - 1 dintre ele sunt nesortate (si doar in cazul acestora se face apelul recursiv) si exista ! moduri de a aranja elementele din afara intervalului curent. Pe langa acestea, luam in considerare si faptul ca exista mai multe moduri de a ajunge la un interval de lungime L, la fel si faptul ca daca intervalul e nesortat, vor fi doua apeluri recursive. Deci, pentru fiecare interval de lungime L vom adauga la rezultat ![2 \cdot cnt[L] \cdot C_N^L \cdot (L! - 1) \cdot (N - L)! 2 \cdot cnt[L] \cdot C_N^L \cdot (L! - 1) \cdot (N - L)!](http://www.infoarena.ro/static/images/latex/418797fce7e28a7952cbf03806f86128_3.75433pt.gif) . Vom adauga in final N! la rezultat, deoarece nu am numarat apelurile initiale.
. Vom adauga in final N! la rezultat, deoarece nu am numarat apelurile initiale.
Varianta 2
Ne definim o functie recursiva F(L) care rezolva problema pentru un interval de lungime L. Exista combinari de L luate cate A moduri de a alege elementele din subintervalul din stanga. Pentru fiecare permutare a elementelor din A exista F(B) moduri de a alege elementele din B. E valabil si invers. Pana acum am calculat cate apeluri recursive se fac. La asta, mai adaugam L! deoarece sunt L! permutari ale intervalului de lungime L cu care se fac apelurile. Observam ca am calculat permutarea identica de trei ori. De aceea, scadem 2 din rezultat. Deci, 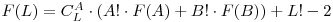 .
.
Oricare abordare am alege, daca precalculam factorialele si invers modularele, complexitatea solutiei este 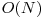 .
.
Citylog
Solutia 1: Timp 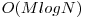 Memorie
Memorie 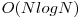
Nu putem rezolva aceasta problema folosind ideea de la problema Cerere (parcurgere in adancime) deoarece nu cunoastem dinainte query-urile. Deci, va trebui sa alegem o abordare asemanatoare cu cea de la problema Stramosi (al 2k-lea stramos). Pentru o operatie de tip 0, calculam al 2k-lea stramos al lui X pentru fiecare k valid. Pentru o operatie de tip 1, aflam raspunsul folosind valorile calculate anterior (pentru detalii consultati problemele mentionate anterior). Insa, din cauza limitei de memorie, aceasta abordare obtine 50 de puncte. Pentru 100 putem retine pentru fiecare nod al 10k-lea stramos, ceea ce ne reduce semnificativ memoria, dar la complexitatea fiecarei operatii apare constanta 10.
Solutia 2: Timp 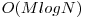 Memorie
Memorie 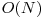
Aceasta solutie se bazeaza pe faptul ca nu trebuie sa precalculam stramosii pentru toate nodurile, ci doar pentru aproximativ 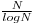 dintre ele. Cand adaugam un nod nou, ii precalculam stramosii doar daca cel mai apropiat nod precalculat e la distanta cel putin logN. La un query in care suntem la nodul x si trebuie sa-i aflam al y-lea stramos exista 3 situatii:
dintre ele. Cand adaugam un nod nou, ii precalculam stramosii doar daca cel mai apropiat nod precalculat e la distanta cel putin logN. La un query in care suntem la nodul x si trebuie sa-i aflam al y-lea stramos exista 3 situatii:
1. Ne aflam intr-un nod precalculat. Fie b cel mai semnificant bit al lui y. Mergem la al 2b-lea stramos al lui x si setam bitul b al lui y la 0.
2. Nu ne aflam in nod precalculat, iar cel mai apropiat stramos precalculat este mai jos decat y. Mergem la acel stramos si scadem din y diferenta de nivel.
3. Nu ne aflam in nod precalculat, iar cel mai apropiat stramos precalculat este mai sus decat y. In acest caz putem merge din tata in tata pana ajungem la al y-lea stramos al lui x, deoarece vom face maximum logN pasi.
Circulatie
Fiecare nod are gradul 3. Pentru ca suma costurilor muchiilor care intra in nod sa fie egala cu suma costurilor muchiilor care ies din nod trebuie ca muchiile incidente unui nod sa ia valorile (1, 1, -2) sau (1, 2, -3).
Deoarece fiecare nod are acelasi grad, exista cuplaj perfect. Dupa ce am aflat cuplajul, putem considera muchiile din cuplaj avand valoarea -2 si celelalte doua 1. Datorita modului in care e definit cuplajul, e garantat ca fiecare nod va avea o singura muchie incidenta cu valoarea -2 si ca celelalte doua vor avea valoarea 1.
