Solutii Algoritmiada 2013, Runda 1

Kinetic

Observatia care ne duce la solutie este ca fiecare punct se intalneste cel mult odata cu alt punct, deci exista 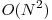O(N^2) momente in care se schimba ordinea relativa a punctelor. Parcurgem toate perechile de puncte si aflam momentul in care isi schimba pozitia relativa (poate sa nu existe acest moment). Sortam aceste momente, precum si lista query-urilor dupa t si le parcurgem in paralel pastrand lista punctelor sortata. Deci, daca stim ca la momentul 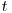t lista punctelor e sortata dupa 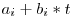a_i + b_i * t, atunci putem cauta binar punctele extreme care se afla in interiorul intervalului [x,y]. Complexitatea finala este O( N^2 logN^2 + MlogN)  .

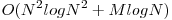Critice2

Construim arborele DFS al grafului. O muchie x->y este critica daca nu exista nicio muchie care porneste din subarborele lui y si ajunge intr-un nod cu nivelul mai mic sau egal cu x.
Putem sa ne folosim de faptul ca numarul mediu de muchii este o functie liniara si asta ne permite sa luam fiecare muchie separat. Daca o muchie are probabilitatea p de a fi critica, adaugam 1 * p la rezultat.
Aparitia unor muchii fictive ar putea strica structura de arbore DFS (care contine doar muchii de inaintare si muchii de intoarcere), insa ne salveaza urmatoarea observatie: daca ar fi sa adaugam in arbore o muchie transversala x-y, este echivalent cu a adauga doua muchii, una de la LCA (x,y) la x si una de la LCA (x,y) la y.

O prima idee ar fi sa facem un DFS in care, pentru fiecare nod care are tata, adaugam la rezultat probabilitatea ca muchia dintre acesta si tatal sau sa fie critica. Aceasta probabilitate o putem afla inmultind probabilitatile de a nu aparea (1 - probabilitatea de a aparea) a muchiilor care pornesc din subarborele nodului curent si ajung deasupra lui. Aceasta ar insemna ca din fiecare nod mai facem o parcurgere DFS in subarborele sau, deci complexitatea este 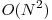O(N^2). Aceasta abordare obtine 70 de puncte.

Putem sa redenumim nodurile arborelui astfel incat fiecarui subarbore sa ii corespunda o succesiune de indecsi consecutivi. Asta ne permite sa tinem doi arbori de intervale : unul care ne permite sa aflam daca intr-un anumit subarbore exista o muchie care ajunge deasupra radacinii acestuia si altul pentru probabilitatea sa nu existe o muchie fictiva cu aceeasi proprietate. Functia care calculeaza rezultatul ar arata cam asa:

DFS(nod, tata)
  Pentru fiecare fiu x al lui nod
    DFS(x, nod)

  Pentru toate muchiile care pornesc din nod si merg deasupra lui tata
    Actualizeaza arborele de intervale pentru muchiile "sigure"
  Pentru toate muchiile care pornesc din nod si sub orice fiu al lui nod
    Actualizeaza arborele de intervale pentru muchiile "sigure"
    (stergem muchiile adaugate anterior deoarece acestea nu mai respecta conditia)

  Facem aceleasi doua operatii pentru muchiile fictive

  Daca nu exista nicio muchie "sigura" in subarborele lui nod care merge peste tata
    Scoate din arborele de intervale probabilitatea ca muchia nod-tata sa fie critica si adauga la rezultat

Daca LCA-ul e implementat in 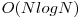O(NlogN), aceasta abordare are complexitatea 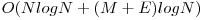O(NlogN + (M + E)logN) si obtine 100 de puncte.

La ambele abordari trebuie sa avem grija la muchiile care se repeta si la muchiile de la un nod la el insusi. Pe cele din urma le putem ignora. Singurul loc in care ne incurca primele e atunci cand un nod are doua muchii catre tatal sau, caz in care nu are nicio sansa de a fi critica.

Taie

Interzis

Problema se poate rezolva cu programare dinamica. Starea este dp[i][j] = numarul de siruri de i caractere care se termina cu primele j caractere din L. La fiecare pas avem doua variante: fie punem 'a', fie 'b'. Daca caracterul respectiv e identic cu L[j] (al j+1-lea caracter din L) atunci adunam dp[i][j] la dp[i + 1][j + 1]. In caz contrar, adunam dp[i][j] la dp[i + 1][k], unde k este lungimea celui mai lung prefix al lui L care este egal cu sufixul lui L[0..j-1] (cu alte cuvinte, cate litere se mai potrivesc dupa ce am pus una nepotrivita). 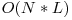Pentru a ajunge la complexitatea optima O(N * L), va trebui sa precalculam aceste pozitii. Raspunsul final va fi \sum\limits_{j=0}^{|L|-1}dp[N][j], unde |L| e lungimea sirului L.
Observam ca la orice moment avem nevoie de doar doua linii ale matricei. Deci, pentru a ne incadra in memorie le vom retine doar pe ultimele doua linii de care avem nevoie.

Mvc

Putem reduce problema la o forma mai simpla cu ajutorul unor observatii. Observam ca graful este conex are N noduri si N muchii. Daca ar avea N - 1 muchii ar fi un arbore, deci acea muchie in plus va forma un ciclu.
Presupunem ca am scapat de acel ciclu si ca am transformat graful in arbore. Pentru a alege nodurile astfel incat fiecare muchie sa aiba incident cel putin un nod ales, fiecare nod trebuie sa respecte urmatoarea conditie: daca acesta nu este ales, atunci trebuie alesi toti fiii acestuia; daca este ales, atunci putem decide ce facem cu fiii lui. Deoarece graful este un arbore, putem rezolva aceasta subproblema prin programare dinamica. Starea este dp[i][j] = costul minim pentru a satisface conditiile din enunt pentru subarborele cu radacina in i. Daca j este 0, inseamna ca nu am ales nodul i, 1 in caz contrar.
Revenind la graful care contine un ciclu: cautam una dintre muchiile din ciclu si trebuie sa alegem neaparat unul dintre capetele ei. Incercam ambele variante. Dupa ce am fixat nodul ales, eliminam muchia din graf si problema se reduce la subproblema mentionata anterior.
Complexitate 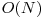O(N).

Mutari

Prima data trebuie sa verificam daca exista solutie sau nu. Observam ca A(1) trebuie sa il divida pe A(2) (altfel A(2) nu ar putea ajunge la 0). Datorita acestui fapt, A(2) va fi un multiplu de A(1) pe tot parcursul jocului. Deci, si A(3) va fi multiplu de A(1). Continuand rationamentul, rezulta ca, pentru a avea solutie, toate elementele trebuie sa fie divizibile cu A(1).
Solutia se poate construi in felul urmator: cat timp avem elemente nenule in afara de A(1) parcurgem invers elementele pornind de la ultimul element nenul. Pentru fiecare A(i) scadem cat mai mult posibil din A(i+1), avand grija ca A(i+1) sa nu ajunga la 0 decat daca nu exista elemente nenule dupa el (fiindca astfel ar ramane nenule).