Solutii Algoritmiada 2012, Runda 3

• Lista de probleme
• Bal
• Controlor
• Paginatie
• Swaps
• Xspe

Bal

Problema cere sa se determine daca exista un singur (unul si numai unul) cuplaj perfect, intr-un graf bipartit, cu n noduri de fiecare parte. Este clar ca daca un baiat nu si-a exprimat nicio preferinta, atunci nu exista solutie. Nu exista nicio solutie nici daca exista o fata care nu este admirata de niciun baiat (in cazul asta, fata nu va fi invitata la bal, iar celelalte n - 1 fete nu vor ajunge pentru a fi cuplate cu n baieti). Daca vreun baiat are o singura preferinta sau o fata are un singur admirator, atunci, in cazul in care exista solutie, acestia vor fi cuplati cu acea preferinta/admirator unic(a). Daca fiecare baiat are cel putin 2 fete pe care doreste sa le invite la bal si fiecare fata are cel putin 2 admiratori, atunci sau exista solutie multipla, sau nu exista solutie. De aceea, se poate apela la o strategie recursiva, prin care mai intai se verifica daca toate nodurile au gradul cel putin egal cu 2 sau egal cu 0, caz in care graful are mai multe cuplaje sau niciunul, altfel se cupleaza nodul cu grad 1 cu singurul lui nod adiacent, iar raspunsul va fi dat de graful rezultat prin eliminarea nodului cu grad 1 si cel adiacent lui.

Pentru a obtine 100 de puncte, algoritmul trebuie implementat nerecursiv si cat mai eficient cu putinta (O(n + m)). Hint: se poate folosi o coada simpla pentru a tine nodurile din graf care au grad 1, care se initializeza imediat dupa citire si care se actualizeza de fiecare data cand se face o eliminare in graf. Nu e necesar sa se faca stergerea propriu-zisa din lista de adiacenta, ajunge sa se marcheze nodurile ca fiind sterse. Atentie: o muchie poate aparea de mai multe ori!

Iata o demonstratie a faptului ca daca fiecare baiat are cel putin 2 preferinte, atunci sau nu exista nicio solutie, sau exista mai mult de una. Se presupune prin absurd ca exista o singura solutie. Fara a restrange generalitatea demonstratiei, se poate spune ca aceasta solutie cupleaza baiatul 1 cu fata 1, baiatul 2 cu fata 2, etc (se decide, pentru a nu incarca demonstratia, ca baiatul 1 are ca si preferinta pe fata 1, etc). Se construieste o alta solutie in modul urmator: fie X₁ un baiat oarecare. El are si alta preferinta in afara de fata X₁ (fiecare baiat are cel putin 2 preferinte), fie ea fata X₂ ≠ X₁. Baiatul X₂ are si alta preferinta decat fata X₂, fie ea fata X₃ ≠ X₂, etc. Se poate obtine astfel un sir infinit (X₁, X₂, ...), cu valori in {1, 2, .., N} - deci la un moment dat o valoare se repeta. Daca X_k este prima valoare care apare de 2 ori, adica exista (X_k, X_k+1, X_k+2, .., X_m-1, X_m = X_k) parte a sirului initial, atunci o alta solutie se poate obtine folosind (baiat X_k, fata X_k+1), (baiat X_k+1, fata X_k+2), ..., (baiat X_m-2, fata X_m-1), (baiat X_m-1, fata X_k), iar in rest pastrand (baiat i, fata i), pentru i diferit de X_k, .. X_m-1.

Controlor

Fie A'[i][i + j] = A[i][j]. Mai exact, elementul A'[i][j] va reprezenta "cati calatori urca la statia i si coboara la statia j". Pentru matricea A din exemplu matricea A' va arata in modul urmator:

10 8 7 5
  0 5 6 4
  0 0 3 3
  0 0 0 2

Se observa ca pentru o intrebare de forma (P, Q) vor conta doar liniile cu indice i astfel incat P <= i <= Q, deoarece calatorii de pe liniile cu i > Q vor intra dupa ce Miruna verifica biletele. De asemenea, vor conta doar coloanele cu j >= Q, deoarece aceia care au j < Q au iesit din tren inainte ca Miruna sa verifice biletele.
In concluzie, problema se reduce la a afla pentru fiecare (P, Q) suma numerelor din submatricea cu coltul stanga sus (P, Q) si dreapta jos (Q, N).
In matricea din exemplu, raspunsul pentru intrebarea (2, 2) va fi suma numerelor ingrosate:
10 8 7 5
  0 5 6 4
  0 0 3 3
  0 0 0 2
Pentru intrebarea (2, 3) raspunsul va fi suma numerelor:
10 8 7 5
  0 5 6 4
  0 0 3 3
  0 0 0 2
Fie Sol[P][Q] raspunsul pentru intrebarea (P, Q). Se observa din exemplele de mai sus ca, daca se considera Sol[P][Q] = 0 pentru Q < P, atunci Sol[P][Q] = Sol[P + 1][Q] + A'[i][j] + A'[i][j + 1] + ... + A'[i][N]. Daca se va precalcula matricea Sum, reprezentand matricea sumelor partiale pe fiecare linie, atunci recurenta va deveni Sol[P][Q] = Sol[P + 1][Q] + Sum[i][j]. Precalcularea matricii Sum si aflarea matricii Sol se pot face in complexitate O(N²).

Complexitate finala: O(N²)

Paginatie

Restrictia de memorie nu permite mentinerea in memorie a tuturor cuvintelor, dar se pot retine cuvintele ce urmeaza a fi afisate pe un singur rand, deoarece fiecare linie are maxim 1000 de caractere ceea ce limiteaza numarul de cuvinte ce pot aparea pe un rand la 500, astfel se pot retine cuvintele neafisate intr-o matrice de caractere de dimensiune 500×51. La fiecare cuvant citit, se verifica daca, adaugandu-l la randul din care fac parte cuvintele precedente, nu se depaseste limita de caractere y, cuvantul fiind adaugat doar daca se respecta conditia (suma lungimilor cuvintelor de pe ultimul rand) + (lungimea cuvantului curent) + (numarul de cuvinte de pe randul precedent) <= y, unde este necesara adunarea (numarului de cuvinte de pe randul precedent) deoarece acesta este numarul minim de spatii ce poat fi folosite. Daca nu se respecta conditia, se vor afisa cuvintele retinute in matrice pe un rand, iar cuvantul curent va fi adaugat in matrice pe pozitia 0, aceasta fiind refolosita pentru retinerea cuvintelor de pe linia urmatoare. La final se vor afisa pe o linie cuvintele neafisate pana acum.
Afisarea cuvintelor pe un rand se va face in modul urmator:
Fie L lungimea cuvintelor, iar N numarul lor. Daca N = 1, atunci se va afisa pur si simplu singurul cuvant, daca N > 1, dupa fiecare din primele (y - L) mod N cuvinte se vor afisa (y - L) / N + 1 spatii, iar dupa restul, in afara de ultimul, se vor afisa (y - L) / N spatii.
De retinut sa se afiseze un rand gol dupa fiecare x randuri de cuvinte.

Swaps

Inainte de a incepe rezolvarea implicita a problemei sunt necesare 4 observatii:
1. Numarul de interschimbari posibile este N²
2. Probabilitatea ca la un pas sa aibe loc o interschimbare fixa (intre doua pozitii diferite) este P1 = 2 / N²
3. Probabilitatea ca la un pas sa aibe loc o interschimbare care sa implice o pozitie fixa p este (2 * N - 1) / N², deci probabilitatea ca la un pas sa aibe loc o interschimbare care sa nu contina o pozitie fixa p este P2 = 1 - (2 * N - 1) / N².
4. Probabilitatea ca la un pas sa aiba loc interschimbarea (x, x) pentru orice 1 <= x <= N este P3 = 1 / N².

I. Solutia de complexitate O(T * N² * P) (care se poate reduce la O(T * N * P)), de la care porneste si ideea buna, consta in construirea unei dinamici d[i][j] = probabilitatea ca numarul aflat initial pe pozitia A sa ajunga pe pozitia j dupa primele i interschimbari. Este necesara initializarea liniei 0 (0 in toate pozitiile in afara de A, unde este 1). Recurenta se obtine destul de usor : d[i][j] = d[i - 1][j] * (P2 + P3) + P1 * (d[i - 1][1] + ... + d[i - 1][j - 1] + d[i - 1][j + 1] + ... + d[i - 1][N]).

II. O alta solutie care are complexitate mai buna, O(T * N² * log P), consta in construirea unei matrice M (de dimensiune N x N) de forma:

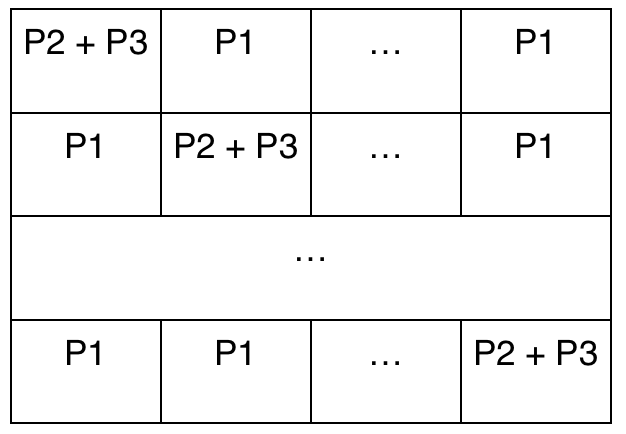
Se observa ca prin inmultirea lui d[0] (linia 0 a dinamicii anterioare) cu M se obtine d[1]. Pe caz general d[P] = d[0] * M^P. Tot ceea ce a mai ramas de facut este ridicarea matricei M in timp logaritmic la puterea P.

III. Solutia de complexitate O(T * P) se bazeaza pe cea anterioara, doar ca mai este necesara o observatie: matricea M ridicata la orice putere isi va pastra forma (pe diagonala principala un numar x si in rest un numar y). Problema se reduce la aflarea celor 2 siruri a_n si b_n ce caracterizeaza matricea Mⁿ. Prin inmultirea lui Mⁿ cu M se observa ca:
a_(n + 1) = a_n * (P2 + P3) + b_n * P1 * (N - 1)
b_(n + 1) = a_n * P1 + b_n * (P2 + P3) + b_n * P1 * (N - 2) = a_n * P1 + b_n * (P1 * (N - 2) + P2 + P3)
Valoarea a_n va reprezenta "probabilitatea ca, dupa n interschimbari, elementul x (oarecare) sa ajunga pe pozitia x", iar b_n va fi "probabilitatea ca, dupa n schimbari, elementul x sa ajunga pe o pozitie diferita de x".
Pentru fiecare dintre cele T query-uri se calculeaza in O(P) valoarea lui a_P daca A = B sau valoarea lui b_P altfel.

IV. Solutia ce obtine 100 de puncte are complexitate O(T * log P) si foloseste ridicarea de matrice la putere in timp logaritmic. Tinand cont de recurentele obtinute anterior, avem nevoie de urmatoarea matrice, L:

Xspe

Problema cere sa se afle cea mai mare suma A[i] + A[p(i)], unde p(i) este cel mai mic indice mai mare decat i astfel incat A[p(i)] < A[i] pentru orice 1 <= i <= N. Presupunem ca A[N + 1] = 0.
Pentru ca pentru fiecare element conteaza doar numerele de dupa el, o idee buna este sa se porneasca de la coada si sa se tina o structura astfel incat sa se calculeze indicele p(i) pentru fiecare pozitie i eficient. Presupunem ca algoritmul a ajuns la pozitia i. Se observa ca pentru urmatorii pasi (adica pentru elementele de pe pozitiile 1, 2, ... i - 1, elementul A[i] va invalida anumite valori prin care am trecut deja. Mai exact, pentru orice A[j] cu j <= i, elementele de la i la dreapta mai mari sau egale cu A[i] nu vor mai putea constitui al doilea element din pereche, adica elementul cu indicele p(j). De aceea se pot elimina toate numerele parcurse care sunt mai mari sau egale cu A[i]. Presupunand ca aceste numere sunt tinute intr-o stiva in ordinea parcurgerii lor, se observa ca daca se fac aceste eliminari la fiecare pas, stiva cu elemente va ramane mereu sortata crescator, de aceea numerele ce vor fi sterse la fiecare pas vor fi in varful stivei, iar p(i) va fi chiar indicele ultimului element adaugat in stiva.

Complexitatea finala este O(N) deoarece fiecare element e introdus si scos din stiva doar odata.