Revizia anterioară Revizia următoare
Teoria jocurilor
(Categoria Teoria jocurilor, Autor Filip Cristian Buruiana)
- Capitole
- Notiuni de baza
- Jocul NIM
- Numere Sprague-Grundy
- Adunarea jocurilor
- w-numere
- Aplicatii si probleme
Teoria jocurilor
(Categoria Teoria jocurilor, Autor Filip Cristian Buruiana)
- Capitole
- Notiuni de baza
- Jocul NIM
- Numere Sprague-Grundy
- Adunarea jocurilor
- w-numere
- Aplicatii si probleme
Jocul NIM
 Probabil cel mai cunoscut joc impartial este jocul NIM. In acest joc, se considera N gramezi, fiecare gramada avand un numar de pietre. La fiecare pas, jucatorul aflat la mutare elimina un numar nenul de pietre (eventual toate) dintr-o singura gramada. Jucatorii muta alternativ. Castigatorul este cel care ia ultimele pietre. De obicei, jocul NIM se joaca cu 3 gramezi de pietre, insa strategia de castig este aceeasi indiferent de numarul gramezilor.
Probabil cel mai cunoscut joc impartial este jocul NIM. In acest joc, se considera N gramezi, fiecare gramada avand un numar de pietre. La fiecare pas, jucatorul aflat la mutare elimina un numar nenul de pietre (eventual toate) dintr-o singura gramada. Jucatorii muta alternativ. Castigatorul este cel care ia ultimele pietre. De obicei, jocul NIM se joaca cu 3 gramezi de pietre, insa strategia de castig este aceeasi indiferent de numarul gramezilor.
Operatia exclusive-or
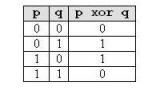
Pentru a determina strategia de castig ne vom folosi de operatia xor (exclusive or) si proprietatile ei. Aceasta operatie se realizeaza prin operatorul ^ in C/C++, si prin xor in Pascal. Ca operatie pe biti, ea poate fi interpretata ca adunare in baza 2 fara transport, dupa cum reiese din tabelul alaturat.
Atunci cand facem xor intre numere naturale trebuie mai intai sa transformam aceste numere in baza 2, si apoi sa adunam fara transport bitii de pe fiecare pozitie. De exemplu, 1 xor 7 xor 5 = 3, deoarece avem:
1 = (001)2 xor
7 = (111)2
5 = (101)2
______________
(011)2 = 3
Strategia de castig
Pe baza operatiei xor, strategia de castig pentru NIM poate fi formulata conform urmatoarei teoreme:
Teorema: Fie N gramezi. Prima gramada are x1 pietre, cea de a doua x2, si asa mai departe, pana la ultima care are xN pietre. O astfel de pozitie este pierzatoare in jocul de NIM daca si numai daca suma-xor a numerelor de pietre din gramezi este 0, adica daca x1 xor x2 ... xor xN = 0.
Pentru a demonstra aceasta teorema, trebuie sa aratam ca dintr-o stare cu suma-xor egala cu 0 (pierzatoare), oricum am muta, nu putem ajunge decat intr-o stare cu suma-xor nenula (castigatoare), si ca dintr-o stare castigatoare putem efectua o mutare in mod convenabil astfel incat sa ajungem intr-o stare de pierdere.
Sa presupunem prin reducere la absurd ca dintr-o stare cu suma-xor 0 putem ajunge in alta stare care are suma-xor tot 0. Selectam o gramada oarecare cu y pietre si dorim sa eliminam un numar de pietre din aceasta gramada. Daca notam cu S suma-xor a numerelor de pietre din celelalte N-1 gramezi neselectate, atunci avem S xor y = 0. Dar a xor b = 0 daca si numai daca a = b, deci S = y. Daca din gramada selectata eliminam x pietre, 0 < x ≤ y, pentru a ajunge intr-o stare tot cu suma-xor 0 trebuie sa avem S xor (y-x) = 0, echivalent cu S = y-x. De aici si din S = y rezulta ca x = 0, fals, deoarece nu putem elimina 0 pietre. Deci oricum am efectua o mutare dintr-o stare de pierdere vom ajunge intr-o stare castigatoare.
Ramane de demonstrat ca din orice stare de castig putem sa aducem adversarul intr-o stare pierzatoare. Fie S suma-xor a marimilor celor N gramezi. Daca exista o gramada cu y pietre astfel incat y > y xor S, atunci putem elimina y - y xor S pietre din aceasta gramada, ramanand cu y - (y - y xor S) = y xor S pietre. Din gramada cu y pietre am obtinut o gramada cu y xor S pietre, deci noua suma-xor va fi obtinuta din cea veche (S) xorata cu ea insasi: (... xor y) xor S = S xor S = 0. In consecinta, daca exista o gramada cu proprietatea de mai sus, atunci putem ajunge din orice stare de castig in una de pierdere. Fie p pozitia celui mai semnificativ bit din reprezentarea binara a lui S. Printre cele N gramezi, va exista cel putin una care are bitul de pe pozitia p egal cu 1 (altfel bitul p din S ar fi fost 0). Fie y numarul de pietre dintr-o astfel de gramada. Bitii de 1 din y si S de pe pozitia p se vor anula pentru ca 1 xor 1 = 0. Astfel, vom avea y > y xor S.

In consecinta, putem ajunge din orice stare de castig intr-o stare de pierdere. Teorema este astfel demonstrata.
Notiuni de baza | Jocul NIM | Numere Sprague-Grundy |
Adunarea jocurilor | w-numere | Aplicatii si probleme
Teoria jocurilor
(Categoria Teoria jocurilor, Autor Filip Cristian Buruiana)
- Capitole
- Notiuni de baza
- Jocul NIM
- Numere Sprague-Grundy
- Adunarea jocurilor
- w-numere
- Aplicatii si probleme
Numere Sprague-Grundy
Alaturi de jocul NIM, numerele Sprague-Grundy au o importanta deosebita in analiza jocurilor impartiale. Majoritatea acestora se poate reduce la urmatorul joc: "Se considera un graf orientat aciclic care contine un pion intr-un nod oarecare. Cei doi jucatori muta alternativ. Prin mutare se intelege miscarea pionului din nodul in care se afla intr-un nod adiacent. Jucatorul care nu mai poate muta pierde."
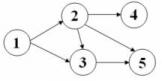
De exemplu, pentru graful din figura alaturata, daca pionul se afla initial in nodul 1, primul jucator aflat la mutare va pierde in cazul unui joc perfect.
Cum graful este aciclic, jocul este finit si are intotdeauna un castigator. Daca in graf exista un singur pion, castigatorul poate fi determinat prin metoda programarii dinamice. Astfel, winx va fi true daca si numai daca primul jucator aflat la mutare are strategie de castig atunci cand pionul se afla in nodul x. Astfel, winx = true daca si numai daca exista un nod y astfel incat sa existe arc intre x si y si winy = false. In caz contrar, winx = false. Pentru exemplul de mai sus, win2 = true, iar win1 si win4 vor fi false. Valorile vectorului win se vor calcula in ordinea din sortarea topologica a nodurilor, in complexitate O(N + M), unde N este numarul de noduri iar M numarul de muchii din graful dat.
Totusi, daca in graf ar exista mai multi pioni, problema determinarii castigatorului nu mai poate fi rezolvata prin programare dinamica. Folosind teoria dezvoltata independent de Roland Percival Sprague (1936) si Patrick Michael Grundy (1939), putem reduce complexitatea jocului cu mai multi pioni la complexitatea analizei jocului cu un pion. Ca in algoritmul de programare dinamica de mai sus, se incearca determinarea pozitiilor castigatoare si a celor necastigatoare pentru un singur pion.
Definitie: Functia Sprague-Grundy pentru un graf G = (V, E) este o functie mex (minimum excludant) definita pe V cu valori in multimea numerelor naturale, unde mex(x) = minim(n ≥ 0 |n diferit de mex(y), oricare ar fi y vecin al lui x).
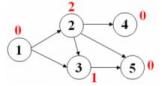 Altfel spus, valoarea Sprague-Grundy pentru un nod x al grafului aciclic dat este cel mai mic numar natural care nu este atribuit niciunui vecin al nodului x. Atribuirea valorilor se face incepand cu nodurile terminale, carora le este asociata valoarea 0. Valorile Sprague-Grundy pentru nodurile grafului de mai jos sunt scrise cu rosu in dreptul fiecarui nod.
Altfel spus, valoarea Sprague-Grundy pentru un nod x al grafului aciclic dat este cel mai mic numar natural care nu este atribuit niciunui vecin al nodului x. Atribuirea valorilor se face incepand cu nodurile terminale, carora le este asociata valoarea 0. Valorile Sprague-Grundy pentru nodurile grafului de mai jos sunt scrise cu rosu in dreptul fiecarui nod.
Se observa ca pozitiile care au valoarea Sprague-Grundy egala cu 0 sunt pierzatoare, in timp ce restul pozitiilor sunt castigatoare. Aceasta inseamna ca daca mex(x) = 0, in jocul cu un singur pion situat in nodul x jucatorul care muta primul nu are strategie sigura de castig, iar daca mex(x) este diferit de 0 atunci jucatorul care muta primul va castiga intotdeauna, in cazul in care joaca optim. Aceasta afirmatie este usor de demonstrat: daca mex(x) este diferit de 0 atunci exista un nod y, vecin al lui x, astfel incat mex(y) sa fie egal cu 0. In consecinta, primul jucator il va aduce intotdeauna pe adversarul sau in noduri care au valoarea Sprague-Grundy egala cu 0. Mai mult, primul jucator va ramane intotdeauna in noduri cu valoare diferita de 0, deoarece al doilea jucator nu il poate forta sa ajunga in aceste noduri: din nodurile cu valoarea 0 se poate ajunge doar in noduri cu valoarea nenula. In concluzie, jucatorul al doilea va pierde, deoarece va fi adus intr-un nod final (fara urmasi). La o analiza mai atenta se observa ca starile de joc respecta proprietatile pozitiilor castigatoare si pierzatoare, enuntate aici.
Valorile Sprague-Grundy se pot calcula si pentru jocuri in care nu apar precizate explicit grafuri. Fiecare stare posibila a jocului va fi un nod in graf, iar un arc va indica o posibila mutare: o trecere de la o stare la alta, conform regulilor existente.
Notiuni de baza | Jocul NIM | Numere Sprague-Grundy |
Adunarea jocurilor | w-numere | Aplicatii si probleme
Teoria jocurilor
(Categoria Teoria jocurilor, Autor Filip Cristian Buruiana)
- Capitole
- Notiuni de baza
- Jocul NIM
- Numere Sprague-Grundy
- Adunarea jocurilor
- w-numere
- Aplicatii si probleme
Adunarea jocurilor
Valorile Sprague-Grundy reprezinta o generalizare fata de algoritmul de programare dinamica in cazul jocului cu un singur pion, deoarece cu ajutorul acestor valori pot fi combinate mai multe jocuri. De exemplu, putem presupune ca in graful orientat sunt mai multi pioni in loc de unul singur si ca o mutare consta in deplasarea unui pion din nodul in care se afla intr-un nod adiacent. La fel ca mai sus, cine nu mai poate muta pierde. In acest caz, castigatorul in cazul unui joc perfect nu se poate determina pe baza programarii dinamice in timp polinomial. Mai mult, determinarea castigatorului nu este deloc triviala, asa cum era in cazul jocului cu un pion. Atunci cand combinam (adunam) mai multe jocuri elementare, rezultatul poate fi determinat in mod eficient cu ajutorul valorilor Sprague-Grundy.
In cazul jocului cu mai multi pioni, in loc sa consideram un singur graf, putem considera (conceptual) mai multe grafuri de joc identice, in fiecare dintre acestea aflandu-se cate un pion. Acum, o mutare inseamna alegerea unui graf si deplasarea pionului din graful ales conform regulilor pentru un singur pion. In acest fel, am separat jocul initial in mai multe jocuri independente. Stim rezultatul pentru fiecare joc independent in parte si dorim sa determinam castigatorul pentru jocul cu mai multe grafuri. Aceasta inseamna ca dorim sa combinam rezultatele partiale pentru a determina rezultatul general. Pentru aceasta vom folosi adunarea grafurilor de joc.
Sa presupunem ca avem P jocuri notate G1, G2, ..., GP, pe care dorim sa le adunam. Fiecare din cele P jocuri poate fi reprezentat ca un graf orientat fara circuite in care multimea nodurilor (notata Vi pentru jocul i) este data de multimea starilor iar multimea arcelor (notata Ei pentru jocul i) este data de perechile ordonate de stari adiacente (exista arc de la x la y daca se poate ajunge printr-o mutare din starea x in starea y). Adunand cele P jocuri obtinem un nou joc G pentru care o stare (nod in graful asociat) este un P-uplu (v1,v2, ...,vP) care ne precizeaza starea curenta pentru fiecare joc individual (vi este starea curenta in jocul i). Pentru a afla daca pentru o anumita stare din jocul G exista sau nu strategie sigura de castig am putea aplica algoritmul de programare dinamica (prezentat mai sus) pentru graful asociat jocului G. Se observa insa ca acest graf are |V1|*|V2|* ...*|VP| noduri, deci algoritmul nu este eficient.
In continuare vom arata cum putem sa determinam eficient daca o stare este castigatoare sau nu pentru un joc compus folosindu-ne de informatiile preprocesate pentru fiecare joc individual.
Adunarea xor
Vom aduna jocurile G1, G2, ..., GP astfel incat la fiecare pas jucatorul care urmeaza trebuie sa isi aleaga exact un joc si sa faca o mutare in jocul respectiv. Jucatorul care nu mai poate muta pierde. Un astfel de joc este generalizarea jocului cu un pion din capitolul precedent si se intalneste in problema Pawns, data la concursul national Bursele Agora. Pentru a determina castigatorul in cazul acestui joc, ne vom folosi de urmatoarea teorema:
Teorema: Fie jocurile independente G1, G2, ..., GP si fie G suma acestor jocuri. Daca la fiecare pas alegem un singur joc si efectuam o mutare in jocul ales, atunci o stare (v1,v2, ...,vP) din jocul G este pierzatoare daca si numai daca mex(v1) xor mex(v2) xor ... xor mex(vP) = 0, unde vi reprezinta starea din jocul Gi.
Demonstratie: Demonstratia este similara cu cea a jocului NIM, cele doua jocuri fiind asemanatoare. Starile care au suma-xor 0 sunt pierzatoare, celelalte stari fiind castigatoare.
Dintr-o stare pierzatoare putem ajunge numai in stari castigatoare. Prin reducere la absurd putem presupune ca mutam dintr-o valoare x = mex(vi) intr-o valoare x' = mex(v'i). Daca notam cu S suma xor a starilor din jocurile diferite de i, atunci avem S xor x = 0, deci S = x. Dar trebuie sa avem si S xor x' = 0, deci S este egal si cu x', ceea ce implica x = x'. Aceasta egalitate nu poate avea loc, deoarece dintr-o stare nu putem ajunge intr-o stare adiacenta care sa aiba aceeasi valoarea Sprague-Grundy (conform definitiei functiei mex).
Din orice stare castigatoare putem ajunge intr-o stare pierzatoare.
Vom arata ca jocul G este echivalent cu un joc NIM cu N gramezi in care gramada i are mex(vi) pietre. In jocul NIM putem alege o gramada cu mex(xi) pietre si sa luam cateva astfel incat in gramada sa ramana a<g(xi) pietre. Acestei mutari in jocul NIM ii corespunde o mutare in jocul compus G in care se alege jocul individual Gi si se muta din stare curenta xi intr-o stare y cu g(y)=a. Deoarece a<g(xi) va exista mereu o astfel de stare y. Nu vom lua in considerare mutarile cand dintr-o stare xi se muta intr-o stare y cu g(y)>g(xi) deoarece urmatorul jucator poate muta din starea y intr-o stare z cu g(z)=g(xi) si anuleaza practic mutarea precedentului. (de editat)
Notiuni de baza | Jocul NIM | Numere Sprague-Grundy |
Adunarea jocurilor | w-numere | Aplicatii si probleme
Teoria jocurilor
(Categoria Teoria jocurilor, Autor Filip Cristian Buruiana)
- Capitole
- Notiuni de baza
- Jocul NIM
- Numere Sprague-Grundy
- Adunarea jocurilor
- w-numere
- Aplicatii si probleme
w-numere
In capitolul precedent am observat diferite modalitati de a aduna jocuri. Jucatorul care efectua ultima mutare in aceste jocuri compuse castiga. Putem extinde insa complexitatea jocurilor analizate, considerand ca pentru un joc compus G castigatorul este cel care castiga primul unul dintre jocurile independente care compun jocul G. Acest tip de joc este numit sugestiv "The Winner takes it all" (WTIA).
Definitie: Fie G suma jocurilor G1, G2, ..., GP. Jucatorul aflat la mutare alege unul din jocurile care il compun pe G si efectueaza o mutare in jocul ales. Intr-un joc de tip WTIA, daca unul din jucatori pierde un joc independent Gi, atunci el pierde intreg jocul G.
Jocul NIM pe nivele
Jocul NIM este un caz trivial daca se joaca dupa regulile WTIA, deoarece jucatorul care muta primul poate alege o gramada oarecare si sa ia toate pietrele din aceasta gramada, castigand astfel un joc independent (gramada din care s-a facut mutarea) si, implicit, tot jocul cu mai multe gramezi. Putem introduce insa urmatoarea variatie a jocului NIM, care nu este deloc triviala: "Fie N supergramezi de monede, fiecare supergramada fiind formata dintr-un numar oarecare de gramezi asezate una peste cealalta. La fiecare mutare un jucator alege o supergramada si ia cel putin o moneda din cea mai de sus gramada nevida. Cand un jucator ia ultimile monede dintr-o supergramada jocul se termina si acesta este declarat castigator."
Sa consideram un exemplu cu doua supergramezi. Prima dintre acestea contine gramezi de dimensiune 4, 9 si 3, de la baza inspre varf, iar a doua supergramada este compusa din doua gramezi de cate 2 si respectiv 5 pietre. Primul jucator poate alege sa elimine pietre din prima supragramada sau din cea de a doua. In cazul in care alege sa faca mutarea din prima supragramada, atunci el poate lua intre una si trei pietre din gramada din varf. Daca ia trei pietre, gramada de sus se goleste, iar noua gramada de la varf din care se vor face mutari in prima supergramada va contine 9 pietre.
Clasificarea pozitiilor
In acest joc NIM pe nivele identificam urmatoarele pozitii speciale (numite superpozitii):
- superpierzatoare, in care exista o supergramada care nu contine nicio gramada. In acest caz, jucatorul aflat la mutare este considerat pierzator.
- supercastigatoare, in care jucatorul la rand va castiga dintr-o singura mutare. Toate pozitiile care au cel putin o supergramada formata dintr-o singura gramada nevida sunt supercastigatoare deoarece un jucator poate goli aceasta supergramada la urmatoarea mutare, castigand jocul.
Toate celelalte pozitii (in care fiecare supergramada contine cel putin doua gramezi) sunt considerate normale.
Daca jucatorul aflat la mutare gaseste jocul intr-o pozitie superpierzatoare atunci a pierdut. Daca in schimb pozitia este una supercastigatoare, el va castiga dintr-o singura mutare. Daca jucatorul se afla intr-o pozitie normala, atunci el poate aduce jocul in alta pozitie normala sau intr-o pozitie supercastigatoare. Aducerea adversarului intr-o pozitie supercastigatoare va duce insa la pierderea jocului. In consecinta, jucatorul aflat in pozitii normale va muta doar in alte pozitii normale. Se observa ca atunci cand un jucator nu mai poate muta intr-o pozitie normala pierde jocul deoarece va fi obligat sa mute intr-o pozitie supercastigatoare.
Functia w
Pentru a determina daca dintr-o pozitie jucatorul aflat la mutare are strategie de castig vom introduce o functie w astfel:
Definitie: Functia w este o functie definita pe multimea starilor unui joc cu valori in multimea numerelor naturale reunita cu indicatorii speciali SC (pentru o pozitie supercastigatoare) si SP (pentru una superpierzatoare). Functia w se obtine astfel:
- w(x) = SP, daca x este o pozitie superpierzatoare
- w(x) = SC, daca exista o stare u astfel incat din x sa se poata ajunge in u printr-o mutare si w(u) = SP
- w(x) = minim(n ≥ 0 | n diferit de w(u), oricare ar fi u stare vecina a lui x pentru care w(u) este numar natural). Prin stare vecina se intelege ca se poate ajunge dintr-o singura mutare din x in u.
Altfel spus, pozitiile superpierzatoare vor avea asociat indicatorul SP, iar cele supercastigatoare indicatorul SC. Eliminand toate aceste pozitii speciale vom obtine un graf in care toate pozitiile sunt normale. Daca aplicam algoritmul functiei mex de determinare a valorilor Sprague-Grundy pe pozitiile ramase obtinem chiar valorile returnate de functia w pentru aceste pozitii.
Teorema: Asemanator cu functia mex, o pozitie x este pierzatoare daca si numai daca w(x) = SP sau w(x) = 0.
Demonstratie: Daca w(x) = SP, atunci evident x este o pozitie de pierdere. Daca w(x) este numar natural si w(x) > 0, atunci este posibil ca jucatorul la mutare sa mute intr-o pozitie y cu w(y) = 0 (conform definitiei). Dintr-o pozitie w(x) = 0 se poate muta numai in pozitii supercastigatoare sau in pozitii cu w(x) > 0 (intr-o stare superpierzatoare nu se poate muta, deoarece in aceste stari se poate ajunge doar din stari supercastigatoare). Dat fiind faptul ca jocul este finit, se va ajunge la situatia in care din pozitia w(x) = 0 nu mai exista decat mutari in pozitii SC.
Teorema: Fie un joc G definit ca adunarea de tip WTIA a jocurilor G1, G2, ... Gp. Pozitia x din jocul G, care este un p-uplu de forma (x1, x2, ... xp), unde xi este starea din jocul Gi, este pierzatoare daca si numai daca cel putin una din urmatoarele conditii este indeplinita:
1. exista un joc i astfel incat w(xi) = SP
2. pentru orice joc i, w(xi) este numar natural. In plus, w(x1) xor w(x2) xor ... xor w(xp) = 0.
Demonstratie: Vom verifica daca pentru aceasta impartire sunt indeplinite conditiile pentru P-pozitii si N-pozitii, prezentate aici. Daca exista un joc i astfel incat w(xi) = SP, atunci starea x este una terminala si este de pierdere. Mai mult, din orice pozitie pierzatoare neterminala conform impartirii de mai sus, oricum am efectua o mutare, vom ajunge intr-o pozitie castigatoare.
Toate pozitiile terminale x au un subjoc xi care este SP, altfel s-ar mai putea efectua mutari. Daca un jucator este intr-o pozitie pierzatoare atunci w(x) = SP sau w(x1) xor w(x2) xor ... xor w(xp) = 0. Primul caz a fost analizat mai sus. Daca un jucator muta in orice subjoc k atunci fie va muta intr-o pozitie supercastigatoare in acel joc, fie va muta intr-o pozitie y cu w(y) �w(xk). In abele cazuri va muta in pozitii castigatoare.
Daca un jucator este intr-o pozitie castigatoare atunci w(x) = SC sau w(x1) xor w(x2) xor ... xor w(xp) diferit de 0. In primul caz va exista un subjoc xk astfel incat w(xk) = SC. Un jucator va putea muta in acest subjoc intr-o pozitie superpierzatoare. Daca suma nim a w-numerelor subjocurilor este diferita de 0 atunci un jucator poate gasi cu usurinta o mutare care sa o modifice in 0, procedand similar jocului Nim.
Aplicatie pe jocul NIM pe nivele
Notiuni de baza | Jocul NIM | Numere Sprague-Grundy |
Adunarea jocurilor | w-numere | Aplicatii si probleme
Teoria jocurilor
(Categoria Teoria jocurilor, Autor Filip Cristian Buruiana)
- Capitole
- Notiuni de baza
- Jocul NIM
- Numere Sprague-Grundy
- Adunarea jocurilor
- w-numere
- Aplicatii si probleme
Aplicatii, probleme
In continuare vom analiza cateva aplicatii si probleme in care se aplica teoria si teoremele prezentate in capitolele precedente.
1. Game, concursul national Bursele Agora, 2004
Fie N gramezi de pietre si doi jucatori care muta alternativ. O mutare consta din alegerea unei gramezi si eliminarea unei singure pietre sau a unui numar prim de pietre din gramada aleasa. Castiga jucatorul care ia ultimele pietre. Sa se precizeze care din cei doi jucatori va castiga.
Jocul de mai sus este similar cu jocul de NIM, numai ca aici nu putem lua oricate pietre dintr-o gramada, ci doar o singura piatra sau un numar prim de pietre. Pentru a rezolva problema, facem urmatoarea observatie: jocul cu mai multe gramezi respecta proprietatile unei adunari de tip xor a jocurilor cu o singura gramada, deoarece la fiecare pas jucatorul care urmeaza trebuie sa isi aleaga exact un joc (o gramada) si sa faca o mutare in jocul respectiv. Conform teoremei, rezulta ca trebuie sa determinam valoarea mex pentru o gramada cu x pietre, si apoi sa facem suma-xor a valorilor corespunzatoare marimilor celor N gramezi. In cazul in care suma-xor este diferita de 0 va castiga jucatorul care muta primul, iar in caz contrar va castiga celalalt jucator.
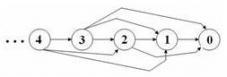 Mai ramane de calculat valoarea mex pentru o gramada cu x pietre. Putem construi un graf orientat, aciclic, in care nodul numerotat cu x, x ≥ 0, reprezinta o gramada de dimensiune x. In acest graf va exista arc de la x la y doar daca x - y este egal cu 1 sau este un numar prim. Astfel, un arc reprezinta o posibila mutare in jocul dat.
Mai ramane de calculat valoarea mex pentru o gramada cu x pietre. Putem construi un graf orientat, aciclic, in care nodul numerotat cu x, x ≥ 0, reprezinta o gramada de dimensiune x. In acest graf va exista arc de la x la y doar daca x - y este egal cu 1 sau este un numar prim. Astfel, un arc reprezinta o posibila mutare in jocul dat.
Vom incerca sa calculam valorile Sprague-Grundy corespunzatoare nodurilor acestui graf. In tabelul de mai jos sunt prezentate aceste valori pentru primele noduri ale grafului.
| nod | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SG | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | 0 | 1 | 2 |
Se poate demonstra prin inductie dupa n ca valoarea asociata nodului n este n modulo 4. Pentru 0 ≤ n ≤ 3 afirmatia este adevarata. Presupunem afirmatia adevarata pentru orice m < n. Din gramada de n obiecte pot fi luate unul, doua sau trei obiecte, deci valoarea pentru n nu poate fi niciuna din valorile pentru n-1, n-2 si n-3. Valoarea n modulo 4 este deocamdata cea mai mica valoare care nu este inca eliminata si poate corespunde gramezii cu n obiecte. Este usor de aratat ca aceasta valoare nu va fi eliminata. Presupunem prin reducere la absurd ca valoarea ar fi eliminata, deci putem alege un numar prim p de obiecte din cele n astfel incat (n-p) modulo 4 = n modulo 4, echivalent cu p modulo 4 = 0, fals, deoarece p era un numar prim. In concluzie, afirmatia pentru n este adevarata si, conform principiului inductiei matematice, este adevarata pentru orice n numar natural. In concluzie, valoarea Sprague-Grundy pentru nodul n este n modulo 4.
Coreland toate observatiile de mai sus, primul jucator castiga daca si numai daca (x1 mod 4) xor (x2 mod 4) ... xor (xN mod 4) este diferit de 0.
2. Cartonase, concursul national .campion, 2007-2008
Fie N cartonase asezate in linie dreapta pe o masa si doi jucatori care muta alternativ. Fiecare cartonas are o fata colorata in rosu, iar cealalta in albastru. O mutare consta in alegerea unui cartonas cu fata rosie in sus si intoarcerea lui. In plus, daca doreste, cel care e la mutare poate sa isi aleaga orice alt cartonas (indiferent de culoarea fetei care este in sus) care se afla la stanga celui ales initial si sa il intoarca. Stiind culorile fetelor care sunt initial in sus, sa se precizeze care jucator castiga.
Acest joc este cunoscut in literatura de specialitate ca Turning Turtles, si este de fapt echivalent cu jocul NIM, studiat in acest articol. Putem asocia unui cartonas rosu situat pe pozitia i o gramada cu i pietre in jocul NIM. Se pot observa urmatoarele:
- Starea finala din problema este cea in care nu mai exista niciun cartonas cu fata rosie in sus. Deasemenea, in jocul NIM, se ajunge in starea finala cand toate gramezile de pietre sunt vide.
- Daca un jucator intoarce un singur cartonas rosu situat pe pozitia i, mutarea lui este echivalenta cu a lua toate pietrele din gramada ce contine i pietre.
- Daca un jucator intoarce cartonasul rosu de pe pozitia i, iar apoi mai intoarce un alt cartonas de pe pozitia j (1 ≤ j < i), avem urmatoarele posibilitati:
- cartonasul de pe pozitia j este albastru: dupa ce se efectueaza mutarea, vom avea pe pozitia j un cartonas rosu, iar pe pozitia i un cartonas albastru. Aceasta mutare este echivalenta cu a lua exact i-j pietre din gramada ce contine i pietre, obtinand o gramada cu j pietre.
- cartonasul de pe pozitia j este rosu: dupa ce se efectueaza mutarea, vom aveam pe pozitiile i si j cartonase albastre, inainte acestea fiind rosii. Aceasta mutare este echivalenta cu a lua toate pietrele din gramezile ce contineau i, respectiv j pietre. Insa in jocul NIM, a lua toate pietrele din gramezile ce contin i, respectiv j pietre este echivalent cu a lua i-j pietre din gramada cu i pietre, deoarece suma-xor a numerelor de pietre din gramezi nu se schimba.
Folosindu-ne de aceste observatii, putem concluziona ca primul jucator va castiga atunci si numai atunci cand suma-xor a pozitiilor unde se afla cartonasele cu fata rosie in sus este diferita de 0.
3. A Coloring Game, concurs regional, Rusia, 2007
Fie N casute asezate in linie una dupa alta. Initial, fiecare casuta are exact una din cele trei stari posibile: necolorata, colorata in rosu, colorata in albastru. Sunt doi jucatori care muta alternativ. Prin mutare se intelege colorarea unei casute necolorate in rosu sau in albastru, astfel incat, la fiecare pas, sa nu existe doua casute adiacente colorate la fel. Sa se precizeze care jucator are strategie sigura de castig.
Pentru a rezolva aceasta problema ne vom folosi de numerele Sprague-Grundy si de teoria prezentata in capitolul Adunarea jocurilor. Se observa ca sirul initial de casute poate fi divizat in mai multe subsecvente maximale disjuncte, astfel incat fiecare subsecventa este de unul din cele 4 tipuri prezentate mai jos:
- subsecventa cu ambele capete necolorate (tip 1)
- subsecventa cu un capat colorat si cu un capat necolorat (tip 2)
- subsecventa cu ambele capete colorate la fel (tip 3)
- subsecventa cu un capat colorat in rosu, iar celalalt in albastru (tip 4)
Colorarea unei casute inseamna o mutare in jocul determinat de subsecventa careia apartine casuta. Cum la fiecare pas se alege un singur joc din cele existente si se efectueaza o singura mutare in acest joc, suntem in cazul unei adunari de tip xor a jocurilor. In consecinta, vom determina valorile Sprague-Grundy pentru fiecare joc independent in parte si vom face suma-xor a acestor valori.
Sa notam cu An valoarea Sprague-Grundy a unei secvente de lungime n de tipul 1. Similar, se noteaza cu Bn, Cn si Dn valorile pentru secvente de lungime n de tipul 2, 3 si respectiv 4. Pentru a calcula efectiv aceste valori facem toate mutarile posibile si calculam mex dintre valorile obtinute.
4. Triomino, Bytecode, 2008.
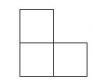 Fie o tabla cu doua linii si N coloane si doi jucatori care muta alternativ. La fiecare pas, jucatorul aflat la mutare aseaza pe tabla o piesa de forma celei din figura alaturata, astfel incat aceasta piesa sa nu se suprapuna (nici macar partial) peste alte piese deja asezate pe tabla. Atunci cand este asezata, piesa poate fi rotita cu 90, 180 sau 270 de grade. Sa se precizeze care din cei doi jucatori are strategie de castig. De exemplu, pentru N = 3, jucatorul care muta primul are strategie de castig, iar pentru N = 4 ce de-al doilea jucator are o astfel de strategie. Se cere un algoritm de complexitate O(N2).
Fie o tabla cu doua linii si N coloane si doi jucatori care muta alternativ. La fiecare pas, jucatorul aflat la mutare aseaza pe tabla o piesa de forma celei din figura alaturata, astfel incat aceasta piesa sa nu se suprapuna (nici macar partial) peste alte piese deja asezate pe tabla. Atunci cand este asezata, piesa poate fi rotita cu 90, 180 sau 270 de grade. Sa se precizeze care din cei doi jucatori are strategie de castig. De exemplu, pentru N = 3, jucatorul care muta primul are strategie de castig, iar pentru N = 4 ce de-al doilea jucator are o astfel de strategie. Se cere un algoritm de complexitate O(N2).
5. Chess Training, Topcoder, SRM 384
Aplicatie pt. WTIA
Notiuni de baza | Jocul NIM | Numere Sprague-Grundy |
Adunarea jocurilor | w-numere | Aplicatii si probleme
