Revizia anterioară Revizia următoare
Jocul NIM
Probabil cel mai cunoscut joc impartial este jocul NIM. In acest joc, se considera N gramezi, fiecare gramada avand un numar de pietre. La fiecare pas, jucatorul aflat la mutare elimina un numar nenul de pietre (eventual toate) dintr-o singura gramada. Jucatorii muta alternativ. Castigatorul este cel care ia ultimele pietre.
De obicei, jocul NIM se joaca cu 3 gramezi de pietre, insa strategia de castig este aceeasi indiferent de numarul gramezilor. Pentru a determina aceasta strategie ne vom folosi de operatia xor (exclusive or) si proprietatile ei. Aceasta operatie se realizeaza prin operatorul ^ in C/C++, si prin xor in Pascal. Ca operatie pe biti, ea poate fi interpretata ca adunare in baza 2 fara transport, dupa cum reiese din tabelul urmator:
<center>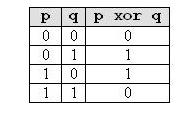
</center>
De exemplu, 1 xor 7 xor 5 = 3, deoarece avem:
1 = (001)2 xor
7 = (111)2
5 = (101)2
______________
(011)2 = 3
Pe baza operatiei xor, strategia de castig pentru NIM poate fi formulata conform urmatoarei teoreme:
Teorema: Fie N gramezi. Prima gramada are x1 pietre, cea de a doua x2, si asa mai departe, pana la ultima care are xN pietre. O astfel de pozitie este pierzatoare in jocul de NIM daca si numai daca suma-xor a numerelor de pietre din gramezi este 0, adica daca x1 xor x2 ... xor xN = 0.
Pentru a demonstra aceasta teorema, trebuie sa aratam ca dintr-o stare cu suma-xor egala cu 0 (pierzatoare), oricum am muta, nu putem ajunge decat intr-o stare cu suma-xor nenula (castigatoare), si ca dintr-o stare castigatoare putem efectua o mutare in mod convenabil astfel incat sa ajungem intr-o stare de pierdere.
Sa presupunem prin reducere la absurd ca dintr-o stare cu suma-xor 0 putem ajunge in alta stare care are suma-xor tot 0. Selectam o gramada oarecare cu y pietre si dorim sa eliminam un numar de pietre din aceasta gramada. Daca notam cu S suma-xor a numerelor de pietre din celelalte N-1 gramezi neselectate, atunci avem S xor y = 0. Dar a xor b = 0 daca si numai daca a = b, deci S = y. Daca din gramada selectata eliminam x pietre, 0 < x ≤ y, pentru a ajunge intr-o stare tot cu suma-xor 0 trebuie sa avem S xor (y-x) = 0, echivalent cu S = y-x. Din S = y rezulta ca x = 0, fals. Deci oricum am efectua o mutare dintr-o stare de pierdere vom ajunge intr-o stare castigatoare.
Ramane de demonstrat ca dintr-o stare de castig putem sa aducem adversarul intr-o stare pierzatoare. Fie S suma-xor a marimilor celor N gramezi. Daca exista o gramada cu y pietre astfel incat y ≥ y xor S, atunci putem elimina y - y xor S pietre din aceasta gramada, ramanand cu y - (y - y xor S) = y xor S pietre. Din gramada cu y pietre am obtinut o gramada cu y xor S pietre, deci noua suma-xor va fi (... xor y) xor S = S xor S = 0. Trebuie sa demonstram ca exista cel putin o gramada cu proprietatea de mai sus.
