Solutii Copii3

Ambele solutii prezentate mai jos rezolva queryurile online.

Solutia 1

Rezolvati problema pentru cazul in care, pentru fiecare query, R - L + 1 este o putere a lui 2.

timp, 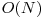memorie

Un greedy care ar rezolva corect fiecare query in parte ar fi urmatorul: Cat timp mai exista copii in interval, se alege cel a carui stramutare ar fi cat mai putin costisitoare si se muta. Astfel, fie cel mai din stanga copil din interval se va muta pe cel mai apropiat scaun liber din stanga din afara intervalului, fie cel mai din dreapta copil se va muta pe cel mai apropiat scaun liber din dreapta din afara intervalului. Pentru a calcula costul obtinut de acest algoritm, este suficient sa se mentina doua perechi de pointeri (pozitiile celui mai din stanga, respectiv din dreapta copil din interval si pozitiile celui mai apropiat scaun liber din afara intervalului in stanga, respectiv in dreapta), realizand maxim N pasi la fiecare query.

...

Solutia 2

O prima observatie impotanta (defapt aceeasi ca observatia importanta de la problema Wiring de la IOI 2017) este aceea ca, pentru un interval de query [l, r] fixat, va exista o pozitie p unde toti copii din intervalul [l, p] se dug "la stanga", si toti copii din intervalul [p+1, r] se duc "la dreapta" (caci daca aceasta nu ar exista, ar fi un copil ce se duce "la stanga" care e mai la dreapta ca un copil ce se duce "la dreapta", care e evident neoptim).
Oare putem, pentru un interval [l, r], si o pozitie p in acest interval, sa gasim "repede" care ar fi costul daca toti copii din [l, p] ar merge "la stanga", si toti copii din [p+1, r] sa mearga "la dreapta"? Sa numim aceasta valoare f(l, r, p).
Raspunsul este da: f(l, r, p) este egala cu suma pozitiilor copiilor din [l, p] minus suma pozitiilor copiilor din [p+1, r], plus suma indicilor primilor (nr. copii din [p+1, r]) spatii goale din dreapta lui r, minus suma indicilor ultimilor (nr. copii din [l, p]) spatii goale din stanga lui l. Toate valorile mentionate pot fi gasite in O(1) cu ajutorul unor precalculari usoare in O(n).
Acum, cum gasim acea pozitie optima a lui p ?
Observatia importanta este ca functia g(p) = f(l, r, pozitia celui de al p-lea copil din [l, r]) este "aproape" unimodala ; mai exact, aceasta poate avea 2 minime, dar acestea trebuie atunci sa fie adiacente. Mai mult, observam oricare valori egale in p trebuie sa fie una in stanga si una in dreapta minimului. Pentru a demonstra acest lucru, este nevoie sa observam ca, cat timp cuplam copii care merg la stanga (respectiv la dreapta) cu pozitiile goale cele mai la dreapta (respectiv la stanga) care sunt la stanga (respectiv la dreapta) lui [l, r], putem cupla oricare copil cu oricare spatiu (din comutativitate); iar astfel, arbitrar, putem alege sa cuplam al i-lea copil de la stanga (respectiv la dreapta) lui [l, r] cu al i-lea copil de la dreapta la stanga (respectiv de la stanga la dreapta) la stanga (respectiv la dreapta) lui [l, r]. Astfel, putem cauta ternar valoarea lui p (avand in vedere cazul special de egalitate). Complexitatea finala este de O(n * log(n)).

Solutia 3

/// Anybody, please...